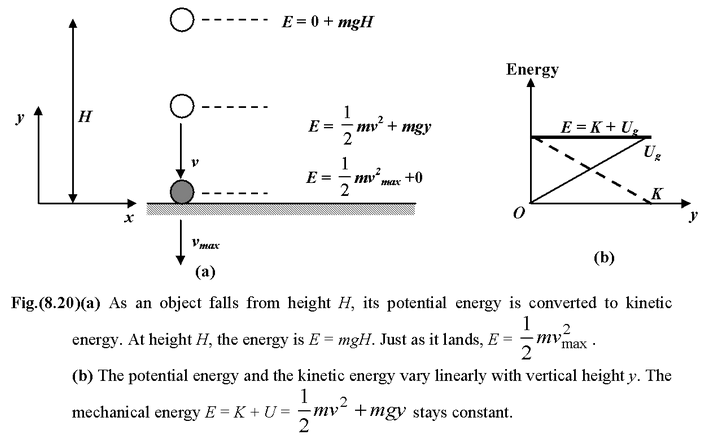
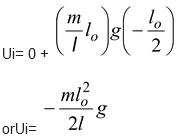Conservation of Mechanical Energy
Work Power And Energy of Class 11
From the previous section we know that the work done by a conservative force in terms of the change in potential energy is given by
ΔU = -WC(8.12)
where U is the potential energy and WCis the work done by a conservative force.
From the work-energy theorem, we know that
Wnet= ΔK
Where Wnetrepresents the sum of work done by all the forces acting on the mass.
If a particle is subject to only conservative forces, then
WC= Wnet= ΔK
Thus, the equation (8.12) becomes,
ΔU = -ΔK
orΔU + ΔK = 0 (8.14)
The equation (8.14) tells us that the total change in potential energy plus the total change in kinetic energy is zero if only conservative forces are acting on the system.
That is, there is no change in the sum of K plus U.
∴Δ(K + U) = 0 (8.15)
orΔE = 0where E = K + U
The quantity E = K + U is called the total mechanical energy.
According to equation (8.15), when only conservative forces act, the change in total mechanical energy of a system is zero, in otherwords,
If only conservative forces perform work on and within a system of masses, the total mechanical energy of the system is conserved.
Alternatively, the equation (8.15) may be written as
(Kf+ Uf) - (Ki+ Ui) = 0
orKf+ Uf= Ki+ Ui(8.16)
Since ΔE = 0, integrating both sides,
we getE = constant.
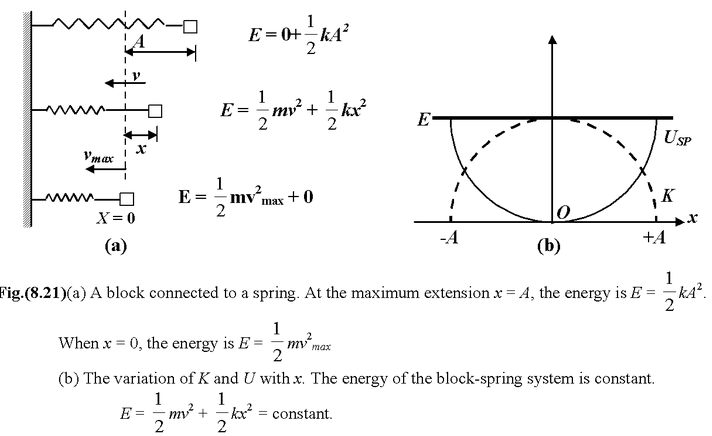
Problem Solving Strategy
1.Draw diagrams of the system showing initial and final configuration and assume a coordinate system.
2.Specify the reference level for potential energy. In case of spring, it is advisable to assume zero potential energy at the natural length of the spring. In case of gravity, any convenient level can be chosen as reference frame.
3.Looking at the initial configuration, ask yourself
What forms of energy are present?
-
if the particle is moving include
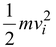
- if the particle is not located at the reference level, include mgyi
-
if the spring is stretched or compressed, include
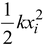
- Looking at the final configuration, ask yourself
What forms of energy are present?
-
if the particle is moving include
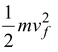
- if the particle is not located at the reference , include mgyf
-
if the spring is stretched or compressed, include
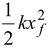
Equate the initial and final total energies
Ki+ Ui = Kf+ Uf
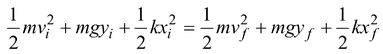
Solve for the unknown.
|
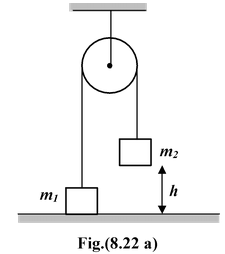
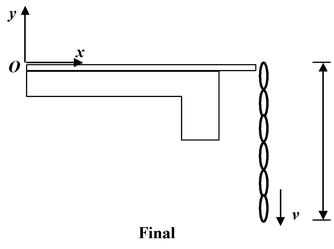
Example 8.9 Two blocks with masses m1= 3kg and m2= 5 kg are connected by a light string that slides over a frictionless pulley as shown in figure. Initially, m2 is held 5 m off the floor while m1is on the floor. The system is then released. At what speed does m2hit the floor? |
|
Solution
The initial and final configurations are shown in the figure(8.22 b&c).
It is convenient to set Ug= 0 at the floor. Initially, only m2has potential energy. As it falls, it loses potential energy and gains kinetic energy. At the same time, m1gains potential energy and kinetic energy. Just before m 2 lands, it has only kinetic energy. Let v the final speed of each mass. Then, using the law of conservation of mechanical energy.
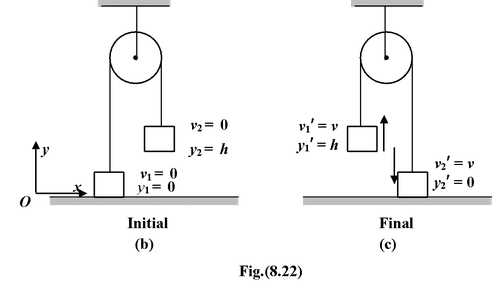
Kf + Uf= Ki+ Ui
1/2(m 1 + m 2 )v 2 + m 1 gh= 0 + m 2 gh
v
2
=
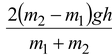
Putting m1 = 3 kg; m 2 = 5 kg; h = 5 m and g = 10 m/s 2
We get v
2
=
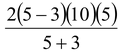
orv = 5 m/s.
Example 8.10
|
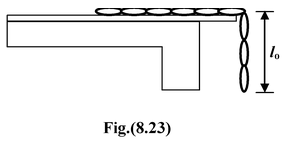
A chain of length l = 80 cm and mass
|
|
Solution
|
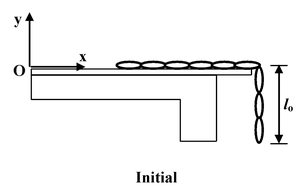
We assume the zero potential energy level at the horizontal plane. The initial and final configuration of the chain are shown in the figure. Initially, Ki= 0
|
|
|
Note that the part of chain lying over the table has zero potential energy. Finally, Kf = 1/2mv 2 Where v is the final velocity of the chain. and Uf= −1/2 mg Using the law of energy conservation Kf+ Uf= Ki+ Ui |
|
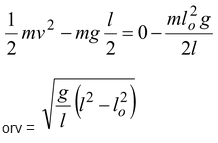
putting l = 0.8 m; lo = 0.5 m; g = 10 m/s2, we get
v = √5 m/s
orv = 2.23 m/s
Example 8.11
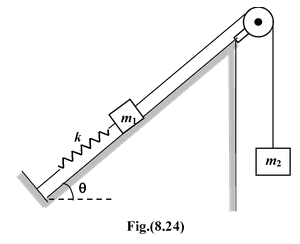
|
Two blocks with masses m
1
= 2 kg and
(a)the maximum extension of the spring (b)the speed of m1 when the extension is 0.5 m. Ignore friction and mass of the pulley. |
|
Solution
To use Ef= Eiwe would need to assign the initial heights of the blocks arbitrary values h1 and h2. The corresponding potential energies, m1gh1 and m2gh2 would appear in both Ei and Efand hence would cancel.
We avoid this process by using the form ΔK + ΔU = 0 instead, since it does not require
U = 0 reference level.
(a)At the maximum extension xmax, the blocks come to rest, and thus ΔK = 0. Next, we must find the changes in Ugand US. When m2 falls by xmax, the spring extends by xmaxand m1 rises by xmaxsinθ. Therefore,
ΔK + ΔUg + ΔUS = 0
0 + (-m 2 gx max + m1gx max sinθ) + 1/2kx 2 max = 0
Thus,xmax= 2g/k(m2 - m1 sin θ) = 0.98 m
(b)In this case the change in kinetic energy is ΔK = 1/2(m1 + m2)v2.
The change in potential energy has the same form as in part (a), but with xmaxreplaced by
x = 0.5 m,.
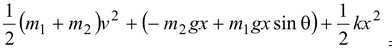 = 0
= 0
Putting the given values we find v = 1.39 m/s.
Example 8.12
|
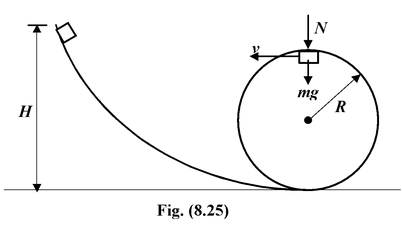
A body slides down an inclined surface which ends into a vertical loop of radius R = 40 cm. What must be the height H of the inclined surface for the body not to fall at the uppermost point of the loop? Assume friction to be absent. |
|
Solution
Let v be the velocity of the particle at the highest point.
According to Newton’s Second Law, the net force
Fnet= N + mg provides the centripetal force.
Therefore, N + mg = mv 2 /R
The body is not detached from the loop if N ≥ 0. In the limiting case, N = 0.
That is mg = mv 2 /R or v 2 = gR
Applying energy conservation at the initial and highest point of the loop, we get
mgH = mg(2R) + 1/2mv 2
Usingv 2 = gR, we obtain,
mgH = mg(2R) + 1/2m(gR)
orH = 5/2R = 2.5R
Putting R = 40 cm = 0.4 m, we get
H = (2.5) (0.4) = 1m.
Example 8.13
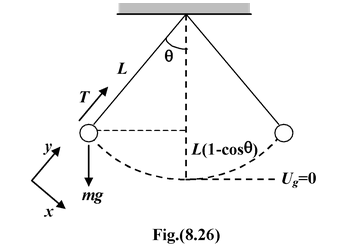
The bob of a simple pendulum of length L = 2 m has a mass m = 2 kg and a speed
v = 1 m/s when the string is at 35o to the vertical. Find the tension in the string at
(a)the lowest point in its swing
(b)the highest point
Solution
|
The problem requires to use dynamics and the conservation of mechanical energy. The forces on the bob are shown in the figure. The acceleration has both radial and tangential components. The equation for tangential component, ΣFx = mg sinθ = ma Since the bob is moving in a circular path of radius L, the equation for the radial component is |
|
ΣFy = T – mg cosθ = mv 2 /L(i)
To find the tension we need the speed, which can be found from the conservation law. We set Ug = 0 at the lowest point.
Note that the height is y = L – L cosθ. The mechanical energy is
E =
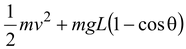 (ii)
(ii)
= 1/2 (2kg)(1 m/s) 2 + (2kg)(9.8 N/kg)(2m)(1 – 0.8) = 9 J
(a)At the lowest point θ = 0; hence (ii) becomes
E = 1/2 mv 2 max+ 0
Since E = 9 J we find vmax= 3 m/s.
Now we have the speed we can find the tension at θ = 0. From (i), T – mg = mv 2 max/L, from which we find
T = 20 + 9 = 29 N
(b)At the highest point v = 0; hence, (ii) becomes
E = 0 + mgL(1 – cosθmax)
Using E = 9 J lead to cosθmax= 31/40
Sincev = 0, therefore, T = mgcosθmax = 15.5 N
|
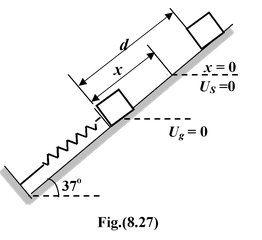
Example 8.14 A block of mass m = 0.2 kg is held against, but not attached to a spring (k = 50 N/m) which is compressed by 20 cm, as shown in figure, when the block is released, the block slides 50 cm up the rough incline before coming to rest. Find (a)the force of friction (b)the speed of the block as it leaves the spring. |
|
Solution
We could set Ug= 0 at x = 0, but if we use the lowest point instead, all subsequent values are positive. Again the total energy has three terms E = K + Ug+ US.
(a)We set xo= 0.2 m and d = 0.5 m. Both Kiand Kfare zero, so Ei=
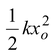 and Ef= mgdsinθ. From work-energy theorem,
and Ef= mgdsinθ. From work-energy theorem,
Ef– Ei= Wnc
mgdsinθ -
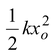 = -fd
= -fd
Thus f = 0.82 N
(b)The initial energy Eiis the same as above, but the final value at x = 0 is
Ef =
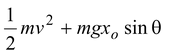
From work-energy theorem,
Ef– Ei= Wnc
1/2 mv 2 + mgxosinθ - 1/2 kxo 2 = - fxo
After solving we get, v = 2.45 m/s.