Electric Field Formula - Definition, Solved Examples, Relation With V
Electric Field Formula: The electric field at a specific point in space is defined as the force (F) experienced by a positive test charge (q) placed at that point, divided by the magnitude of the test charge.
Murtaza Mushtaq11 Oct, 2023
Share
Electric Field Formula: The electric field (E) at a point in space is defined as the force (F) experienced by a positive test charge (q) placed at that point, divided by the magnitude of the test charge.
Mathematically, it can be expressed as:
E = F / q
Where:
- E is the electric field.
- F is the force experienced by the test charge.
- q is the magnitude of the test charge.
Certainly, let's provide an explanation of the electric field in terms of electric potential (V).
Also Check - Shear Modulus Formula
Electric Field in Terms of Electric Potential (V)
Electric Field Formula: The electric field (E) and electric potential (V) are closely related concepts in electromagnetism. Electric potential, often referred to as voltage, represents the electric potential energy per unit charge at a point in space. Electric field, on the other hand, describes the force experienced by a test charge at that point. The relationship between electric field and electric potential can be expressed as follows:E = -∇V
Where:
- E is the electric field vector. - ∇ (pronounced "nabla") is the del operator, representing the gradient. - V is the electric potential (voltage). In this equation, the negative sign indicates that the electric field points in the direction of steepest decrease in electric potential. In simpler terms, the electric field tells us the direction in which a positive test charge would move if placed in the electric potential field. To put it even more simply, think of electric potential (V) as a hill or slope, where the height of the hill represents the potential energy. The electric field (E) is like the slope of the hill. A positive test charge placed on the hill will roll down the slope in the direction of the steepest descent, which is the direction of the electric field. So, when working with electric potential (V), keep in mind that the electric field (E) is the "slope" or gradient of the potential, and it indicates the direction and magnitude of the force experienced by a charged particle placed in that field. This relationship between electric field and electric potential is a fundamental concept in electromagnetism and is widely used to analyze and understand electric fields in various practical applications, including circuit analysis and the behavior of charged particles in electric fields.Also Check - Soil Erosion Formula
Solved Examples of Electric Field Formula
Example 1: Calculating the Electric Field Due to a Point ChargeLet's consider a point charge Q = 5 μC placed at a distance of r = 2 meters from a test charge q = 1 μC. Calculate the electric field at this point.
Solution:
Using Coulomb's Law, we can find the force between these charges: F = (k * |Q * q|) / r²Where:
- k is Coulomb's constant (8.99 × 10^9 N m²/C²). F = (8.99 × 10^9 N m²/C² * |5 μC * 1 μC|) / (2 m)² F = (44.95 N m²/C²) / 4 m² F = 11.24 N/C Now, we can find the electric field using the formula E = F / q: E = 11.24 N/C / 1 μC E = 11.24 × 10^6 N/C So, the electric field at this point is 11.24 × 10^6 N/C.Also Check - Efficiency Formula
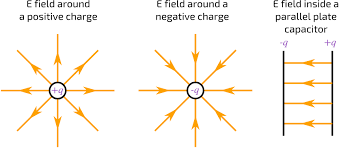
Example 2: Electric Field Between Two Parallel PlatesConsider two parallel plates with a potential difference of 100 V and a separation of 0.02 meters. Calculate the electric field between the plates.
Solution:
The electric field between parallel plates is given by: E = V / dWhere:
- V is the potential difference. - d is the separation between the plates. E = 100 V / 0.02 m E = 5000 N/C The electric field between the plates is 5000 N/C.Applications of Electric Field Formula
Electric fields find numerous applications in our daily lives and various fields of science and technology. Some notable applications include:- Electrostatic Precipitators: Used to remove dust and pollutants from industrial emissions.
- Capacitors: Essential components in electronic circuits.
- Particle Accelerators: Employed in research to accelerate charged particles.
- Electric Motors: Convert electrical energy into mechanical energy.
- Electrocardiograms (ECGs): Measure the electrical activity of the heart.
Electric Field Formula FAQs
What is the unit of electric field?
The unit of electric field is N/C (Newtons per Coulomb).
Can the electric field be negative?
Yes, the electric field can be negative, indicating a force in the opposite direction of a positive test charge.
What is the significance of electric field lines?
Electric field lines provide a visual representation of the electric field's direction and strength.
How does the electric field differ from the gravitational field?
The electric field is associated with electric charges, while the gravitational field is associated with mass. Both fields follow inverse-square laws.
What is Gauss's Law, and how is it related to electric fields?
Gauss's Law relates the electric flux through a closed surface to the net charge enclosed within the surface. It's a fundamental principle in electromagnetism.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.