Shear Modulus Formula: Definition, Types and Solved Examples

Shear Modulus, denoted as G , also known as the modulus of rigidity, is a material property that quantifies its resistance to deformation when subjected to shearing forces.

What is Shear Modulus?

Shear modulus (G), also referred to as the modulus of rigidity, is a measure of a material's ability to resist deformation when subjected to shearing forces. Shearing forces are forces that act parallel to a surface, causing one layer of the material to shift with respect to an adjacent layer. In essence, shear modulus quantifies the material's stiffness under shear stress.

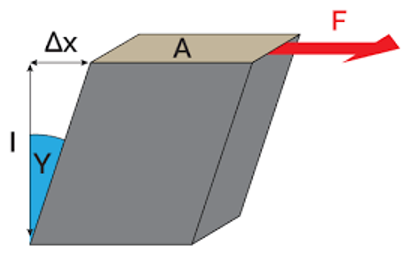
Modulus of Rigidity Formula

The shear modulus (G) is calculated using the following formula:

G = (F / A) * (L / Δx)

Where:

- G is the shear modulus (modulus of rigidity).

- F is the shearing force applied to the material.

- A is the cross-sectional area over which the shearing force is applied.

- L is the original length of the material.

- Δx is the amount by which the material is displaced.

Modulus of Rigidity – Overview

Modulus of rigidity is an essential parameter in material science and engineering. It helps determine how materials respond to shearing forces and is particularly important in the design of structures and materials used in torsional applications.

Also Check – Unit, Dimension & Vector Formula

Example of Modulus of Rigidity

Let's work through an example to calculate the shear modulus for a given material:

Example 3: Shear Modulus Calculation for Aluminum

Properties:

- Shearing force (F): 8000 N

- Cross-sectional area (A): 0.015 m²

- Original length (L): 3 m

- Displacement (Δx): 0.002 m

Use the shear modulus formula:

G = (F / A) * (L / Δx)

Substitute the values:

G = (8000 N / 0.015 m²) * (3 m / 0.002 m)

Calculating:

G = 26,666.67 N/m² = 26.67 kPa

The shear modulus (G) for the aluminum specimen is approximately 26.67 kilopascals (kPa).

Also Check – Work Done in Raising a Box Formula

Solved Examples on Shear Modulus Formula

Example 1: Shear Modulus Calculation for Steel

Properties:

- Shearing force (F): 10,000 N

- Cross-sectional area (A): 0.01 m²

- Original length (L): 2 m

- Displacement (Δx): 0.001 m

Use the shear modulus formula:

G = (F / A) * (L / Δx)

Substitute the values:

G = (10,000 N / 0.01 m²) * (2 m / 0.001 m)

Calculating:

G = 20,000,000 N/m² = 20 MPa

The shear modulus (G) for the steel bar is 20 megapascals (MPa).

Example 2: Shear Modulus Calculation for Rubber

Properties:

- Shearing force (F): 500 N

- Cross-sectional area (A): 0.02 m²

- Original length (L): 1 m

- Displacement (Δx): 0.005 m

Use the shear modulus formula:

G = (F / A) * (L / Δx)

Substitute the values:

G = (500 N / 0.02 m²) * (1 m / 0.005 m)

Calculating:

G = 500,000 N/m² = 500 kPa

Also Check – Work Done by a Variable Force Formula

Applications

Certainly! Here are 20 applications of shear modulus (\(G\)) along with brief descriptions for each:

1. Building Design: Engineers use shear modulus to calculate how materials like concrete and steel withstand lateral loads in building structures, ensuring stability during seismic events.
2. Aircraft Design: Shear modulus helps design aircraft components to withstand shear stresses during flight, ensuring safety and structural integrity.
3. Automotive Suspensions: Car manufacturers consider shear modulus when designing suspensions to provide comfort and control, minimizing lateral movements during cornering.
4. Oil Well Drilling: In the oil industry, shear modulus is used to analyze drilling mud properties and ensure drilling stability in various geological formations.
5. Torsion Springs: Shear modulus is crucial in designing torsion springs, which store and release energy by twisting, commonly used in doors and mechanical systems.
6. Rubber Products: Manufacturers of rubber products use shear modulus to determine the material's resistance to shear forces, ensuring product durability and flexibility.
7. Elasticity of Textiles: The textile industry employs shear modulus to assess the elasticity of fabrics and materials used in clothing and textiles.
8. Biomechanics: Researchers use shear modulus to study the mechanical properties of soft tissues and understand their behavior in the human body.
9. Bridge Design: Civil engineers apply shear modulus to design bridge components, considering shear forces from traffic loads and environmental factors.
10. Geological Studies: Geologists use shear modulus to analyze the behavior of rocks and soils under different stress conditions, aiding in geological studies.
11. Material Testing: Shear modulus is measured during material testing to characterize the stiffness of materials and predict their performance in various applications.
12. Tire Manufacturing: In the tire industry, shear modulus is a key factor in designing tire compounds that provide grip and stability on road surfaces.
13. Sports Equipment: Manufacturers of sports equipment use shear modulus to design products like tennis rackets, golf club shafts, and ski poles for optimal performance.
14. Structural Analysis: Engineers use shear modulus in finite element analysis to simulate the behavior of structures under various loads and conditions.
15. Manufacturing Processes: In manufacturing, shear modulus helps optimize processes like metal forming and forging to ensure product quality and integrity.
16. Sound Damping: Shear modulus is considered in designing materials for soundproofing and vibration damping applications in buildings and vehicles.
17. Electronic Packaging: Shear modulus is used in electronic packaging to ensure that materials can withstand the stresses and vibrations within electronic devices.
18. Aerospace Engineering: Aerospace engineers utilize shear modulus to design components for spacecraft and aircraft, ensuring their ability to withstand flight conditions.
19. Dental Materials: In dentistry, shear modulus is used to evaluate the mechanical properties of dental materials like crowns, bridges, and braces.
20. Material Selection: Engineers and scientists use shear modulus as a criterion for material selection in various industries, ensuring that materials meet specific performance requirements.

These applications demonstrate the versatility and importance of shear modulus in diverse fields, from engineering and construction to medical research and manufacturing.