Gay Lussac's Law Formula: Gay Lussac's Law, a fundamental principle among the Ideal Gas Laws, establishes a connection between a gas's pressure and its absolute temperature when maintaining a constant volume. At its core, Gay Lussac's Law posits that the pressure generated by a gas exhibits a direct correlation with its temperature, as long as mass and volume remain unchanged. This scientific principle, bearing the name of the 19th-century French chemist Joseph Gay-Lussac, who first articulated it in 1808, boasts a wide array of applications across scientific disciplines and everyday scenarios.
Also Check –
Partial Pressure Formula
What Constitutes Gay-Lussac's Law?
Gay Lussac's Law succinctly states that, assuming a constant volume, the pressure exerted by a gas is directly proportional to the gas's absolute temperature. Put differently, the pressure exerted by a gas displays proportionality to its temperature while the volume remains unaltered, expressed mathematically as:
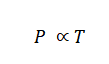
By introducing a proportionality constant, denoted as "k," the relationship can be represented as:
P = kT
Now, let's consider two scenarios: one at temperature T 1 with pressure P 1 , and another at temperature T 2 with pressure P 2 . We can express these situations using equations (1) and (2), respectively:
P 1 =kT 1 (1)
P 2 =kT 2 (2)
Combining equations (1) and (2) yields:
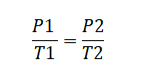
Here, "P" represents the gas's pressure, while "T" signifies the absolute temperature of the gas.
Also Check –
Bleaching Powder Formula
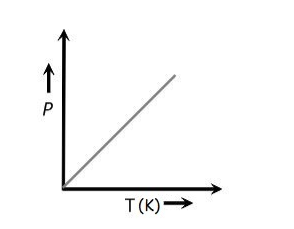
Gay Lussac's Law Illustrated Graphically
Gay Lussac's Law can be visualized through the equation:
P=kT —--------(1)
From a mathematical standpoint, this equation bears resemblance to the linear equation y=mx represented by equation (2), where "y" corresponds to "P," "m" is analogous to "k," and "x" aligns with "T." Consequently, the graph depicting this equation adopts a linear form.
Gay Lussac's Law Derivation
The formula encapsulating Gay-Lussac's Law is articulated as:
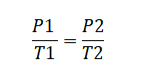
Here, P 1 signifies the initial pressure, T 1 represents the initial temperature, P 2 denotes the final pressure, and T 2 signifies the final temperature.
To derive Gay-Lussac's Law, we commence with the understanding that gas pressure is proportional to its temperature. This relationship can be symbolized as:
Substituting the proportionality sign with the constant "k," we attain:
P=kT
This equation holds true across all values of pressure and temperature.
Let's assume a scenario where a gas exerts pressure P 1 at temperature T 1 . We can express this situation as:
P 1 =kT 1
By rearranging this equation, we find:
k= T 1 P 1 —-------------(1)
Subsequently, as the gas's temperature changes to T 2 and its pressure shifts to P 2 , this transformation can be articulated as:
P 2 =kT 2
Again, rearranging the equation yields:
k= T 2 P 2 —------------(2)
Now, by equating equations (1) and (2), we arrive at:
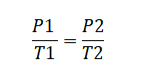
This derivation solidifies the scientific underpinning of Gay Lussac's Law.
Also Check –
Chemical Bonding Formula
Gay Lussac's Law of Gaseous Volumes
In addition to the law bearing his name, Joseph Louis Gay-Lussac introduced the concept of the Law of Gaseous Volumes in 1808. Distinguished from the Law of Definite Proportions, Gay Lussac's Law of Gaseous Volumes asserts that, when measured under identical temperature and pressure conditions, the ratios of volumes for reacting gases consist of small whole numbers. It's important to note that while the Law of Definite Proportions relates to a gas's mass, Gay Lussac's Law of Gaseous Volumes pertains to its volume.
Examples Illustrating Gay Lussac's Law
Gay Lussac's Law finds practical application in various aspects of our daily lives. A few instances include:
Pressure Cooker Efficiency: Increasing the heat applied to a pressure cooker leads to elevated pressure within, resulting in reduced cooking time. This sealed environment prevents steam from losing the food's flavor to the surrounding air
Tire Pressure Fluctuations: In vehicle tires, excessive air during hot weather can lead to over-pressurization, while colder temperatures can cause pressure reduction, resulting in underinflated tires.
Aerosol Can Safety: Storing aerosol cans in high-temperature environments is discouraged because elevated temperatures increase the pressure inside the can, potentially leading to dangerous explosions.
Gay Lussac's Law Formula Solved Examples
Example 1:
A gas in a sealed container has an initial pressure of 3 atm at a temperature of 25°C. If the temperature is raised to 75°C while keeping the volume constant, what will be the final pressure?
Solution: Given values: Initial Pressure (P1) = 3 atm Initial Temperature (T1) = 25°C = 298 K (convert to Kelvin) Final Temperature (T2) = 75°C = 348 K
Using the formula:
P1/T1=P2/T2
Substituting the values:
3/298=P2/348
Solving for P2:
P2=(3∗348)/298
P2≈3.49atm The final pressure (P2) is approximately 3.49 atm.
Example 5:
In a gas cylinder, the initial pressure is 10 kPa at a temperature of 20°C. If the pressure decreases to 5 kPa while the temperature remains constant, what is the new temperature in Celsius?
Solution:
Given values: Initial Pressure (P1) = 10 kPa
Initial Temperature (T1) = 20°C
Final Pressure (P2) = 5 kPa
Using the formula:
P1/T1=P2/T2
Substituting the values:
10/(20+273)=5/T2
Solving for T2:
T2=(5∗(20+273))/10
T2≈293K Converting back to Celsius:
T2≈293−273
T2≈20°C
The new temperature (T2) in Celsius is approximately 20°C.
