ICSE Class 10 Maths Selina Solutions Chapter 16 Loci
Neha Tanna22 Jul, 2024
Share
ICSE Class 10 Maths Selina Solutions Chapter 16: A locus is a moving point that satisfies one or more stated conditions by following a path. This ICSE Class 10 Maths Selina Solutions Chapter 16 covers symmetry-based theorems, their applications, and their constructions.
The finest resource available to pupils looking for an after-school reference to solve practice problems is Selina Solutions for Class 10 Mathematics. Our subject matter specialists have prepared all of the solutions, taking into account the most recent ICSE marking patterns.ICSE Class 10 Maths Selina Solutions Chapter 16 Loci Overview
ICSE Class 10 Maths Selina Solutions Chapter 16 on Loci are a helpful guide for students learning about geometric loci. This chapter explores how to define and understand loci, which are sets of points that satisfy certain conditions. The ICSE Class 10 Maths Selina Solutions Chapter 16 provided are clear and detailed, offering step-by-step explanations for solving problems related to loci. They include a variety of practice exercises that cover different types of loci, helping students to develop strong problem-solving skills. These ICSE Class 10 Maths Selina Solutions Chapter 16 are designed to support students in mastering the concepts effectively and preparing well for their exams by ensuring thorough understanding and practice.ICSE Class 10 Maths Selina Solutions Chapter 16 PDF
Below we have provided ICSE Class 10 Maths Selina Solutions Chapter 16 in detail. This chapter will help you to clear all your doubts regarding the chapter Inequalities. Students are advised to prepare from these ICSE Class 10 Maths Selina Solutions Chapter 16 before the examinations to perform better.ICSE Class 10 Maths Selina Solutions Chapter 16 PDF
ICSE Class 10 Maths Selina Solutions Chapter 16 Exercise 16A
Below we have provided ICSE Class 10 Maths Selina Solutions Chapter 16 –1. Given: PQ is a perpendicular bisector of side AB of the triangle ABC.
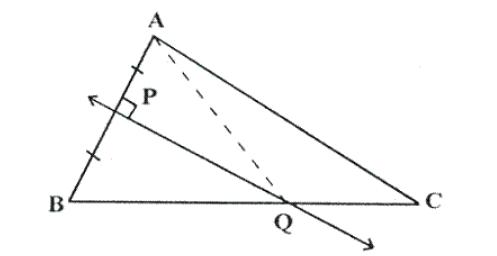
Solution:
Construction: Join AQ Proof: In ∆AQP and ∆BQP, AP = BP [Given] ∠QPA = ∠QPB [Each 90 o ] PQ = PQ [Common] Thus, by SAS criterion of congruence ∆AQP ≅ ∆BQP And, by Corresponding Parts of Congruent Triangle (CPCT) AQ = BQ Therefore, Q is equidistant from A and B.2. Given: CP is the bisector of angle C of ∆ABC
Prove: P is equidistant from AC and BC.
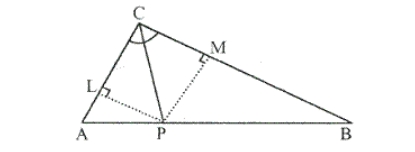
Solution:
Construction: From P, draw PL ⊥ AC and PM ⊥ CB Proof: In ∆LPC and ∆MPC, ∠PLC = ∠PMC [Each 90 o ] ∠PCL = ∠MCP [Given] PC = PC [Common] Thus, by AAS criterion of congruence ∆LPC ≅ ∆MPC And, by Corresponding Parts of Congruent Triangle (CPCT) PL = PM Therefore, P is equidistant from AC and BC.3. Given: AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y.
Prove:
i) X is equidistant from AB and AC.
ii) Y is equidistant from A and C
Solution:
From X, draw XL ⊥ AC and XM ⊥ AB. And, join YC Proof: (i) In ∆AXL and ∆AXM, ∠XAL = ∠XAM [Given] AX = AX [Common] ∠XLA = ∠XMA [Each 90 o ] Thus, by ASA criterion of congruence ∆AXL ≅ ∆AXM And, by Corresponding Parts of Congruent Triangle (CPCT) XL = XM Therefore, X is equidistant from AC and AB. (ii) In ∆YTA and ∆YTC, AT = CT [because PQ is perpendicular bisector of AC] ∠YTA = ∠YTC [Each 90 o ] YT = YT [Common] Thus, by SAS criterion of congruence ∆YTA ≅ ∆YTC And, by Corresponding Parts of Congruent Triangle (CPCT) YA = YC Therefore, Y is equidistant from A and C.4. Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
Solution:
Given: In triangle ABC, AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm Steps of Construction: i) Draw a line segment BC = 6.3 cm ii) With centre B and radius 4.2 cm, draw an arc. iii) With centre C and radius 5 cm, draw another arc which intersects the first arc at A. iv) Join AB and AC. Then, ∆ABC is the required triangle. v) Again with centre B and C and radius greater than ½ BC, draw arcs which intersects each other at L and M. vi) Join LM intersecting AC at D and BC at E. vii) Join DB. Proof: In ∆DBE and ∆DCE, BE = EC [LM is the bisector of BC] ∠DEB = ∠DEC [Each 90 o ] DE = DE [Common] Thus, by SAS criterion of congruence ∆DBE ≅ ∆DCE And, by Corresponding Parts of Congruent Triangle (CPCT) DB = DC Therefore, D is equidistant from B and C.5. In each of the given figures: PA = PB and QA = QB
(i)
Prove in each case, that PQ (produced, if required) is perpendicular bisector of AB.
Hence, state the locus of the points equidistant from two given fixed points.
Solution:
Construction: Join PQ which meets AB in D. Proof: As P is equidistant from A and B. Thus, P lies on the perpendicular bisector of AB. Similarly, as Q is equidistant from A and B. Q lies on perpendicular bisector of AB. Thus, both P and Q lie on the perpendicular bisector of AB. Therefore, PQ is the perpendicular bisector of AB. Hence, locus of the points which are equidistant from two fixed points, is a perpendicular bisector of the line joining the fixed points.6. Construct a right angled triangle PQR, in which ∠Q = 90 o , hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meet PR at point T. Prove that T is equidistant from PQ and QR.
Solution:
Steps of Construction: i) Draw a line segment QR = 4.5 cm ii) At Q, draw a ray QX making an angle of 90 o iii) With centre R and radius 8 cm, draw an arc which intersects QX at P. iv) Join RP. ∆PQR is the required triangle. v) Draw the bisector of ∠PQR which meets PR at T. vi) From T, draw perpendicular TL and TM respectively on PQ and QR. Proof: In ∆LTQ and ∆MTQ ∠TLQ = ∠TMQ [Each 90 o ] ∠LQT = ∠TQM [QT is angle bisector] QT = QT [Common] Thus, by AAS criterion of congruence ∆LTQ ≅ ∆MTQ And, by Corresponding Parts of Congruent Triangle (CPCT) TL = TM Therefore, T is equidistant from PQ and QR.7. Construct a triangle ABC in which angle ABC = 75 o , AB = 5cm and BC = 6.4 cm. Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisectors intersect each other at point P; prove that P is equidistant from B and C; and also from AC and BC.
Solution:
Steps of Construction: i) Draw a line segment BC = 6.4 cm ii) At B, draw a ray BX making an angle of 75 o with BC and cut off BA = 5 cm. iii) Join AC. ∆ABC is the required triangle. iv) Draw the perpendicular bisector of BC. v) Draw the angle bisector of angle ACB which intersects the perpendicular bisector of BC at P. vi) Join PB and draw PL ⊥ AC. Proof: In ∆PBQ and ∆PCQ, PQ = PQ [Common] ∠PQB = ∠PQC [Each 90 o ] BQ = QC [PQ is the perpendicular bisector of BC] Thus, by SAS criterion of congruence ∆PBQ ≅ ∆PCQ And, by Corresponding Parts of Congruent Triangle (CPCT) PB = PC Therefore, P is equidistant from B and C. Also, In ∆PQC and ∆PLC, ∠PQC = ∠PLC [Each 90 o ] ∠PCQ = ∠PCL [Given] PC = PC [Common] Thus, by AAS criterion of congruence ∆PQC ≅ ∆PLC And, by Corresponding Parts of Congruent Triangle (CPCT) PQ = PL Therefore, P is equidistant from AC and BC.8. In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B. Prove that P is equidistant from AB and BC.
Solution:
Construction: From P, draw PL ⊥ AB and PM ⊥ BC Proof: In ∆PLB and ∆PMB, ∠PLB = ∠PMB [Each 90 o ] ∠PBL = ∠PBM [Given] PB = PB [Common] Thus, by AAS criterion of congruence ∆PLB ≅ ∆PMB And, by Corresponding Parts of Congruent Triangle (CPCT) PL = PM Therefore, P is equidistant from AB and BC.9. In triangle LMN, bisectors of interior angles at L and N intersect each other at point A.
Prove that:
i) point A is equidistant from all the three sides of the triangle.
ii) AM bisects angle LMN.
Solution:
Construction: Join AM Proof: (i) Since, A lies on bisector of ∠N So, A is equidistant from MN and LN. Again, as A lies on the bisector of ∠L A is equidistant from LN and LM. Therefore, A is equidistant from all three sides of the triangle LMN. And, (ii) As A lies on the bisector of ∠M. Hence, AM bisects ∠LMN10. Use ruler and compasses only for this question.
(i) Construct ∆ABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60 o
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
Solution:
Steps of construction: (i) Draw line BC = 6 cm and construct angle CBX = 60 o . Cut off AB = 3.5. Join AC, triangle ABC is the required triangle. (ii) Draw the perpendicular bisector of BC and bisector of angle B. (iii) Now, bisector of angle B meets bisector of BC at P. Hence, BP is the required length, where PB = 3.5 cm. (iv) P is the point which is equidistant from BA and BC, which is also equidistant from B and C. PB = 3.5 cmICSE Class 10 Maths Selina Solutions Chapter 16 Exercise 16B
Describe the locus for questions 1 to 13 given below:
1. The locus of a point at a distance of 3 cm from a fixed point.
Solution:
The locus of a point which is at a distance of 3 cm away from a fixed point is circumference of a circle whose radius is 3 cm and the fixed point is the centre of the circle.2. The locus of a points at a distance of 2 cm from a fixed line.
Solution:
The locus of points which are at a distance of 2 cm from a fixed line AB are a pair of straight lines l and m which are parallel to the given line at a distance of 2 cm.
3. The locus of the centre of a wheel of a bicycle going straight along a level road.
Solution:
The locus of the centre of a wheel, which is going straight along a level road will be a straight line parallel to the road at a distance equal to the radius of the wheel.4. The locus of the moving end of the minute hand of a clock.
Solution:
The locus of the moving end of the minute hand of the clock will be a circle whose radius will be the length of the minute hand.5. The locus of a stone dropped from the top of a tower.
Solution:
The locus of a stone which is dropped from the top of a tower will be a vertical line through the point from which the stone is dropped.
6. The locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.
Solution:
The locus of the runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge will be the circumference of a circle where the radius is equal to the radius of the inner circular track and exceeding 1.5 m.7. The locus of the door-handle, as the door opens.
Solution:
The locus of the door handle will be the circumference of a circle with centre at the axis of rotation of the door and the radius equal to distance between the door handle and the axis of rotation of the door.8. The locus of a points inside a circle and equidistant from two fixed points on the circumference of the circle.
Solution:
The locus of the points inside the circle which are equidistant from the fixed points on the circumference of a circle will be a diameter which is the perpendicular bisector of the line joining the two fixed points on the circle.9. The locus of the centres of all circles passing through two fixed points.
Solution:
The locus of the centres of all the circles passing through two fixed points will be the perpendicular bisector of the line segment joining the two given fixed points.10. The locus of vertices of all isosceles triangles having a common base.
Solution:
The locus of vertices of all isosceles triangles having a common base will be the perpendicular bisector of the common base of the triangles.11. The locus of a point in space which is always at a distance of 4 cm from a fixed point.
Solution:
The locus of a point in space is the surface of the sphere whose centre is the fixed point and radius equal to 4 cm.12. The locus of a point P, so that:
AB 2 = AP 2 + BP 2 ,
where A and B are two fixed points.
Solution:
The locus of the point P is the circumference of a circle with AB as diameter and satisfies the condition AB 2 = AP 2 + BP 2 .13. The locus of a point in rhombus ABCD, so that it is equidistant from
i) AB and BC; ii) B and D.
Solution:
i) The locus of the point in a rhombus ABCD which is equidistant from AB and BC will be the diagonal BD of the rhombus. The locus of the point in a rhombus ABCD which is equidistant from B and D will be the diagonal AC.14. The speed of sound is 332 meters per second. A gun is fired. Describe the locus of all the people on the Earth’s surface, who hear the sound exactly one second later.
Solution:
The locus of all the people on Earth’s surface is the circumference of a circle whose radius is 332 m and centre is the point where the gun is fired.15. Describe:
i) The locus of points at distances less than 3 cm from a given point.
ii) The locus of points at distances greater than 4 cm from a given point.
iii) The locus of points at distances less than or equal to 2.5 cm from a given point.
iv) The locus of points at distances greater than or equal to 35 mm from a given point.
v) The locus of the centre of a given circle which rolls around the outside of a second circle and is always touching it.
vi) The locus of the centres of all circles that are tangent to both the arms of a given angle.
vii) The locus of the mid-points of all chords parallel to a given chord of a circle.
viii) The locus of points within a circle that are equidistant from the end points of a given chord.
Solution:
i) The locus of the points will be the space inside of the circle whose radius is 3 cm and centre as the given point. ii) The locus of the points will be the space outside of the circle whose radius is 4 cm and centre is the given fixed point. iii) The locus of points is the space inside and the circumference of the circle with a radius of 2.5 cm and the centre as the given fixed point. iv) The locus is the space outside and circumference of the circle with a radius of 35 mm and the centre as the given fixed point. v) The locus is the circumference of the circle concentric with the second circle whose radius is equal to the sum of the radii of the given two circles. vi) The locus of the centre of all circles whose tangents are the arms of a given angle is the bisector of that angle. vii) The locus of the mid-points of the chords which are parallel to a given chords is the diameter perpendicular to the given chords. viii) The locus of the points within a circle which are equidistant from the end points of a given chord is the diameter which is the perpendicular bisector to the given chord.Benefits of ICSE Class 10 Maths Selina Solutions Chapter 16
ICSE Class 10 Maths Selina Solutions Chapter 16 FAQs
Which is the hardest chapter of class 10 maths?
Which is the most important chapter in maths class 10 ICSE?
Does ICSE give grace marks?
Does ICSE give marks for attempting questions?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
