ICSE Class 10 Maths Selina Solutions Chapter 19 Constructions
Neha Tanna25 Jul, 2024
Share
ICSE Class 10 Maths Selina Solutions Chapter 19: Students will learn how to construct tangents to a given circle, circumscribed and inscribed circles on a triangle, and circumscribed and inscribed circles on regular hexagons in this chapter.
Since this chapter of the ICSE is expected to have at least one question, you must comprehend these constructs. Therefore, students can consult Selina Solutions for Class 10 Mathematics if they are experiencing trouble understanding any chapter in Concise Mathematics Selina.ICSE Class 10 Maths Selina Solutions Chapter 19 Overview
Chapter 19 of ICSE Class 10 Maths Selina Solutions covers constructions in geometry, teaching students how to draw accurate geometric figures using basic tools like a compass and ruler. The chapter begins with fundamental constructions of lines, angles, and triangles, progressing to more complex figures like quadrilaterals and circles. Each construction is explained step-by-step with clear instructions and diagrams, ensuring students grasp the concepts thoroughly. The goal of this chapter is to equip students with essential skills in geometric constructions, which are not only important for theoretical knowledge but also for practical applications in various fields. By learning these techniques, students can accurately draw geometric shapes based on given conditions such as side lengths, angles, and relationships between figures. This chapter also emphasizes the importance of precision and understanding geometric principles, laying a strong foundation for further studies in mathematics and related disciplines.ICSE Class 10 Maths Selina Solutions Chapter 19 PDF
Below we have provided ICSE Class 10 Maths Selina Solutions Chapter 19 in detail. This chapter will help you to clear all your doubts regarding the chapter. Students are advised to prepare from these ICSE Class 10 Maths Selina Solutions Chapter 19 before the examinations to perform better.ICSE Class 10 Maths Selina Solutions Chapter 19 PDF
ICSE Class 10 Maths Selina Solutions Chapter 19
Below we have provided ICSE Class 10 Maths Selina Solutions Chapter 19. Students are advised to thoroughly practice these ICSE Class 10 Maths Selina Solutions Chapter 19 –1. Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
Solution:
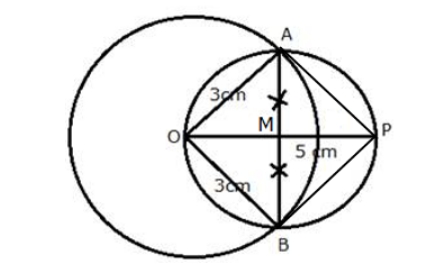Steps of construction:
i) Draw a circle with centre O and radius 3 cm.
ii) Take a point P from O, such that OP = 5 cm.
iii) Now, draw a bisector of OP which intersects OP at M.
iv) With centre M, and radius OM, draw a circle which intersects the given circle at A and B.
v) Join AP and BP.
Thus, AP and BP are the required tangents.
On measuring, we get AP = BP = 4 cm.
2. Draw a circle of diameter of 9 cm. Mark a point at a distance of 7.5 cm from the centre of the circle. Draw tangents to the given circle from this exterior point. Measure the length of each tangent.
Solution:
Steps of construction: i) Taking O as the centre, draw a circle of diameter 9 cm (radius = 4.5 cm). ii) Mark a point P outside the circle, such that PO = 7.5 cm. iii) Taking OP as the diameter, draw a circle such that it cuts the earlier circle at A and B. iv) Now, join PA and PB. Hence, PA and PB are required tangents. On measuring, we get PA = PB = 6 cm.3. Draw a circle of radius 5 cm. Draw two tangents to this circle so that the angle between the tangents is 45º.
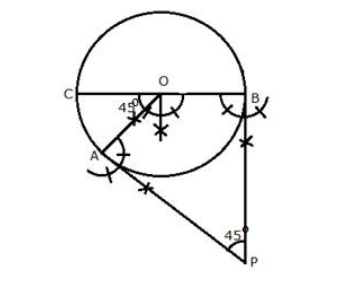
Solution:
Steps of construction: i) With centre O, draw a circle with radius BC = 5 cm ii) Draw arcs making an angle of 180º – 45º = 135º at O such that ∠AOB = 135º iii) At A and B, draw two rays making an angle of 90º at each point which meet each other at point P, outside the circle. iv) Then, AP and BP are the required tangents which make an angle of 45º with each other at P.4. Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60º.
Solution:
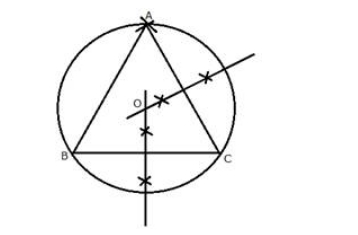Steps of Construction:
i) With centre O, draw a circle with radius BC = 4.5 cm
ii) Draw arcs making an angle of 180º – 60º = 120º at O such that ∠AOB = 120º
iii) At A and B, draw two rays making an angle of 90º at each point which meet each other at point P, outside the circle.
iv) Then, AP and BP are the required tangents which make an angle of 60º with each other at P.
5. Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
Steps of construction: i) Draw a line segment BC = 4.5 cm ii) With centres B and C, draw two arcs of radius 4.5 cm which intersect each other at A. iii) And join AC and AB. iv) Draw the perpendicular bisectors of AC and BC which intersect each other at O. v) With centre O, and radius OA or OB or OC draw a circle which will pass through A, B and C. Then, this is the required circumcircle of triangle ABC. On measuring the radius, we get OA = 2.6 cm6. Using ruler and compasses only.
(i) Construct triangle ABC, having given BC = 7 cm, AB-AC = 1 cm and ∠ABC = 45 o .
(ii) Inscribe a circle in the ΔABC constructed in (i) above.
Solution:
Steps of construction: i) Construction of triangle: a) Draw a line segment BC = 7 cm b) At B, draw a ray BX making an angle of 45 o and cut off BE = AB – AC = 1 cm c) Join EC and draw the perpendicular bisector of EC intersecting BX at A. d) Finally, join AC. Thus, ΔABC is the required triangle. ii) Construction of incircle: e) Draw the angle bisectors of ∠ABC and ∠ACB which intersect each other at O. f) From O, draw perpendicular OL to BC. g) With O as centre and OL as radius draw a circle which touches the sides of the ΔABC. This is the required in-circle of ΔABC. On measuring, we get the radius OL = 1.8 cm7. Using ruler and compasses only, draw an equilateral triangle of side 5 cm. Draw its inscribed circle. Measure the radius of the circle.
Solution:
Steps of Construction: i) Draw a line segment BC = 5 cm ii) With centres as B and C, draw two arcs of radius 5 cm each which intersect each other at A. iii) Then, join AB and AC. iv) Draw angle bisectors of ∠B and ∠C which intersect each other at O. v) Draw OL ⊥ BC, from O. vi) Now with centre O and radius OL, draw a circle which will touch the sides of ΔABC. On measuring the radius, we have OL = 1.4 cm.8. Using ruler and compasses only,
(i) Construct a triangle ABC with the following data:
Base AB = 6 cm, BC = 6.2 cm and ∠CAB = 60 o
(ii) In the same diagram, draw a circle which passes through the points A, B and C and mark its centre as O.
(iii) Draw a perpendicular from O to AB which meets AB in D.
(iv) Prove that AD = BD
Solution:
Steps of construction: i) Draw a line segment AB = 6 cm ii) Draw a ray at A, making an angle of 60 o with BC. iii) With B as centre and radius = 6.2 cm draw an arc which intersects AX ray at C. iv) Join BC. Then, ΔABC is the required triangle. v) Draw the perpendicular bisectors of AB and AC intersecting each other at O. vi) With centre O, and radius as OA or OB or OC, draw a circle which will pass through A, B and C. vii) From O, draw OD ⊥ AB. Proof: In right ΔOAD and ΔOBD OA = OB [Radii of same circle] OD = OD [Common] ∆OAD ≅ ∆OBD by RHS congruence criterion. Hence, by CPCT AD = BD9. Using ruler and compasses only construct a triangle ABC in which BC = 4 cm, ∠ACB = 45 o and perpendicular from A on BC is 2.5 cm. Draw a circle circumscribing the triangle ABC.
Solution:
Steps of Construction: i) Draw a line segment BC = 4 cm. ii) At C, draw a perpendicular line CX and from it, cut off CE = 2.5 cm. iii) Draw another perpendicular line EY from E. iv) From C, draw a ray making an angle of 45 o with CB, which intersects EY at A. v) Join AB. Then, ΔABC is the required triangle. vi) Draw perpendicular bisectors of sides AB and BC intersecting each other at O. vii) With centre O, and radius OB, draw a circle which will pass through A, B and C. On measuring, we have the radius OB = OC = OA = 2 cm.10. Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
(i) What do you call the point O?
(ii) What is the relation between the distances OA, OB and OC?
(iii) Does the perpendicular bisector of BC pass through O?
Solution:
i) O is called the circumcentre of circumcircle of ΔABC. ii) OA, OB and OC are the radii of the circumcircle. iii) Yes, the perpendicular bisector of BC will pass through O.11. The bisectors of angles A and B of a scalene triangle ABC meet at O.
i) What is the point O called?
ii) OR and OQ are drawn perpendiculars to AB and CA respectively. What is the relation between OR and OQ?
iii) What is the relation between angle ACO and angle BCO?
Solution:
i) O is called the incentre of the incircle of ΔABC. ii) OR and OQ are the radii of the incircle and OR = OQ. iii) OC is the bisector of angle C Thus, ∠ACO = ∠BCO12. i) Using ruler and compasses only, construct a triangle ABC in which AB = 8 cm, BC = 6 cm and CA = 5 cm.
ii) Find its incentre and mark it I.
iii) With I as centre, draw a circle which will cut off 2 cm chords from each side of the triangle.
Solution:
Steps of construction: i) Draw a line segment BC = 6 cm. ii) Draw an arc with centre B and radius 8 cm. iii) Draw another arc with centre C and radius 5 cm which intersects the first arc at A. iv) Join AB and AC. Thus, ΔABC is the required triangle. v) Draw the angle bisectors of ∠B and ∠A which intersect each other at I. Then I is the incentre of the triangle ABC. vi) Through I, draw ID ⊥ AB. vii) Now from D, cut off DP = DQ = 2/2 = 1 cm viii) With centre I, and radius IP or IQ, draw a circle which will intersect each side of triangle ABC cutting chords of 2 cm each.13. Construct an equilateral triangle ABC with side 6 cm. Draw a circle circumscribing the triangle ABC.
Solution:
Steps of construction: i) Draw a line segment BC = 6 cm ii) Draw two arcs of radius 6 cm with centres B and C, which intersect each other at A. iii) Then, join AC and AB. iv) Draw perpendicular bisectors of AC, AB and BC intersecting each other at O. v) Draw a circle with centre O, and radius OA or OB or OC which will pass through A, B and C. Then, this is the required circumcircle of triangle ABC.14. Construct a circle, inscribing an equilateral triangle with side 5.6 cm.
Solution:
Steps of Construction: i) Draw a line segment BC = 5.6 cm ii) With centres B and C, draw two arcs of 5.6 cm radius each which intersect each other at A. iii) And, join AB and AC. iv) Draw angle bisectors of ∠B and ∠C which intersect each other at O. v) From O, draw OL ⊥ BC. vi) Now with centre O and radius OL, draw a circle which will touch the sides of ΔABC . Thus, this is the required circle.Benefits of ICSE Class 10 Maths Selina Solutions Chapter 19
The ICSE Class 10 Maths Selina Solutions Chapter 19 on constructions offers several benefits to students:Development of Geometric Skills : By learning constructions, students develop practical skills in drawing accurate geometric figures using basic tools like a compass and ruler. This improves their spatial awareness and ability to visualize and manipulate geometric shapes.
Understanding Geometric Principles : Constructions reinforce fundamental geometric principles such as angle bisectors, perpendicular bisectors, and properties of triangles and quadrilaterals. This deepens students' understanding of geometry beyond theoretical concepts.
Problem-Solving Skills : Constructions require students to apply logical reasoning and problem-solving strategies to achieve specific geometric configurations. This enhances their analytical thinking and prepares them for more complex mathematical problems.
Preparation for Exams : Mastery of constructions is essential for scoring well in exams. Questions on geometric constructions often appear in both theoretical and practical formats, and thorough understanding ensures students can tackle them effectively.
Real-World Applications : Geometric constructions have practical applications in fields such as architecture, engineering, and design. Learning these skills early equips students with tools that can be useful in future academic and professional endeavors.
ICSE Class 10 Maths Selina Solutions Chapter 19 FAQs
Which is the hardest chapter of class 10 maths?
Which is the most important chapter in maths class 10 ICSE?
What happens if you fail maths in ICSE 10?
How to score 90+ in class 10?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
