Competitive Exams

IIT JEE, NEET, ESE, GATE, AE/JE, Olympiad

Only IAS

UPSC, State PSC

School Preparation

Foundation (Class 6-12), Commerce, Arts, CuriousJr (1st - 8th), Science, International Boards

Govt Exam

Judiciary, SSC, Defence, Teaching, JAIIB & CAIIB, BIHAR EXAMS WALLAH, UP Exams, Railway, Nursing Exams, Banking, WB Exams

UG & PG Entrance Exams

MBA, IPMAT, IIT JAM, LAW, CUET UG, UGC NET, GMAT, Design & Architecture, Pharma, CSIR NET, CUET PG, NEET PG

FINANCE

CA, CS, Finance Courses, ACCA

Others

English Wallah, Online Degrees

English Proficiency Test

IELTS, TOEFL

Agriculture

Linear Momentum Formula Explained with Solved Examples

The concept of kinetic energy is related to the conservation of mechanical energy, which states that the total mechanical energy (the sum of kinetic and potential energy) of an isolated system remains constant unless acted upon by external forces.

Murtaza Mushtaq11 Sept, 2023

Linear Momentum Formula is the energy an object possesses due to its motion. It's one of the fundamental concepts in physics and is defined as the energy that an object has because of its velocity (speed) and mass. In other words, when an object is in motion, it has kinetic energy associated with that motion.

The formula for kinetic energy i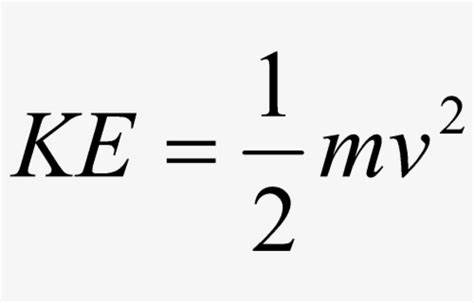s:

Where: - KE represents the kinetic energy in joules (J). - m is the mass of the object in kilograms (kg). - v is the velocity (speed) of the object in meters per second (m/s).

Key points about kinetic energy:

Depends on Mass and Velocity: Kinetic energy is directly proportional to both the mass and the square of the velocity of the object. This means that increasing either the mass or the velocity will increase the kinetic energy.
Scalar Quantity: Kinetic energy is a scalar quantity, meaning it only has magnitude (a numerical value) and no direction. It's always positive or zero and does not have a directional component.
Conservation of Energy: According to the law of conservation of energy, the total mechanical energy (which includes both kinetic and potential energy) of an isolated system remains constant if there are no external forces acting on it. This principle is often used in various physical problems.
Units: The SI unit of kinetic energy is the joule (J), which is equivalent to one kilogram-meter squared per second squared (1 kg·m^2/s^2).

Also Check - Kinetic Energy Formula

In practical terms, kinetic energy helps describe how fast an object is moving and how much "energy of motion" it possesses. For example, a speeding car has a significant amount of kinetic energy, and a slowly moving object has less kinetic energy. Understanding kinetic energy is essential in many areas of physics and engineering, particularly in the analysis of motion and collisions. Kinetic energy is a fundamental concept in physics that represents the energy an object possesses due to its motion. It's a measure of how much work an object could do because of its motion. In other words, it quantifies the energy associated with the movement of an object. Kinetic energy depends on two factors: - Mass (m): The mass of the object in kilograms (kg). This represents how much matter is in motion.

Also Check - Unit, Dimension & Vector Formula

- Velocity (v): The velocity of the object in meters per second (m/s). This represents how fast the objectis moving.

Linear Momentum (p):

Linear momentum, often denoted as "p," is another fundamental concept in physics that describes the quantity of motion of an object. It is a vector quantity, meaning it has both magnitude and direction. Linear momentum depends on two factors: - Mass (m): Just like in kinetic energy, it represents the mass of the object in kilograms (kg).

Also Check - Work, Energy & Power Formula

- Velocity (v): This represents the velocity of the object in meters per second (m/s). However, unlike kinetic energy, linear momentum doesn't involve squaring the velocity. The formula for linear momentum is:

p = m * v Linear momentum is directly proportional to both the mass and the velocity of the object. Now, let's define the relationship between kinetic energy and linear momentum: The relationship between kinetic energy (KE) and linear momentum (p) can be expressed as follows: KE = (1/2) * (p ² / m) This equation shows that kinetic energy is directly related to the square of the magnitude of linear momentum (p) and inversely related to the mass (m) of the object. In essence, it tells us that as an object's linear momentum increases (either by increasing its velocity or mass), its kinetic energy also increases, but the relationship is quadratic, meaning that a small increase in momentum can result in a much larger increase in kinetic energy.

Some Examples

Let's go through a couple of examples to illustrate the relationship between kinetic energy (KE), linear momentum (p), and how changes in mass or velocity affect them. Example 1: Car Moving on the Highway Imagine a car traveling on a highway with a mass of 1,000 kilograms (m) and a velocity of 30 meters per second (m/s).

Calculate the linear momentum (p):

p = m * v = 1,000 kg * 30 m/s = 30,000 kg m/s

Calculate the kinetic energy (KE):

KE = (1/2) * m * v^2 = (1/2) * 1,000 kg * (30 m/s)^2 = 450,000 J (joules) Now, let's see how changes in velocity affect kinetic energy and momentum: Example 2: Doubling the Velocity Let's say the car's velocity is doubled to 60 m/s while keeping the mass constant at 1,000 kg.

Calculate the new linear momentum (p):

p = m * v = 1,000 kg * 60 m/s = 60,000 kg m/s

Calculate the new kinetic energy (KE)

KE = (1/2) * m * v^2 = (1/2) * 1,000 kg * (60 m/s)^2 = 1,800,000 J By doubling the velocity while keeping the mass constant, the linear momentum doubled from 30,000 kg m/s to 60,000 kg m/s, but the kinetic energy increased fourfold from 450,000 J to 1,800,000 J. This demonstrates how kinetic energy is proportional to the square of velocity. Example 3: Doubling the Mass Now, let's keep the velocity at 30 m/s but double the mass of the car to 2,000 kg.

Calculate the new linear momentum (p):

p = m * v = 2,000 kg * 30 m/s = 60,000 kg m/s

Calculate the new kinetic energy (KE):

KE = (1/2) * m * v^2 = (1/2) * 2,000 kg * (30 m/s)^2 = 900,000 J By doubling the mass while keeping the velocity constant, the linear momentum doubled from 30,000 kg m/s to 60,000 kg m/s, but the kinetic energy only doubled from 450,000 J to 900,000 J. This shows that kinetic energy is directly proportional to mass but not linearly; it increases linearly with mass. These examples illustrate the relationship between kinetic energy and linear momentum and how changes in mass and velocity affect them. Kinetic energy is affected by both mass and the square of velocity, while linear momentum depends linearly on both mass and velocity.

Linear Momentum Formula FAQs

What is kinetic energy, and how is it different from linear momentum?

Kinetic Energy (KE): Kinetic energy is the energy an object possesses due to its motion. It depends on both the mass and the square of the velocity of the object. KE is a scalar quantity and is measured in joules (J).

How are kinetic energy and linear momentum related mathematically?

The mathematical relationship between kinetic energy (KE) and linear momentum (p) is given by the formula: KE = (1/2) * (p^2 / m). This equation shows that kinetic energy is proportional to the square of the magnitude of linear momentum and inversely proportional to the mass of the object.

What happens to kinetic energy when an object's velocity doubles?

When an object's velocity doubles, its kinetic energy increases by a factor of four. This is because kinetic energy is directly proportional to the square of velocity. So, if the velocity is doubled, the kinetic energy will be four times greater.

What physical principles are associated with kinetic energy and linear momentum?

Conservation of Energy: The concept of kinetic energy is related to the conservation of mechanical energy, which states that the total mechanical energy (the sum of kinetic and potential energy) of an isolated system remains constant unless acted upon by external forces. - Conservation of Linear Momentum: Linear momentum is associated with the conservation of linear momentum principle, which states that in the absence of external forces, the total linear momentum of an isolated system remains constant. This principle is often applied in the analysis of collisions and interactions between objects.

🔥 Trending Blogs

NCERT Solutions Federalism Class 10 Questions and Answers PDF

NCERT Solutions for Gravitation Class 9 Questions Answers PDF

NCERT Ram Lakshman Parshuram Samvad Question Answer for Class 10

NCERT Solutions Atmakatha Class 10 Question Answer Hindi Kshitij

CBSE Class 10 Compartment Result 2025 Anytime @results.cbse.nic.in, Diect Link Here

Talk to a counsellorHave doubts? Our support team will be happy to assist you!

7019243492

07019243492

Check out these Related Articles

SCHOOL PREPARATION

CBSE Compartment Result 2025 OUT, Direct Link to Download Here

Read Full Story

1 Aug 2025, 11:54 pm

CLASS 12 EXAM

CBSE Class 12 Compartment Result 2025 Out, Direct Link To Download Marksheet

Read Full Story

1 Aug 2025, 11:54 pm

ICSETEN

ICSE ISC Improvement Results 2025 Out @cisce.org Check 10th 12th Result

Read Full Story

1 Aug 2025, 05:51 pm

SCHOOL

NCERT Solutions Class 11 chemistry Chapter 2 Structure of atom

Read Full Story

1 Aug 2025, 05:49 pm

CLASS 6 EXAM

NCERT Class 6 Maths Ganita Prakash Chapter 9 Symmetry PDF

Read Full Story

31 Jul 2025, 01:36 pm

CLASS 7 EXAM

NCERT Solutions for Class 7 Maths Ganita Prakash Chapter 3 PDF

Read Full Story

30 Jul 2025, 12:49 pm

CLASS 7 EXAM

NCERT Solutions for Class 7 Science Curiosity Chapter 7

Read Full Story

30 Jul 2025, 05:07 pm

CLASS 7 EXAM

NCERT Solutions for Class 7 Science Curiosity (2025-26 Edition)

Read Full Story

25 Jul 2025, 02:18 pm

CLASS 7 EXAM

NCERT Solutions for Class 7 Science Curiosity Chapter 9 Life Processes in Animals

Read Full Story

11 Jul 2025, 07:00 pm

Join 15 Million students on the app today!

Live & recorded classes available at ease

Dashboard for progress tracking

Millions of practice questions at your fingertips

Free Learning Resources

PW Books

Notes (Class 10-12)

Class 10 Math's Notes

Class 10 Chemistry Notes

Class 10 Physics Notes

lass 10 Biology Notes

Aptitude & Reasoning

Class 10 Geography

Physics Class 11 Notes

Class 11 Chemistry Notes

Maths Notes Class 11

Zoology Class 11

Class 11 Botany Notes

Physics Class 12 notes

Chemistry Class 12

Maths Notes Class 12

Zoology class 12

Class 12th Botany Notes

PW Study Materials

Arjuna JEE Study Material

JEE 5 PYQs

JEE Mind Maps

Yakeen Study Material

NCERT Punch

Arjuna Neet Study Material

NEET PYQs

CBSE Sample Paper

CBSE Question Bank

Udaan For Class 10th Study Material

Notes (Class 6-9)

Class-6 Theory & Notes

Math's Notes for class 7

Science Notes for class 7

Class 8 Math Notes

Class 8 Chemistry Notes

Class 8 Physics Notes

Class 8 Biology Notes

Class 8 SST Notes

Class 9 Math's Notes

Class 9 Physics Notes

Class 9 Chemistry Notes

Class 9 Biology Notes

Ncert Solutions

NCERT Solutions For Class 6

NCERT Solutions For class 7

NCERT Solutions for class 8

NCERT Solutions for class 9

NCERT Solutions for class 10

NCERT Solutions for class 11

NCERT Solutions for Class 12

NCERT Solutions For Class 6

Govt Exams

Entrance Exams

Our Other Websites

Class 6th to 12th Online Courses

Class 12 Online Course

Class 11 Online Course

Class 10 Online Course

Class 9 Online Course

Class 8 Online Course

Govt Job Exams Courses

SSC Online Coaching

Bank Exam Online Coaching

TET Online Coaching

JAIIB & CAIIB Online Coaching

Bihar Exam Online Coaching

UPSC Coaching

UPSC Online Coaching

UPSC Offline & Hybrid Coaching

State PSC Online Coaching

UPPSC Online Coaching

BPSC Online Coaching

Defence Exam Coaching

NDA Online Coaching

CDS Online Coaching

AFCAT Online Coaching

Agniveer Online Coaching

Gate Exam Coaching

Civil Engineering Courses

Mechanical Engineering Courses

Formulas

Other Exams

Company Secretary Exam

Know about Physics Wallah

Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.

We Stand Out because

We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.

Our Key Focus Areas

Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.

What Makes Us Different

Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others

The formula for kinetic energy is:

Where: - KE represents the kinetic energy in joules (J). - m is the mass of the object in kilograms (kg). - v is the velocity (speed) of the object in meters per second (m/s).

Key points about kinetic energy:

Depends on Mass and Velocity: Kinetic energy is directly proportional to both the mass and the square of the velocity of the object. This means that increasing either the mass or the velocity will increase the kinetic energy.
Scalar Quantity: Kinetic energy is a scalar quantity, meaning it only has magnitude (a numerical value) and no direction. It's always positive or zero and does not have a directional component.
Conservation of Energy: According to the law of conservation of energy, the total mechanical energy (which includes both kinetic and potential energy) of an isolated system remains constant if there are no external forces acting on it. This principle is often used in various physical problems.
Units: The SI unit of kinetic energy is the joule (J), which is equivalent to one kilogram-meter squared per second squared (1 kg·m^2/s^2).

Also Check - Kinetic Energy Formula

Also Check - Unit, Dimension & Vector Formula

- Velocity (v): The velocity of the object in meters per second (m/s). This represents how fast the objectis moving.

Linear Momentum (p):

Also Check - Work, Energy & Power Formula

Some Examples

Calculate the linear momentum (p):

p = m * v = 1,000 kg * 30 m/s = 30,000 kg m/s

Calculate the kinetic energy (KE):

Calculate the new linear momentum (p):

p = m * v = 1,000 kg * 60 m/s = 60,000 kg m/s

Calculate the new kinetic energy (KE)

Calculate the new linear momentum (p):

p = m * v = 2,000 kg * 30 m/s = 60,000 kg m/s

Calculate the new kinetic energy (KE):