NCERT Solutions for Class 8 Maths Chapter 12 Factorisation
Neha Tanna27 Jun, 2024
Share
NCERT Solutions for Class 8 Maths Chapter 12: The purpose of the NCERT Solutions for Class 8 Maths Chapter 12 is to assist students in grasping the material and gaining thorough understanding of the different kinds of questions that are asked in the CBSE Class 8 Mathematics Examinations.
There are suitable answers for every question, which would help update the CBSE Class 8 Mathematics syllabus. According to the CBSE syllabus, extremely qualified subject matter specialists created the NCERT Solutions for Class 8 Maths Chapter 12. Students can simplify their final-minute review by using the Class 8 Maths NCERT Solutions. Students who wish to study offline can download the PDF.NCERT Solutions for Class 8 Maths Chapter 12 Overview
The purpose of NCERT Solutions is to aid students in learning the subject matter and developing a thorough comprehension of the various question types seen in the CBSE Factorization Class 8 Mathematics Examinations. Every question has an appropriate response, which will be useful for revising the CBSE Class 8 Mathematics syllabus. The Maths Class 8 solutions are created by highly certified subject matter specialists, as per the CBSE guideline. Students can use the Class 8 Maths NCERT Solutions to make their last-minute review easier. Students can download the PDF if they would like to study offline.NCERT Solutions for Class 8 Maths Chapter 12 PDF
Here we have provided NCERT Solutions for Class 8 Maths Chapter 12 for the ease of students so that they can just download the pdf and use it easily without the internet. These NCERT Solutions for Class 8 Maths Chapter 12 will help students understand the chapter better.NCERT Solutions for Class 8 Maths Chapter 12 PDF
NCERT Solutions for Class 8 Maths Chapter 12
Here we have provided NCERT Solutions for Class 8 Maths Chapter 12 for the ease of students so that they can prepare better for their upcoming exams -1. Find the common factors of the given terms.
(i) 12x, 36
(ii) 2y, 22xy
(iii) 14 pq, 28p 2 q 2
(iv) 2x, 3x 2 , 4
(v) 6 abc, 24ab 2 , 12a 2 b
(vi) 16 x 3 , – 4x 2 , 32 x
(vii) 10 pq, 20qr, 30 rp
(viii) 3x 2 y 3 , 10x 3 y 2 , 6x 2 y 2 z
Solution:
(i) Factors of 12x and 36 12x = 2×2×3×x 36 = 2×2×3×3 Common factors of 12x and 36 are 2, 2, 3 and , 2×2×3 = 12 (ii) Factors of 2y and 22xy 2y = 2×y 22xy = 2×11×x×y Common factors of 2y and 22xy are 2, y and ,2×y = 2y (iii) Factors of 14pq and 28p 2 q 2 14pq = 2x7xpxq 28p 2 q 2 = 2x2x7xpxpxqxq Common factors of 14 pq and 28 p 2 q 2 are 2, 7 , p , q and, 2x7xpxq = 14pq (iv) Factors of 2x, 3x 2 and 4 2x = 2×x 3x 2 = 3×x×x 4 = 2×2 Common factors of 2x, 3x 2 and 4 is 1. (v) Factors of 6abc, 24ab 2 and 12a 2 b 6abc = 2×3×a×b×c 24ab 2 = 2×2×2×3×a×b×b 12 a 2 b = 2×2×3×a×a×b Common factors of 6 abc, 24ab 2 and 12a 2 b are 2, 3, a, b and, 2×3×a×b = 6ab (vi) Factors of 16x 3 , -4x 2 and 32x 16 x 3 = 2×2×2×2×x×x×x – 4x 2 = -1×2×2×x×x 32x = 2×2×2×2×2×x Common factors of 16 x 3 , – 4x 2 and 32x are 2,2, x and, 2×2×x = 4x (vii) Factors of 10 pq, 20qr and 30rp 10 pq = 2×5×p×q 20qr = 2×2×5×q×r 30rp= 2×3×5×r×p Common factors of 10 pq, 20qr and 30rp are 2, 5 and, 2×5 = 10 (viii) Factors of 3x 2 y 3 , 10x 3 y 2 and 6x 2 y 2 z 3x 2 y 3 = 3×x×x×y×y×y 10x 3 y 2 = 2×5×x×x×x×y×y 6x 2 y 2 z = 3×2×x×x×y×y×z Common factors of 3x 2 y 3 , 10x 3 y 2 and 6x 2 y 2 z are x 2 , y 2 and, x 2 ×y 2 = x 2 y 22.Factorise the following expressions.
(i) 7x–42
(ii) 6p–12q
(iii) 7a 2 + 14a
(iv) -16z+20 z 3
(v) 20l 2 m+30alm
(vi) 5x 2 y-15xy 2
(vii) 10a 2 -15b 2 +20c 2
(viii) -4a 2 +4ab–4 ca
(ix) x 2 yz+xy 2 z +xyz 2
(x) ax 2 y+bxy 2 +cxyz
Solution:
(vii) 10a
2
-15b
2
+20c
2
10a
2
= 2×5×a×a
– 15b
2
= -1×3×5×b×b
20c
2
= 2×2×5×c×c
Common factor of 10 a
2
, 15b
2
and 20c
2
is 5
10a
2
-15b
2
+20c
2
= 5(2a
2
-3b
2
+4c
2
)
(viii) – 4a
2
+4ab-4ca
– 4a
2
= -1×2×2×a×a
4ab = 2×2×a×b
– 4ca = -1×2×2×c×a
Common factor of – 4a
2
, 4ab , – 4ca are 2, 2, a i.e. 4a
So,
– 4a
2
+4 ab-4 ca = 4a(-a+b-c)
(ix) x
2
yz+xy
2
z+xyz
2
x
2
yz = x×x×y×z
xy
2
z = x×y×y×z
xyz
2
= x×y×z×z
Common factor of x
2
yz , xy
2
z and xyz
2
are x, y, z i.e. xyz
Now, x
2
yz+xy
2
z+xyz
2
= xyz(x+y+z)
(x) ax
2
y+bxy
2
+cxyz
ax
2
y = a×x×x×y
bxy
2
= b×x×y×y
cxyz = c×x×y×z
Common factors of a x
2
y ,bxy
2
and cxyz are xy
Now, ax
2
y+bxy
2
+cxyz = xy(ax+by+cz)
3. Factorise.
(i) x 2 +xy+8x+8y
(ii) 15xy–6x+5y–2
(iii) ax+bx–ay–by
(iv) 15pq+15+9q+25p
(v) z–7+7xy–xyz
Solution :
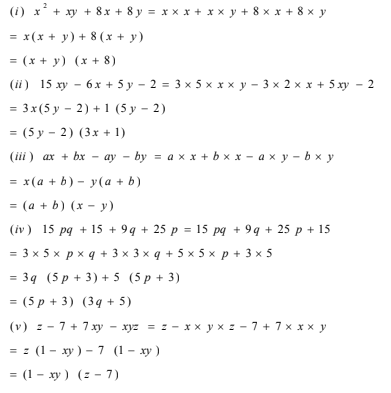
NCERT Solutions for Class 8 Maths Chapter 12 Ex 12.2
1. Factorise the following expressions.
(i) a 2 +8a+16
(ii) p 2 –10p+25
(iii) 25m 2 +30m+9
(iv) 49y 2 +84yz+36z 2
(v) 4x 2 –8x+4
(vi) 121b 2 –88bc+16c 2
(vii) (l+m) 2 –4lm (Hint: Expand (l+m) 2 first)
(viii) a 4 +2a 2 b 2 +b 4
Solution:
(i) a 2 +8a+16 = a 2 +2×4×a+4 2 = (a+4) 2 Using the identity (x+y) 2 = x 2 +2xy+y 2 (ii) p 2 –10p+25 = p 2 -2×5×p+5 2 = (p-5) 2 Using the identity (x-y) 2 = x 2 -2xy+y 2 (iii) 25m 2 +30m+9 = (5m) 2 +2×5m×3+3 2 = (5m+3) 2 Using the identity (x+y) 2 = x 2 +2xy+y 2 (iv) 49y 2 +84yz+36z 2 =(7y) 2 +2×7y×6z+(6z) 2 = (7y+6z) 2 Using the identity (x+y) 2 = x 2 +2xy+y 2 (v) 4x 2 –8x+4 = (2x) 2 -2×4x+2 2 = (2x-2) 2 Using the identity (x-y) 2 = x 2 -2xy+y 2 (vi) 121b 2 -88bc+16c 2 = (11b) 2 -2×11b×4c+(4c) 2 = (11b-4c) 2 Using the identity (x-y) 2 = x 2 -2xy+y 2 (vii) (l+m) 2 -4lm (Hint: Expand (l+m) 2 first) Expand (l+m) 2 using the identity (x+y) 2 = x 2 +2xy+y 2 (l+m) 2 -4lm = l 2 +m 2 +2lm-4lm = l 2 +m 2 -2lm = (l-m) 2 Using the identity (x-y) 2 = x 2 -2xy+y 2 (viii) a 4 +2a 2 b 2 +b 4 = (a 2 ) 2 +2×a 2× b 2 +(b 2 ) 2 = (a 2 +b 2 ) 2 Using the identity (x+y) 2 = x 2 +2xy+y 22. Factorise.
(i) 4p 2 –9q 2
(ii) 63a 2 –112b 2
(iii) 49x 2 –36
(iv) 16x 5 –144x 3 differ
(v) (l+m) 2 -(l-m) 2
(vi) 9x 2 y 2 –16
(vii) (x 2 –2xy+y 2 )–z 2
(viii) 25a 2 –4b 2 +28bc–49c 2
Solution:
(i) 4p 2 –9q 2 = (2p) 2 -(3q) 2 = (2p-3q)(2p+3q) Using the identity x 2 -y 2 = (x+y)(x-y) (ii) 63a 2 –112b 2 = 7(9a 2 –16b 2 ) = 7((3a) 2 –(4b) 2 ) = 7(3a+4b)(3a-4b) Using the identity x 2 -y 2 = (x+y)(x-y) (iii) 49x 2 –36 = (7x) 2 -6 2 = (7x+6)(7x–6) Using the identity x 2 -y 2 = (x+y)(x-y) (iv) 16x 5 –144x 3 = 16x 3 (x 2 –9) = 16x 3 (x 2 –9) = 16x 3 (x–3)(x+3) Using the identity x 2 -y 2 = (x+y)(x-y) (v) (l+m) 2 -(l-m) 2 = {(l+m)-(l–m)}{(l +m)+(l–m)} Using the identity x 2 -y 2 = (x+y)(x-y) = (l+m–l+m)(l+m+l–m) = (2m)(2l) = 4 ml (vi) 9x 2 y 2 –16 = (3xy) 2 -4 2 = (3xy–4)(3xy+4) Using the identity x 2 -y 2 = (x+y)(x-y) (vii) (x 2 –2xy+y 2 )–z 2 = (x–y) 2 –z 2 Using the identity (x-y) 2 = x 2 -2xy+y 2 = {(x–y)–z}{(x–y)+z} = (x–y–z)(x–y+z) Using the identity x 2 -y 2 = (x+y)(x-y) (viii) 25a 2 –4b 2 +28bc–49c 2 = 25a 2 –(4b 2 -28bc+49c 2 ) = (5a) 2 -{(2b) 2 -2(2b)(7c)+(7c) 2 } = (5a) 2 -(2b-7c) 2 Using the identity x 2 -y 2 = (x+y)(x-y) , we have = (5a+2b-7c)(5a-2b+7c)3. Factorise the expressions.
(i) ax 2 +bx
(ii) 7p 2 +21q 2
(iii) 2x 3 +2xy 2 +2xz 2
(iv) am 2 +bm 2 +bn 2 +an 2
(v) (lm+l)+m+1
(vi) y(y+z)+9(y+z)
(vii) 5y 2 –20y–8z+2yz
(viii) 10ab+4a+5b+2
(ix)6xy–4y+6–9x
Solution:
(i) ax 2 +bx = x(ax+b) (ii) 7p 2 +21q 2 = 7(p 2 +3q 2 ) (iii) 2x 3 +2xy 2 +2xz 2 = 2x(x 2 +y 2 +z 2 ) (iv) am 2 +bm 2 +bn 2 +an 2 = m 2 (a+b)+n 2 (a+b) = (a+b)(m 2 +n 2 ) (v) (lm+l)+m+1 = lm+m+l+1 = m(l+1)+(l+1) = (m+1)(l+1) (vi) y(y+z)+9(y+z) = (y+9)(y+z) (vii) 5y 2 –20y–8z+2yz = 5y(y–4)+2z(y–4) = (y–4)(5y+2z) (viii) 10ab+4a+5b+2 = 5b(2a+1)+2(2a+1) = (2a+1)(5b+2) (ix) 6xy–4y+6–9x = 6xy–9x–4y+6 = 3x(2y–3)–2(2y–3) = (2y–3)(3x–2)4.Factorise.
(i) a 4 –b 4
(ii) p 4 –81
(iii) x 4 –(y+z) 4
(iv) x 4 –(x–z) 4
(v) a 4 –2a 2 b 2 +b 4
Solution:
(i) a 4 –b 4 = (a 2 ) 2 -(b 2 ) 2 = (a 2 -b 2 ) (a 2 +b 2 ) = (a – b)(a + b)(a 2 +b 2 ) (ii) p 4 –81 = (p 2 ) 2 -(9) 2 = (p 2 -9)(p 2 +9) = (p 2 -3 2 )(p 2 +9) =(p-3)(p+3)(p 2 +9) (iii) x 4 –(y+z) 4 = (x 2 ) 2 -[(y+z) 2 ] 2 = {x 2 -(y+z) 2 }{ x 2 +(y+z) 2 } = {(x –(y+z)(x+(y+z)}{x 2 +(y+z) 2 } = (x–y–z)(x+y+z) {x 2 +(y+z) 2 } (iv) x 4 –(x–z) 4 = (x 2 ) 2 -{(x-z) 2 } 2 = {x 2 -(x-z) 2 }{x 2 +(x-z) 2 } = { x-(x-z)}{x+(x-z)} {x 2 +(x-z) 2 } = z(2x-z)( x 2 +x 2 -2xz+z 2 ) = z(2x-z)( 2x 2 -2xz+z 2 ) (v) a 4 –2a 2 b 2 +b 4 = (a 2 ) 2 -2a 2 b 2 +(b 2 ) 2 = (a 2 -b 2 ) 2 = ((a–b)(a+b)) 2 = (a – b) 2 (a + b) 25. Factorise the following expressions.
(i) p 2 +6p+8
(ii) q 2 –10q+21
(iii) p 2 +6p–16
Solution:
(i) p 2 +6p+8 We observed that 8 = 4×2 and 4+2 = 6 p 2 +6p+8 can be written as p 2 +2p+4p+8 Taking Common terms, we get p 2 +6p+8 = p 2 +2p+4p+8 = p(p+2)+4(p+2) Again, p+2 is common in both the terms. = (p+2)(p+4) This implies that p 2 +6p+8 = (p+2)(p+4) (ii) q 2 –10q+21 We observed that 21 = -7×-3 and -7+(-3) = -10 q 2 –10q+21 = q 2 –3q-7q+21 = q(q–3)–7(q–3) = (q–7)(q–3) This implies that q 2 –10q+21 = (q–7)(q–3) (iii) p 2 +6p–16 We observed that -16 = -2×8 and 8+(-2) = 6 p 2 +6p–16 = p 2 –2p+8p–16 = p(p–2)+8(p–2) = (p+8)(p–2) So, p 2 +6p–16 = (p+8)(p–2)NCERT Solutions for Class 8 Maths Chapter 12 Ex 12.3
1. Carry out the following divisions.
(i) 28x 4 ÷ 56x
(ii) –36y 3 ÷ 9y 2
(iii) 66pq 2 r 3 ÷ 11qr 2
(iv) 34x 3 y 3 z 3 ÷ 51xy 2 z 3
(v) 12a 8 b 8 ÷ (– 6a 6 b 4 )
Solution:
(i)28x 4 = 2×2×7×x×x×x×x 56x = 2×2×2×7×x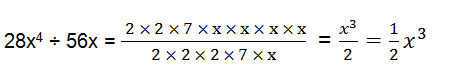
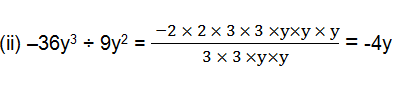
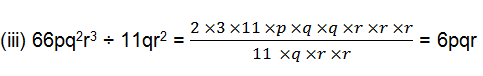
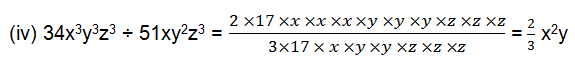
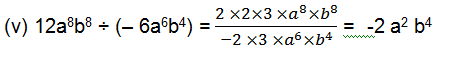
2. Divide the given polynomial by the given monomial.
(i)(5x 2 –6x) ÷ 3x
(ii)(3y 8 –4y 6 +5y 4 ) ÷ y 4
(iii) 8(x 3 y 2 z 2 +x 2 y 3 z 2 +x 2 y 2 z 3 )÷ 4x 2 y 2 z 2
(iv)(x 3 +2x 2 +3x) ÷2x
(v) (p 3 q 6 –p 6 q 3 ) ÷ p 3 q 3
Solution:
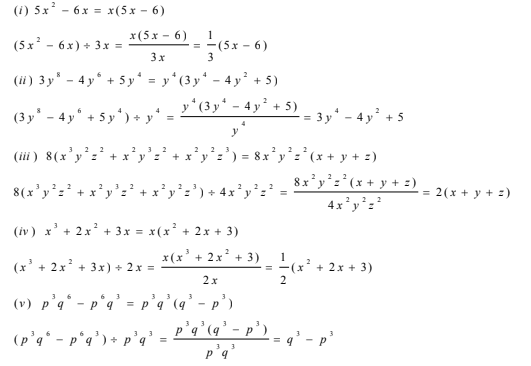
3. Work out the following divisions.
(i) (10x–25) ÷ 5
(ii) (10x–25) ÷ (2x–5)
(iii) 10y(6y+21) ÷ 5(2y+7)
(iv) 9x 2 y 2 (3z–24) ÷ 27xy(z–8)
(v) 96abc(3a–12)(5b–30) ÷ 144(a–4)(b–6)
Solution:
(i) (10x–25) ÷ 5 = 5(2x-5)/5 = 2x-5 (ii) (10x–25) ÷ (2x–5) = 5(2x-5)/( 2x-5) = 5 (iii) 10y(6y+21) ÷ 5(2y+7) = 10y×3(2y+7)/5(2y+7) = 6y (iv) 9x 2 y 2 (3z–24) ÷ 27xy(z–8) = 9x 2 y 2 ×3(z-8)/27xy(z-8) = xy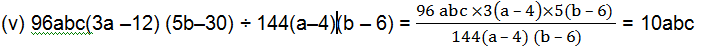
4. Divide as directed.
(i) 5(2x+1)(3x+5)÷ (2x+1)
(ii) 26xy(x+5)(y–4)÷13x(y–4)
(iii) 52pqr(p+q)(q+r)(r+p) ÷ 104pq(q+r)(r+p)
(iv) 20(y+4) (y 2 +5y+3) ÷ 5(y+4)
(v) x(x+1) (x+2)(x+3) ÷ x(x+1)
Solution:
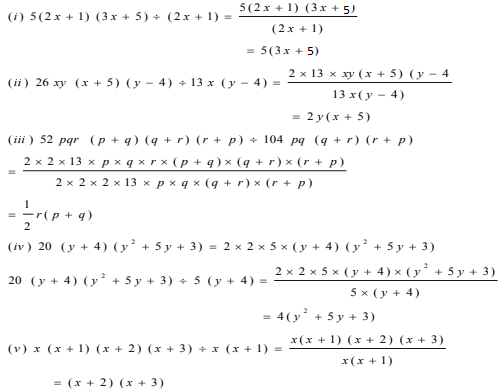
5. Factorise the expressions and divide them as directed.
(i) (y 2 +7y+10)÷(y+5)
(ii) (m 2 –14m–32)÷(m+2)
(iii) (5p 2 –25p+20)÷(p–1)
(iv) 4yz(z 2 +6z–16)÷2y(z+8)
(v) 5pq(p 2 –q 2 )÷2p(p+q)
(vi) 12xy(9x 2 –16y 2 )÷4xy(3x+4y)
(vii) 39y 3 (50y 2 –98) ÷ 26y 2 (5y+7)
Solution:
(i) (y 2 +7y+10)÷(y+5)
First, solve the equation (y 2 +7y+10) (y 2 +7y+10) = y 2 +2y+5y+10 = y(y+2)+5(y+2) = (y+2)(y+5) Now, (y 2 +7y+10)÷(y+5) = (y+2)(y+5)/(y+5) = y+2(ii) (m 2 –14m–32)÷ (m+2)
Solve for m 2 –14m–32, we have m 2 –14m–32 = m 2 +2m-16m–32 = m(m+2)–16(m+2) = (m–16)(m+2) Now, (m 2 –14m–32)÷(m+2) = (m–16)(m+2)/(m+2) = m-16(iii) (5p 2 –25p+20)÷(p–1)
Step 1: Take 5 common from the equation, 5p 2 –25p+20, we get 5p 2 –25p+20 = 5(p 2 –5p+4) Step 2: Factorise p 2 –5p+4 p 2 –5p+4 = p 2 –p-4p+4 = (p–1)(p–4) Step 3: Solve original equation (5p 2 –25p+20)÷(p–1) = 5(p–1)(p–4)/(p-1) = 5(p–4)(iv) 4yz(z 2 + 6z–16)÷ 2y(z+8)
Factorising z 2 +6z–16, z 2 +6z–16 = z 2 -2z+8z–16 = (z–2)(z+8) Now, 4yz(z 2 +6z–16) ÷ 2y(z+8) = 4yz(z–2)(z+8)/2y(z+8) = 2z(z-2)(v) 5pq(p 2 –q 2 ) ÷ 2p(p+q)
p 2 –q 2 can be written as (p–q)(p+q) using the identity. 5pq(p 2 –q 2 ) ÷ 2p(p+q) = 5pq(p–q)(p+q)/2p(p+q) = 5q(p–q)/2(vi) 12xy(9x 2 –16y 2 ) ÷ 4xy(3x+4y)
Factorising 9x 2 –16y 2 , we have 9x 2 –16y 2 = (3x) 2 –(4y) 2 = (3x+4y)(3x-4y) using the identity p 2 –q 2 = (p–q)(p+q) Now, 12xy(9x 2 –16y 2 ) ÷ 4xy(3x+4y) = 12xy(3x+4y)(3x-4y) /4xy(3x+4y) = 3(3x-4y)(vii) 39y 3 (50y 2 –98) ÷ 26y 2 (5y+7)
st solve for 50y 2 –98, we have 50y 2 –98 = 2(25y 2 –49) = 2((5y) 2 –7 2 ) = 2(5y–7)(5y+7) Now, 39y 3 (50y 2 –98) ÷ 26y 2 (5y+7) =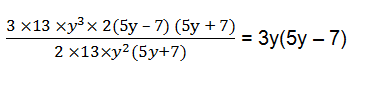
Benefits of NCERT Solutions for Class 8 Maths Chapter 12
NCERT Solutions for Class 8 Maths Chapter 12 on factorization offer several benefits to students:Structured Learning : NCERT Solutions provide a structured approach to learning the concepts of factorization. They break down complex problems into step-by-step solutions, making it easier for students to understand the underlying principles.
Clarity of Concepts : By following NCERT Solutions, students can achieve clarity in their understanding of factorization concepts such as finding the factors of a number, factorization of algebraic expressions, and methods like factorization by grouping.
Practice Questions : NCERT Solutions typically include a variety of practice questions with detailed solutions. These questions help students reinforce their learning and develop problem-solving skills by applying factorization techniques in different scenarios.
Exam Preparation : Since NCERT textbooks are commonly used for school exams, mastering NCERT Solutions ensures that students are well-prepared for their Class 8 exams. The solutions align closely with the curriculum prescribed by educational boards, ensuring comprehensive preparation.
Self-assessment : Students can use NCERT Solutions for self-assessment and gauge their understanding of the chapter. By attempting the exercises and comparing their answers with the provided solutions, students can identify areas where they need to focus more.
Accessible and Reliable : NCERT Solutions are easily accessible online and in print form, making them a reliable resource for both students and teachers. They are formulated by experts in the subject matter, ensuring accuracy and reliability.
Encourages Analytical Thinking : The process of solving problems using NCERT Solutions encourages students to think analytically and critically. They learn to identify patterns, apply different methods of factorization, and choose the most efficient approach to solve problems.
NCERT Solutions for Class 8 Maths Chapter 12 FAQs
Which is the hardest chapter in class 8 maths?
Which is the most easiest chapter in class 8 maths?
What is factorisation class 8 important points?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
