NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.4 Real Numbers
Ananya Gupta3 Jan, 2025
Share
NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.4: Exercise 1.4 of Chapter 1 Real Numbers focuses on the application of the Fundamental Theorem of Arithmetic which states that every composite number can be uniquely expressed as a product of prime numbers.
By solving these questions students develop a deeper understanding of how numbers can be decomposed into their prime factors which is important for further topics like HCF, LCM, and number theory. The NCERT Solutions for Exercise 1.4 provide step-by-step solutions, helping students learn the process of prime factorization and enhancing their problem-solving skills.NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.4 Overview
Exercise 1.4 of Chapter 1 Real Numbers focuses on the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 is either a prime number or can be uniquely factored into prime numbers. This exercise helps students practice prime factorization and its applications in solving problems related to real numbers. The problems require finding the prime factorization of numbers and using these factors to simplify expressions or solve number-theoretic problems. The exercise emphasizes the importance of prime factorization in understanding the structure of numbers and forms the basis for further study in number theory, such as finding the Highest Common Factor (HCF) and Least Common Multiple (LCM). The solutions provide clear, step-by-step explanations to help students master these concepts and apply them in various mathematical scenarios.NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.4 PDF
The NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.4 provide clear and detailed explanations on the Fundamental Theorem of Arithmetic and its applications. These solutions help in understanding how to find the prime factorization of numbers and apply this concept to solve various number-theoretic problems. To access the PDF of the solutions, click on the link below.NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.4 PDF
NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.4
Here are the NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.4. By solving these problems, students strengthen their understanding of prime numbers and their importance in number theory which is essential for topics such as HCF, LCM, and simplifying fractions. The solutions provide clear, step-by-step explanations to help students master the concept of prime factorization and its applications.1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion.
(i) 13/3125 (ii) 17/8 (iii) 64/455 (iv) 15/1600 (v) 29/343 (vi) 23/(2 3 5 2 ) (vii) 129/(2 2 5 7 7 5 ) (viii) 6/15 (ix) 35/50 (x) 77/210
Solutions:
Note: If the denominator has only factors of 2 and 5 or in the form of 2 m ×5 n, then it has a terminating decimal expansion.
If the denominator has factors other than 2 and 5, then it has a non-terminating decimal expansion.(i) 13/3125
Factorising the denominator, we get 3125 = 5 × 5 × 5 = 5 5 Since the denominator has only 5 as its factor, 13/3125 has a terminating decimal expansion.(ii) 17/8
Factorising the denominator, we get8 = 2×2×2 = 2 3
Since the denominator has only 2 as its factor, 17/8 has a terminating decimal expansion.(iii) 64/455
Factorising the denominator, we get 455 = 5×7×13 Since the denominator is not in the form of 2 m × 5 n , 64/455 has a non-terminating decimal expansion.(iv) 15/ 1600
Factorising the denominator, we get 1600 = 2 6 ×5 2 Since the denominator is in the form of 2 m × 5 n , 15/1600 has a terminating decimal expansion.(v) 29/343
Factorising the denominator, we get 343 = 7×7×7 = 7 3 Since the denominator is not in the form of 2 m × 5 n , 29/343 has a non-terminating decimal expansion.(vi)23/(2 3 5 2 )
Clearly, the denominator is in the form of 2 m × 5 n . Hence, 23/ (2 3 5 2 ) has a terminating decimal expansion.(vii) 129/(2 2 5 7 7 5 )
As you can see, the denominator is not in the form of 2 m × 5 n . Hence, 129/ (2 2 5 7 7 5 ) has a non-terminating decimal expansion.(viii) 6/15
6/15 = 2/5 Since the denominator has only 5 as its factor, 6/15 has a terminating decimal expansion.(ix) 35/50
35/50 = 7/10 Factorising the denominator, we get 10 = 2 × 5 Since the denominator is in the form of 2 m × 5 n , 35/50 has a terminating decimal expansion.(x) 77/210
77/210 = (7× 11)/ (30 × 7) = 11/30 Factorising the denominator, we get 30 = 2 × 3 × 5 As you can see, the denominator is not in the form of 2 m × 5 n . Hence, 77/210 has a non-terminating decimal expansion.2. Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.
Solutions:
(i) 13/3125
13/3125 = 0.00416
(ii) 17/8
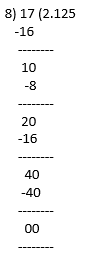17/8 = 2.125
(iii) 64/455 has a non-terminating decimal expansion.
(iv)15/ 1600
15/1600 = 0.009375
(v) 29/ 343 has a non-terminating decimal expansion.
(vi)23/ (2 3 5 2 ) = 23/(8×25)= 23/200
23/ (2
3
5
2
) = 0.115
(vii) 129/ (2 2 5 7 7 5 ) has a non-terminating decimal expansion.
(viii) 6/15 = 2/5
(ix) 35/50 = 7/10
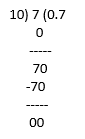35/50 = 0.7
(x) 77/210 has a non-terminating decimal expansion.
3. The following real numbers have decimal expansions, as given below. In each case, decide whether they are rational or not. If they are rational and of the form, p q, what can you say about the prime factors of q?
(i) 43.123456789
(ii) 0.120120012000120000. . .
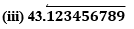
Solutions:
(i) 43.123456789 Since it has a terminating decimal expansion, it is a rational number in the form of p/q, and q has factors of 2 and 5 only. (ii) 0.120120012000120000. . . Since it has a non-terminating and non-repeating decimal expansion, it is an irrational number.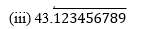
Since it has a non-terminating but repeating decimal expansion, it is a rational number in the form of p/q, and q has factors other than 2 and 5.
Benefits of Solving NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.4
- Understanding Prime Factorization : Exercise 1.4 focuses on prime factorization, which is an essential concept in number theory. Solving these problems helps students understand how every composite number can be broken down into a unique product of prime numbers, fostering a deeper grasp of number properties.
- Foundation for Advanced Topics : Prime factorization plays a crucial role in finding the Highest Common Factor (HCF) and Least Common Multiple (LCM), which are fundamental concepts used in various mathematical applications and higher studies.
- Strengthens Problem-Solving Skills : By practicing prime factorization and applying it to different problems, students enhance their logical thinking, accuracy, and ability to break down complex problems into simpler steps.
- Improves Understanding of Real Numbers : This exercise helps solidify the understanding of real numbers, especially in the context of divisibility, which is essential for further study in algebra and number theory.
- Exam Preparation : The problems in this exercise are designed to be exam-friendly, helping students practice for board exams. Regular practice boosts speed, accuracy, and confidence during exams.
- Boosts Analytical Thinking : The process of prime factorization and recognizing patterns in numbers helps students develop their analytical thinking skills, which are useful not only in mathematics but also in problem-solving situations in everyday life.
- Clear and Structured Learning : The NCERT solutions provide step-by-step guidance, making the learning process systematic and easy to follow. Students can gradually build their understanding, ensuring a strong conceptual foundation.
NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.4 FAQs
Are integers real numbers?
Can a real number be negative?
Are fractions real numbers?
Are whole numbers real numbers?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
