NCERT Solutions for Class 8 Maths Chapter 9 Mensuration
Neha Tanna26 Jun, 2024
Share
NCERT Solutions for Class 8 Maths Chapter 9: NCERT Solutions for Class 8 Maths Chapter 9 A crucial tool for CBSE students is measurement. It gives students a good understanding of the chapter and, more particularly, the kinds of questions that might be posted on the test and how to respond to them. To assist students in preparing for exams and clearing up any confusion, we offer all of the exercise-by-exercise NCERT Class 8 Math Solutions.
Mensuration is the domain of mathematics that studies geometric forms and their properties, such as length, volume, shape, surface area, lateral surface area, etc. These NCERT Solutions for Class 8 Maths provide comprehensive explanations of all the key mensuration formulas and characteristics of various geometric forms and figures, along with answers to questions about mensuration topics. The subject matter experts here solve challenges about the area and perimeter of various planar closed figures, such as quadrilaterals.NCERT Solutions for Class 8 Maths Chapter 9 Overview
Students studied the area and perimeter of closed plane forms, such as squares, rectangles, triangles, and circles, in the previous grade. Students will study the surface area and volume of solids (cube, cuboid, and cylinder), the area of a trapezium, the area of quadrilateral, the area of special quadrilaterals, the area of a polygon, solid forms, volume, and capacity in Class 8 CBSE Maths Chapter 9. For help with the exercise problems, students can refer to the NCERT Solutions for Class 8 in this chapter.NCERT Solutions for Class 8 Maths Chapter 9 PDF
Since mensuration is a topic with practical applications, try working through the Class 8 Maths Chapter 9 questions with answers from NCERT. Experts in the field have created all of the NCERT solutions, which align with the most recent CBSE syllabus to ensure that students achieve top grades. Here we have also provided NCERT Solutions for Class 8 Maths Chapter 9 Mensuration -NCERT Solutions for Class 8 Maths Chapter 9 PDF
NCERT Solutions for Class 8 Maths Chapter 9 Mensuration
Here we have provided NCERT Solutions for Class 8 Maths Chapter 9 for the ease of students so that they can prepare better for their upcoming exams -1. A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
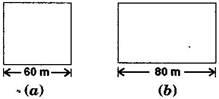
Solution:
Side of a square = 60 m (Given) And the length of the rectangular field, l = 80 m (Given) According to the question, The perimeter of the rectangular field = Perimeter of the square field 2(l+b) = 4×Side (using formulas) 2(80+b) = 4×60 160+2b = 240 b = 40 The breadth of the rectangle is 40 m. Now, the Area of the Square field = (side) 2 = (60) 2 = 3600 m 2 And the Area of the Rectangular field = length×breadth = 80×40 = 3200 m 2 Hence, the area of the square field is larger.2. Mrs.Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of Rs. 55 per m 2 .
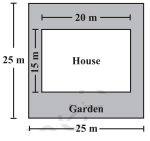
Solution:
Side of the square plot = 25 m Formula: Area of the square plot = square of the side = (side) 2 = (25) 2 = 625 Therefore the area of the square plot is 625 m 2 Length of the house = 20 m and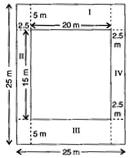
The breadth of the house = 15 m
Area of the house = length×breadth
= 20×15 = 300 m
2
Area of the garden = Area of the square plot – Area of the house
= 625–300 = 325 m
2
∵ The cost of developing the garden per sq. m is Rs. 55
The cost of developing the garden 325 sq. m = Rs. 55×325
= Rs. 17,875
Hence the total cost of developing a garden is around Rs. 17,875.
3. The shape of a garden is rectangular in the middle and semi-circular at the ends as shown in the diagram. Find the area and the perimeter of this garden [Length of rectangle is 20 – (3.5 + 3.5 meters]
Solution ::
Given: Total length = 20 m The diameter of the semi-circle = 7 m Radius of the semi-circle = 7/2 = 3.5 m Length of the rectangular field = 20-(3.5+3.5) = 20-7 = 13 m The breadth of the rectangular field = 7 m Area of rectangular field = l×b = 13×7= 91m 2 Area of the two semi-circles = 2×(1/2)×π×r 2 = 2×(1/2)×22/7×3.5×3.5 = 38.5 m 2 Area of garden = 91+38.5 = 129.5 m 2 Now, the perimeter of the two semi-circles = 2πr = 2×(22/7)×3.5 = 22 m And the perimeter of the garden = 22+13+13 = 48 m. Answer4. A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of an area of 1080 m 2 ? [If required you can split the tiles in whatever way you want to fill up the corners]
Solution:
Given: Base of flooring tile = 24 cm = 0.24 m Corresponding height of a flooring tile= 10 cm = 0.10 m Now Area of flooring tile= Base×Altitude = 0.24×0.10 = 0.024 The area of flooring tile is 0.024m 2 Number of tiles required to cover the floor= Area of floor/Area of one tile = 1080/0.024 = 45000 tiles Hence 45000 tiles are required to cover the floor.5. An ant is moving around a few food pieces of different shapes scattered on the floor. For which food piece would the ant have to take a longer round? Remember, the circumference of a circle can be obtained by using the expression C = 2πr, where r is the radius of the circle.
Solution:
(a) Radius = Diameter/2 = 2.8/2 cm = 1.4 cm
Circumference of semi-circle = πr
= (22/7)×1.4 = 4.4
The circumference of the semi-circle is 4.4 cm
Total distance covered by the ant= Circumference of semi-circle+diameter
= 4.4+2.8 = 7.2 cm
(b) Diameter of semi-circle = 2.8 cm
Radius = Diameter/2 = 2.8/2 = 1.4 cm
Circumference of semi-circle = r
= (22/7)×1.4 = 4.4 cm
Total distance covered by the ant= 1.5+2.8+1.5+4.4 = 10.2 cm
(c) Diameter of semi-circle = 2.8 cm
Radius = Diameter/2 = 2.8/2
= 1.4 cm
Circumference of semi-circle = π r
= (22/7)×1.4
= 4.4 cm
Total distance covered by the ant = 2+2+4.4 = 8.4 cm
NCERT Solutions for Class 8 Maths Chapter 9 Ex 9.2
1. The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and the perpendicular distance between them is 0.8 m.
Solution: One parallel side of the trapezium (a) = 1 m
And second side (b) = 1.2 m and height (h) = 0.8 m Area of top surface of the table= (½)×(a+b)h = (½)×(1+1.2)0.8 = (½)×2.2×0.8 = 0.88 The area of the top surface of the table is 0.88 m 2 .2. The area of a trapezium is 34 cm 2 and the length of one of the parallel sides is 10 cm and its height is 4 cm Find the length of the other parallel side.
Solution: Let the length of the other parallel side be b.
Length of one parallel side, a = 10 cm height, (h) = 4 cm and Area of a trapezium is 34 cm 2 Formula for, Area of trapezium = (1/2)×(a+b)h 34 = ½(10+b)×4 34 = 2×(10+b) After simplifying, b = 7 Hence another required parallel side is 7 cm.3. The length of the fence of a trapezium-shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m, and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.
Solution:
Given: BC = 48 m, CD = 17 m,
AD = 40 m and perimeter = 120 m
∵ Perimeter of trapezium ABCD
= AB+BC+CD+DA
120 = AB+48+17+40
120 = AB = 105
AB = 120–105 = 15 m
Now, Area of the field= (½)×(BC+AD)×AB
= (½)×(48 +40)×15
= (½)×88×15
= 660
Hence, the area of the field ABCD is 660m
2
.
4. The diagonal of a quadrilateral-shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
Solution:
Consider, h
1
= 13 m, h
2
= 8 m and AC = 24 m
Area of quadrilateral ABCD = Area of triangle ABC+Area of triangle ADC
= ½( bh
1
)+ ½(bh
2
)
= ½ ×b(h
1
+h
2
)= (½)×24×(13+8)
= (½)×24×21 = 252
Hence, the required area of the field is 252 m
2
5. The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Solution:
Given: d1 = 7.5 cm and d2 = 12 cm We know that the area of a rhombus = (½ )×d1×d2 = (½)×7.5×12 = 45 Therefore, the area of the rhombus is 45 cm 2 .6. Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of the diagonals is 8 cm long, find the length of the other diagonal.
Solution: Since a rhombus is also a kind of parallelogram,
The formula for the Area of rhombus = Base×Altitude Putting values, we have Area of rhombus = 6×4 = 24 The area of a rhombus is 24 cm 2 Also, the Formula for the Area of the rhombus = (½)×d 1 d 2 After substituting the values, we get 24 = (½)×8×d 2 d 2 = 6 Hence, the length of the other diagonal is 6 cm.7. The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2 is Rs. 4.
Solution:
Length of one diagonal, d 1 = 45 cm and d 2 = 30 cm ∵ Area of one tile = (½)d 1 d 2 = (½)×45×30 = 675 The area of one tile is 675 cm 2 An area of 3000 tiles is = 675×3000 = 2025000 cm 2 = 2025000/10000 = 202.50 m 2 [∵ 1m 2 = 10000 cm 2 ] ∵ Cost of polishing the floor per sq. meter = 4 Cost of polishing the floor per 202.50 sq. meter = 4×202.50 = 810 Hence the total cost of polishing the floor is Rs. 810.8. Mohan wants to buy a trapezium-shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m 2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
Solution:
Perpendicular distance (h) = 100 m (Given) Area of the trapezium-shaped field = 10500 m 2 (Given) Let the side along the road be ‘x’ m and the side along the river = 2x m Area of the trapezium field = (½)×(a+b)×h 10500 = (½)×(x+2x)×100 10500 = 3x×50 After simplifying, we have x = 70, which means the side along the river is 70 m Hence, the side along the river = 2x = 2( 70) = 140 m.9. The top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
Solution:
The octagon has eight equal sides, each 5 m. (given) Divide the octagon as shown in the below figure, 2 trapeziums whose parallel and perpendicular sides are 11 m and 4 m respectively, and 3 rd one is a rectangle having length and breadth of 11 m and 5 m respectively.
Now, Area of two trapeziums = 2 [(½)×(a+b)×h]
= 2×(½)×(11+5 )×4
= 4×16 = 64
Area of two trapeziums is 64 m
2
Also, the Area of the rectangle = length
= 11×5 = 55
The area of rectangle is 55 m
2
The total area of octagon = 64+55
= 119 m
2
10. There is a pentagonal-shaped park as shown in the figure.
For finding its area Jyoti and Kavita divided it in two different ways.
Find the area of this park using both ways. Can you suggest some other way of finding its area?
Solution:
First way : By Jyoti’s diagram,
Area of pentagon = Area of trapezium ABCP + Area of trapezium AEDP = (½)(AP+BC)×CP+(1/2)×(ED+AP)×DP = (½)(30+15)×CP+(1/2)×(15+30)×DP = (½)×(30+15)×(CP+DP) = (½)×45×CD = (1/2)×45×15 =337.5 m 2 Area of pentagon is 337.5 m 2Second way: By Kavita’s diagram
Here, a perpendicular AM is drawn to BE.
AM = 30–15 = 15 m
Area of pentagon = Area of triangle ABE+Area of square BCDE (from above figure)
= (½)×15×15+(15×15)
= 112.5+225.0
= 337.5
Hence, the total area of pentagon-shaped park = 337.5 m
2
11. Diagram of the adjacent picture frame has outer dimensions = 24 cm×28 cm and inner dimensions 16 cm×20 cm. Find the area of each section of the frame, if the width of each section is the same.
Solution:
Divide the given figure into 4 parts, as shown below:
Here two of the given figures (I) and (II) are similar in dimensions.
Also, figures (III) and (IV) are similar in dimensions.
Area of the figure (I) = Area of trapezium
= (½)×(a+b)×h
= (½)×(28+20)×4
= (½)×48×4 = 96
Area of figure (I) = 96 cm
2
Also, Area of Figure (II) = 96 cm
2
Now, Area of Figure (III) = Area of trapezium
= (½)×(a+b)×h
= (½)×(24+16)4
= (½)×40×4 = 80
Area of figure (III) is 80 cm
2
Also, Area of Figure (IV) = 80 cm
2
Benefits of NCERT Solutions for Class 8 Maths Chapter 9
Here are the benefits of using NCERT Solutions for Class 8 Maths Chapter 9, which covers the topic of Mensuration:Conceptual Clarity: NCERT Solutions provides detailed explanations and step-by-step solutions for problems related to mensuration. This helps students grasp the concepts of area, perimeter, and volume of different geometric shapes such as squares, rectangles, circles, triangles, cubes, cuboids, cylinders, cones, and spheres.
Practice Exercises: The solutions include a variety of practice exercises with solutions that cover different types of questions. This enables students to apply the concepts learned and develop problem-solving skills in mensuration.
Understanding Formulas: NCERT Solutions clarifies the formulas used in mensuration and demonstrates how these formulas are derived or applied in various situations. This enhances students' understanding of mathematical principles and their practical applications.
Application in Real-life Scenarios: Mensuration concepts are applicable in everyday life situations such as calculating the area of a floor, volume of a container, or perimeter of a plot. The solutions provide examples and explanations that connect mathematical concepts with real-world applications, making learning more relevant and meaningful.
Structured Learning: NCERT Solutions are structured systematically, starting from basic concepts and gradually progressing to more complex problems. This helps students build a strong foundation in mensuration and progress at their own pace.
Exam Preparation: By practicing with NCERT Solutions, students become familiar with the types of questions asked in exams and learn effective strategies to solve them. This boosts their confidence and readiness for assessments.
NCERT Solutions for Class 8 Maths Chapter 9 FAQs
How to solve mensuration problems easily class 8?
Which is the hardest chapter in class 8 maths?
What is mensuration class 8 short answer?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
