NCERT Solutions for Class 9 Maths Chapter 8:
Here we provide NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals to help students prepare for their exams. These solutions provide clear explanations and step-by-step guidance on problems related to quadrilaterals making it easier for students to grasp the concepts.
By using these solutions students can practice effectively clarify their doubts and strengthen their understanding of quadrilaterals which will be beneficial for achieving better results in their exams.
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Overview
These solutions for NCERT Class 9 Maths Chapter 8 Quadrilaterals are prepared by subject experts of Physics Wallah. They provide a detailed overview of quadrilaterals including their properties, types and various theorems related to them.
By following these solutions, students can gain a clear understanding of the chapter's concepts and learn to solve problems efficiently. The step-by-step guidance helps in building a strong foundation which is important for their exams.
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals PDF
Here we have provided NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals to assist students in their exam preparation.
By using these solutions, students can practice effectively, clear their doubts and improve their problem-solving skills which will be beneficial for achieving better results in their exams. The PDF link is available below:
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals PDF
NCERT Solutions for Class 9 Maths Chapter 8 Exercise 8.1
Below we have provided NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals-
NCERT Solutions for Class 9 Maths Chapter 8 Exercise 8.1 Page: 146
1. The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Solution:
Let the common ratio between the angles be x.
We know that the sum of the interior angles of the quadrilateral = 360°
Now,
3x+5x+9x+13x = 360°
⇒ 30x = 360°
⇒ x = 12°
, Angles of the quadrilateral are:
3x = 3×12° = 36°
5x = 5×12° = 60°
9x = 9×12° = 108°
13x = 13×12° = 156°
535
2. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution:
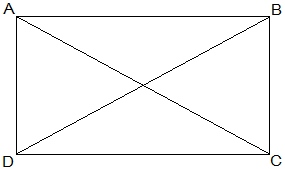Given that,
AC = BD
To show that ABCD is a rectangle if the diagonals of a parallelogram are equal
To show ABCD is a rectangle, we have to prove that one of its interior angles is right-angled.
Proof,
In ΔABC and ΔBAD,
AB = BA (Common)
BC = AD (Opposite sides of a parallelogram are equal)
AC = BD (Given)
Therefore, ΔABC ≅ ΔBAD [SSS congruency]
∠A = ∠B [Corresponding parts of Congruent Triangles]
also,
∠A+∠B = 180° (Sum of the angles on the same side of the transversal)
⇒ 2∠A = 180°
⇒ ∠A = 90° = ∠B
Therefore, ABCD is a rectangle.
Hence Proved
3. Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Solution:
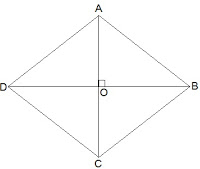Let ABCD be a quadrilateral whose diagonals bisect each other at right angles.
Given that,
OA = OC
OB = OD
and ∠AOB = ∠BOC = ∠OCD = ∠ODA = 90°
To show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus, we have to prove that ABCD is a parallelogram and AB = BC = CD = AD
Proof,
In ΔAOB and ΔCOB,
OA = OC (Given)
∠AOB = ∠COB (Opposite sides of a parallelogram are equal)
OB = OB (Common)
Therefore, ΔAOB ≅ ΔCOB [SAS congruency]
Thus, AB = BC [CPCT]
Similarly, we can prove,
BC = CD
CD = AD
AD = AB
, AB = BC = CD = AD
Opposite sides of a quadrilateral are equal. Hence, it is a parallelogram.
ABCD is rhombus as it is a parallelogram whose diagonals intersect at a right angle.
Hence Proved.
4. Show that the diagonals of a square are equal and bisect each other at right angles.
Solution:
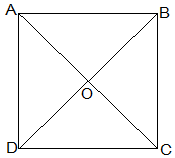Let ABCD be a square and its diagonals AC and BD intersect each other at O.
To show that,
AC = BD
AO = OC
and ∠AOB = 90°
Proof,
In ΔABC and ΔBAD,
AB = BA (Common)
∠ABC = ∠BAD = 90°
BC = AD (Given)
ΔABC ≅ ΔBAD [SAS congruency]
Thus,
AC = BD [CPCT]
diagonals are equal.
Now,
In ΔAOB and ΔCOD,
∠BAO = ∠DCO (Alternate interior angles)
∠AOB = ∠COD (Vertically opposite)
AB = CD (Given)
, ΔAOB ≅ ΔCOD [AAS congruency]
Thus,
AO = CO [CPCT].
, Diagonal bisect each other.
Now,
In ΔAOB and ΔCOB,
OB = OB (Given)
AO = CO (diagonals are bisected)
AB = CB (Sides of the square)
, ΔAOB ≅ ΔCOB [SSS congruency]
also, ∠AOB = ∠COB
∠AOB+∠COB = 180° (Linear pair)
Thus, ∠AOB = ∠COB = 90°
, Diagonals bisect each other at right angles
5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Solution:
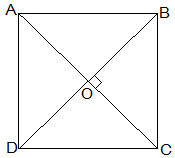Given that,
Let ABCD be a quadrilateral and its diagonals AC and BD bisect each other at a right angle at O.
To prove that,
The Quadrilateral ABCD is a square.
Proof,
In ΔAOB and ΔCOD,
AO = CO (Diagonals bisect each other)
∠AOB = ∠COD (Vertically opposite)
OB = OD (Diagonals bisect each other)
, ΔAOB ≅ ΔCOD [SAS congruency]
Thus,
AB = CD [CPCT] — (i)
also,
∠OAB = ∠OCD (Alternate interior angles)
⇒ AB || CD
Now,
In ΔAOD and ΔCOD,
AO = CO (Diagonals bisect each other)
∠AOD = ∠COD (Vertically opposite)
OD = OD (Common)
, ΔAOD ≅ ΔCOD [SAS congruency]
Thus,
AD = CD [CPCT] — (ii)
also,
AD = BC and AD = CD
⇒ AD = BC = CD = AB — (ii)
also, ∠ADC = ∠BCD [CPCT]
and ∠ADC+∠BCD = 180° (co-interior angles)
⇒ 2∠ADC = 180°
⇒∠ADC = 90° — (iii)
One of the interior angles is a right angle.
Thus, from (i), (ii) and (iii), given quadrilateral ABCD is a square.
Hence Proved.
6. Diagonal AC of a parallelogram ABCD bisects ∠A (see Fig. 8.19). Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
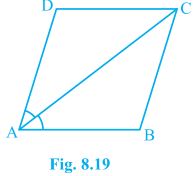
Solution:
(i) In ΔADC and ΔCBA,
AD = CB (Opposite sides of a parallelogram)
DC = BA (Opposite sides of a parallelogram)
AC = CA (Common Side)
, ΔADC ≅ ΔCBA [SSS congruency]
Thus,
∠ACD = ∠CAB by CPCT
and ∠CAB = ∠CAD (Given)
⇒ ∠ACD = ∠BCA
Thus,
AC bisects ∠C also.
(ii) ∠ACD = ∠CAD (Proved above)
⇒ AD = CD (Opposite sides of equal angles of a triangle are equal)
Also, AB = BC = CD = DA (Opposite sides of a parallelogram)
Thus,
ABCD is a rhombus.
7. ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
Solution:
Given that,
ABCD is a rhombus.
AC and BD are its diagonals.
Proof,
AD = CD (Sides of a rhombus)
∠DAC = ∠DCA (Angles opposite of equal sides of a triangle are equal.)
also, AB || CD
⇒∠DAC = ∠BCA (Alternate interior angles)
⇒∠DCA = ∠BCA
, AC bisects ∠C.
Similarly,
We can prove that diagonal AC bisects ∠A.
Following the same method,
We can prove that the diagonal BD bisects ∠B and ∠D.
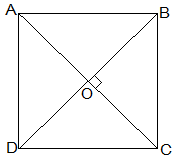
8. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
(i) ABCD is a square
(ii) Diagonal BD bisects ∠B as well as ∠D.
Solution:
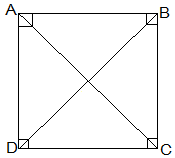(i) ∠DAC = ∠DCA (AC bisects ∠A as well as ∠C)
⇒ AD = CD (Sides opposite to equal angles of a triangle are equal)
also, CD = AB (Opposite sides of a rectangle)
,AB = BC = CD = AD
Thus, ABCD is a square.
(ii) In ΔBCD,
BC = CD
⇒ ∠CDB = ∠CBD (Angles opposite to equal sides are equal)
also, ∠CDB = ∠ABD (Alternate interior angles)
⇒ ∠CBD = ∠ABD
Thus, BD bisects ∠B
Now,
∠CBD = ∠ADB
⇒ ∠CDB = ∠ADB
Thus, BD bisects ∠B as well as ∠D.
9. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig. 8.20). Show that:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ is a parallelogram
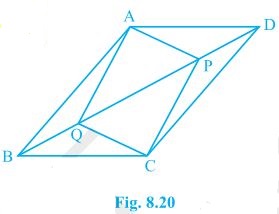
Solution:
(i) In ΔAPD and ΔCQB,
DP = BQ (Given)
∠ADP = ∠CBQ (Alternate interior angles)
AD = BC (Opposite sides of a parallelogram)
Thus, ΔAPD ≅ ΔCQB [SAS congruency]
(ii) AP = CQ by CPCT as ΔAPD ≅ ΔCQB.
(iii) In ΔAQB and ΔCPD,
BQ = DP (Given)
∠ABQ = ∠CDP (Alternate interior angles)
AB = CD (Opposite sides of a parallelogram)
Thus, ΔAQB ≅ ΔCPD [SAS congruency]
(iv) As ΔAQB ≅ ΔCPD
AQ = CP [CPCT]
(v) From the questions (ii) and (iv), it is clear that APCQ has equal opposite sides and also has equal and opposite angles. , APCQ is a parallelogram.
10. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.21). Show that
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
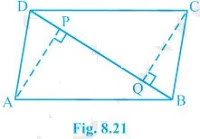
Solution:
(i) In ΔAPB and ΔCQD,
∠ABP = ∠CDQ (Alternate interior angles)
∠APB = ∠CQD (= 90
o
as AP and CQ are perpendiculars)
AB = CD (ABCD is a parallelogram)
, ΔAPB ≅ ΔCQD [AAS congruency]
(ii) As ΔAPB ≅ ΔCQD.
, AP = CQ [CPCT]
11. In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F, respectively (see Fig. 8.22).
Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ΔABC ≅ ΔDEF.
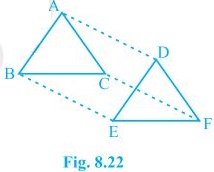
Solution:
(i) AB = DE and AB || DE (Given)
Two opposite sides of a quadrilateral are equal and parallel to each other.
Thus, quadrilateral ABED is a parallelogram
(ii) Again BC = EF and BC || EF.
Thus, quadrilateral BEFC is a parallelogram.
(iii) Since ABED and BEFC are parallelograms.
⇒ AD = BE and BE = CF (Opposite sides of a parallelogram are equal)
, AD = CF.
Also, AD || BE and BE || CF (Opposite sides of a parallelogram are parallel)
, AD || CF
(iv) AD and CF are opposite sides of quadrilateral ACFD which are equal and parallel to each other. Thus, it is a parallelogram.
(v) Since ACFD is a parallelogram
AC || DF and AC = DF
(vi) In ΔABC and ΔDEF,
AB = DE (Given)
BC = EF (Given)
AC = DF (Opposite sides of a parallelogram)
, ΔABC ≅ ΔDEF [SSS congruency]
12. ABCD is a trapezium in which AB || CD and AD = BC (see Fig. 8.23). Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
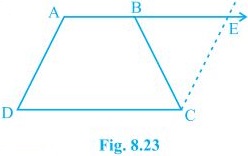
Solution:
To Construct: Draw a line through C parallel to DA intersecting AB produced at E.
(i) CE = AD (Opposite sides of a parallelogram)
AD = BC (Given)
, BC = CE
⇒∠CBE = ∠CEB
also,
∠A+∠CBE = 180° (Angles on the same side of transversal and ∠CBE = ∠CEB)
∠B +∠CBE = 180° ( As Linear pair)
⇒∠A = ∠B
(ii) ∠A+∠D = ∠B+∠C = 180° (Angles on the same side of transversal)
⇒∠A+∠D = ∠A+∠C (∠A = ∠B)
⇒∠D = ∠C
(iii) In ΔABC and ΔBAD,
AB = AB (Common)
∠DBA = ∠CBA
AD = BC (Given)
, ΔABC ≅ ΔBAD [SAS congruency]
(iv) Diagonal AC = diagonal BD by CPCT as ΔABC ≅ ΔBAD.
NCERT Solutions for Class 9 Maths Chapter 8 Exercise 8.1 Page: 150
1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see Fig 8.29). AC is a diagonal. Show that:
(i) SR || AC and SR = 1/2 AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Solution:
(i) In ΔDAC,
R is the mid point of DC and S is the mid point of DA.
Thus by mid point theorem, SR || AC and SR = ½ AC
(ii) In ΔBAC,
P is the mid point of AB and Q is the mid point of BC.
Thus by mid point theorem, PQ || AC and PQ = ½ AC
also, SR = ½ AC
, PQ = SR
(iii) SR || AC ———————- from question (i)
and, PQ || AC ———————- from question (ii)
⇒ SR || PQ – from (i) and (ii)
also, PQ = SR
, PQRS is a parallelogram.
2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
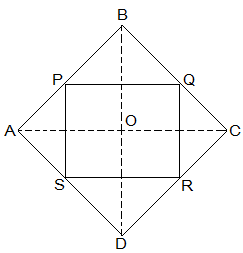Given in the question,
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively.
To Prove,
PQRS is a rectangle.
Construction,
Join AC and BD.
Proof:
In ΔDRS and ΔBPQ,
DS = BQ (Halves of the opposite sides of the rhombus)
∠SDR = ∠QBP (Opposite angles of the rhombus)
DR = BP (Halves of the opposite sides of the rhombus)
, ΔDRS ≅ ΔBPQ [SAS congruency]
RS = PQ [CPCT]———————- (i)
In ΔQCR and ΔSAP,
RC = PA (Halves of the opposite sides of the rhombus)
∠RCQ = ∠PAS (Opposite angles of the rhombus)
CQ = AS (Halves of the opposite sides of the rhombus)
, ΔQCR ≅ ΔSAP [SAS congruency]
RQ = SP [CPCT]———————- (ii)
Now,
In ΔCDB,
R and Q are the mid points of CD and BC, respectively.
⇒ QR || BD
also,
P and S are the mid points of AD and AB, respectively.
⇒ PS || BD
⇒ QR || PS
, PQRS is a parallelogram.
also, ∠PQR = 90°
Now,
In PQRS,
RS = PQ and RQ = SP from (i) and (ii)
∠Q = 90°
, PQRS is a rectangle.
3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
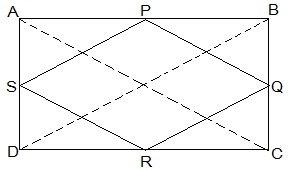Given in the question,
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA, respectively.
Construction,
Join AC and BD.
To Prove,
PQRS is a rhombus.
Proof:
In ΔABC
P and Q are the mid-points of AB and BC, respectively
, PQ || AC and PQ = ½ AC (Midpoint theorem) — (i)
In ΔADC,
SR || AC and SR = ½ AC (Midpoint theorem) — (ii)
So, PQ || SR and PQ = SR
As in quadrilateral PQRS one pair of opposite sides is equal and parallel to each other, so, it is a parallelogram.
, PS || QR and PS = QR (Opposite sides of parallelogram) — (iii)
Now,
In ΔBCD,
Q and R are mid points of side BC and CD, respectively.
, QR || BD and QR = ½ BD (Midpoint theorem) — (iv)
AC = BD (Diagonals of a rectangle are equal) — (v)
From equations (i), (ii), (iii), (iv) and (v),
PQ = QR = SR = PS
So, PQRS is a rhombus.
Hence Proved
4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
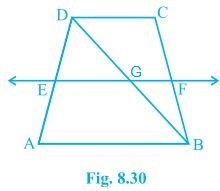
Solution:
Given that,
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD.
To prove,
F is the mid-point of BC.
Proof,
BD intersected EF at G.
In ΔBAD,
E is the mid point of AD and also EG || AB.
Thus, G is the mid point of BD (Converse of mid point theorem)
Now,
In ΔBDC,
G is the mid point of BD and also GF || AB || DC.
Thus, F is the mid point of BC (Converse of mid point theorem)
5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD, respectively (see Fig. 8.31). Show that the line segments AF and EC trisect the diagonal BD.
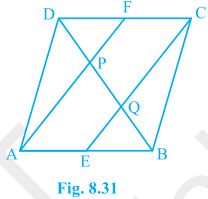
Solution:
Given that,
ABCD is a parallelogram. E and F are the mid-points of sides AB and CD, respectively.
To show,
AF and EC trisect the diagonal BD.
Proof,
ABCD is a parallelogram
, AB || CD
also, AE || FC
Now,
AB = CD (Opposite sides of parallelogram ABCD)
⇒½ AB = ½ CD
⇒ AE = FC (E and F are midpoints of side AB and CD)
AECF is a parallelogram (AE and CF are parallel and equal to each other)
AF || EC (Opposite sides of a parallelogram)
Now,
In ΔDQC,
F is mid point of side DC and FP || CQ (as AF || EC).
P is the mid-point of DQ (Converse of mid-point theorem)
⇒ DP = PQ — (i)
Similarly,
In ΔAPB,
E is midpoint of side AB and EQ || AP (as AF || EC).
Q is the mid-point of PB (Converse of mid-point theorem)
⇒ PQ = QB — (ii)
From equations (i) and (i),
DP = PQ = BQ
Hence, the line segments AF and EC trisect the diagonal BD.
Hence Proved.
6
.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Solution:
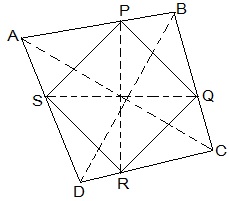Let ABCD be a quadrilateral and P, Q, R and S the mid points of AB, BC, CD and DA, respectively.
Now,
In ΔACD,
R and S are the mid points of CD and DA, respectively.
, SR || AC.
Similarly we can show that,
PQ || AC,
PS || BD and
QR || BD
, PQRS is parallelogram.
PR and QS are the diagonals of the parallelogram PQRS. So, they will bisect each other.
7. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = ½ AB
Solution:
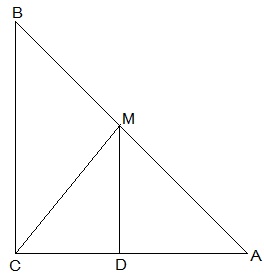(i) In ΔACB,
M is the midpoint of AB and MD || BC
, D is the midpoint of AC (Converse of mid point theorem)
(ii) ∠ACB = ∠ADM (Corresponding angles)
also, ∠ACB = 90°
, ∠ADM = 90° and MD ⊥ AC
(iii) In ΔAMD and ΔCMD,
AD = CD (D is the midpoint of side AC)
∠ADM = ∠CDM (Each 90°)
DM = DM (common)
, ΔAMD ≅ ΔCMD [SAS congruency]
AM = CM [CPCT]
also, AM = ½ AB (M is midpoint of AB)
Hence, CM = MA = ½ AB
Benefits of NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals
-
Clear Understanding of Concepts:
These solutions help students gain a clear understanding of the various properties and theorems related to quadrilaterals. By studying these solutions, students can grasp the fundamentals of quadrilaterals making it easier to solve related problems.
-
Step-by-Step Solutions:
The solutions provide a step-by-step approach to solving problems making it easier for students to follow and understand the methodology. This detailed explanation helps in building a strong foundation in geometry.
-
Effective Exam Preparation:
Using these solutions students can effectively prepare for their exams. The solutions cover all the important questions from the chapter ensuring that students are well-prepared for any type of question that may appear in the exams.
-
Doubt Clarification:
These solutions are designed to clear any doubts students may have while solving problems related to quadrilaterals. By referring to these solutions, students can get their doubts resolved and strengthen their understanding of the topic.
-
Time Management:
By practicing with these solutions, students can learn to manage their time effectively during exams. The step-by-step approach helps in solving problems more efficiently, allowing students to complete their exams within the given time frame.
