Refractive Index
Sep 26, 2022, 16:45 IST
The
Refractive Index
is the ratio between a speed of light in a medium and the speed in a vacuum. When the light travels in a medium other than a vacuum, the atoms of that medium constantly absorb and re-emit particles of light, slowing down the speed of light. In this short topic, we will go through the refractive index of water and different media.
The
Refractive Index
is defined as
"Ratio of the speed of light in a specific medium to the speed in a vacuum."
The Refractive index is referred to as the refraction index or index of refraction. The speed of light in a medium depends on the properties of the medium. For electromagnetic waves, the speed depends on the optical density of the medium. Optical density is the tendency of atoms in a material to recover absorbed electromagnetic energy. The optically denser the material, the slower the speed of light. One such indicator of the optical density of a medium is the refractive index.
The refractive index is dimensionless. It's a number that tells how much slower a light wave is in the material than it is in a vacuum. The refractive index represented by "n" is the ratio of the speed of light in a vacuum to the speed of light in the medium. The refractive index formula is as follows:
n = c/v
where
n = refractive index of the medium
c = speed of light when in vacuum ( 3 × 10
8
m/s)
v = speed of light when in medium
The vacuum has a refractive index of 1. The refractive index of other materials can be determined from the given equation above. The higher the refractive index, also the higher the optical density and slow the speed of light.
|
Material
|
Refractive Index
|
|
Air
|
1.0003
|
|
Water
|
1.333
|
|
Diamond
|
2.417
|
|
Ice
|
1.31
|
|
Ethyl Alcohol
|
1.36
|
The Phenomenon of Refraction Deals with two aspects -
-
Angle of Refraction
-
Speed of the light in the medium
The index of refraction or refractive index also determines how much light changes its path as it passes from one medium to another. This angle of refraction explains Snell's law. It is also known as the "law of refraction" and the "Snell-Descartes" law. Willebrord Snell discovered Snell's law in 1621.
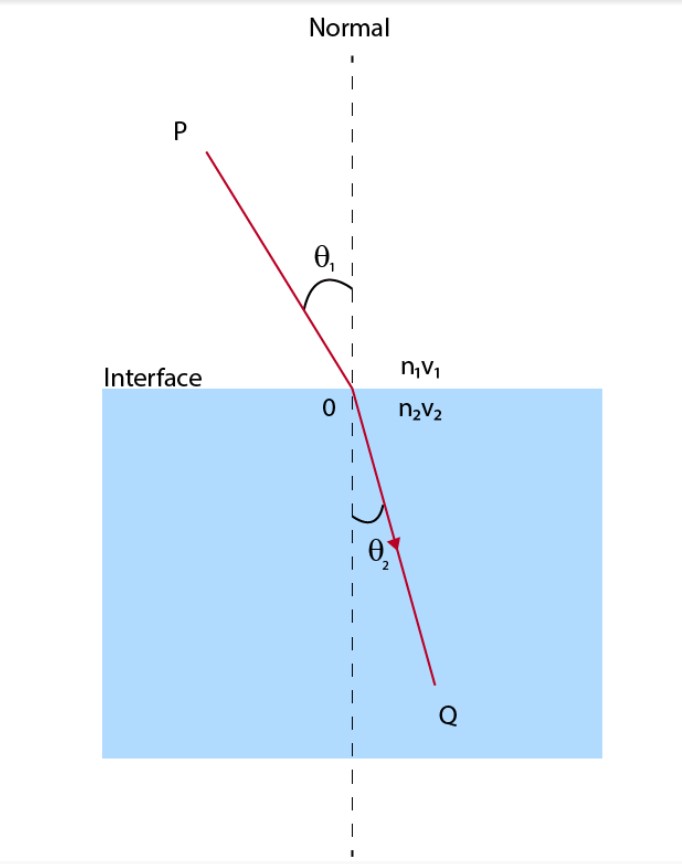
When light hits a barrier between two mediums, the light is partially refracted and reflected. Snell's law explains the relationship between the angle of incidence and the angle of refraction when the light passes from one medium to another, such as air, glass, or water.
The ratio of the sine angle of incidence and the sine angle of refraction is the same as the ratio of the phase velocity in two different mediums. Moreover, it is identical to the ratio of refractive indices.
Sinθ
2
/ Sinθ
1
= v
2
/v
1
= n
1
/n
2
Here,
-
θ is determined from the line perpendicular to the boundary of the surface
-
v = Velocity of light with respect to each medium
-
n = Refractive index with respect to each medium
To find the refractive index, the speed of light is considered in two mediums. The symbol "n" denotes the refractive index.
Speed of Light in the 1st Medium = v
1
Speed of light in the 2nd Medium = v
2
Thus, the refractive index (n) of the 2nd Medium with respect to the 1st medium is:
n
21
= Speed of Light in 1st medium/ Speed of light in 2nd Medium
Or,
n
21
= v1/v2
Therefore, the refractive index (n) of 1st Medium with respect to 2nd Medium is:
n
12
= Speed of Light in 2nd medium/ Speed of light in 1st medium
Or,
n
12
= v
2
/ v
1
Q1. A ray of light is transient through a medium to another medium. The angle of the incident comes out to be 30 degrees. Also, the angle of refraction happens to be 50 degrees. Find out the refractive index of the second medium.
Ans.
The parameters which are known are
The angle of incidence (‘i’) = 30 degrees
The angle of refraction (‘r’) = 50 degrees
The refractive index formula is as follows
n = sini / sinr
n = sin30/sin50
n = 0.50.766 = 0.6527
Q2. Find the refractive index of the medium such that the speed of light in the medium is 2 × 108 m/s.
Ans.
Given,
Speed of light in the vacuum (c) = 3×108m/s
Speed of light in the medium (v) = 2×108m/s
Now, one must apply the formula of refractive index,
Q1. What can affect the refractive index?
Ans.
The two factors which affect the value of the refractive index are:
-
Temperature
-
Wavelength of light
Q2. What is the purpose of refractive index?
Ans.
The purpose of refractive index is used to measures solids, liquids, and gases. Generally, it is used to measure the concentration of a solute in an aqueous solution.
Q3. Is there a limit to refractive index?
Ans.
Accordingly, despite the giant response of an isolated atom, we find that the maximum index does not indefinitely grow with increasing density but rather reaches a limiting value of
n≈1.7
.
Q4. What is the refractive index of water?
Ans.
The refractive index of water is
1.333.
Q5. How to find Refractive index?
Ans.
Refractive index is equal to the velocity of light c of a given wavelength in empty space divided by its velocity v in a substance, or
n = c/v
.
