
The potential energy curve for an object in a conservative force field, such as gravitational or electric, can be described using the following formula:
 U(r) = -G * (m1 * m2) / r
In this formula:
- U(r) represents the potential energy at a distance r from the center of the field.
- G is the gravitational constant (approximately 6.674 × 10^-11 N(m/kg)^2 for gravitational potential energy).
- m1 and m2 are the masses of the two objects (for gravitational potential energy, such as the Earth and an object near its surface, m1 is the mass of the Earth, and m2 is the mass of the object).
- r is the distance between the centers of the two objects.
U(r) = -G * (m1 * m2) / r
In this formula:
- U(r) represents the potential energy at a distance r from the center of the field.
- G is the gravitational constant (approximately 6.674 × 10^-11 N(m/kg)^2 for gravitational potential energy).
- m1 and m2 are the masses of the two objects (for gravitational potential energy, such as the Earth and an object near its surface, m1 is the mass of the Earth, and m2 is the mass of the object).
- r is the distance between the centers of the two objects.
Also Check - Unit, Dimension & Vector Formula
This formula applies to the gravitational potential energy. For electric potential energy in an electrostatic field, you can use a similar formula with Coulomb's constant (k) instead of the gravitational constant and the charges (q1 and q2) instead of masses (m1 and m2): U(r) = k * (q1 * q2) / r In this formula: - U(r) represents the electric potential energy at a distance r from a point charge. - k is Coulomb's constant (approximately 8.988 × 10^9 N(m^2/C^2)). - q1 and q2 are the magnitudes of the electric charges. These formulas describe the potential energy between two objects in a conservative force field as a function of their separation distance. As the distance between the objects changes, the potential energy also changes, and the curve representing this relationship can be plotted. Typically, potential energy decreases as objects move farther apart and increases as they move closer together.Also Check - Work, Energy & Power Formula
Curve
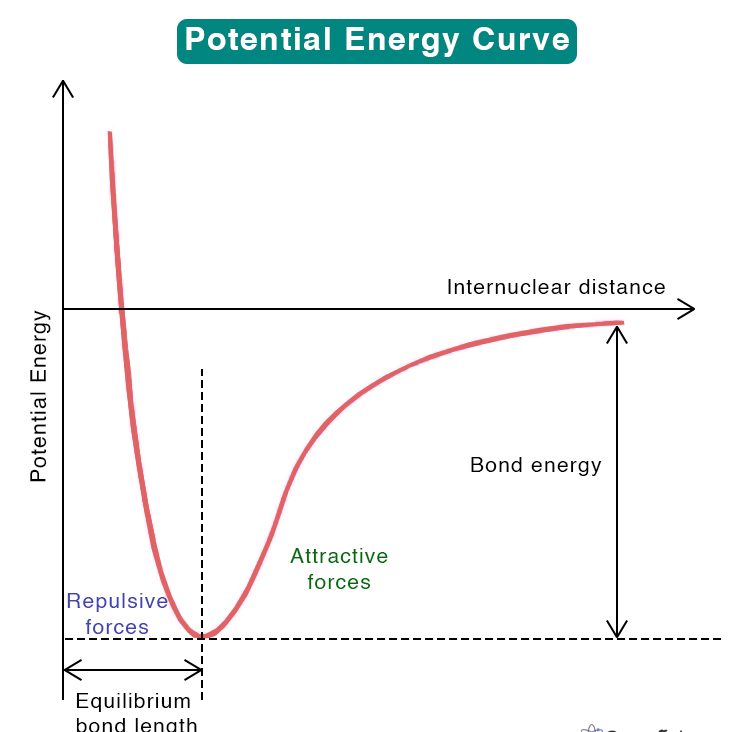
A potential energy curve, often referred to as a potential energy surface (PES), is a graphical representation of the potential energy of a system as a function of its configuration or coordinates. In physics and chemistry, it is a fundamental concept used to analyze and understand the behavior of molecules, atoms, and other systems. The key idea is that the potential energy of a system depends on the positions and orientations of its constituent particles. Here's a general idea of what a potential energy curve represents:- X-Axis: The horizontal axis typically represents one or more coordinates or parameters that describe the configuration or state of the system. For example, in a simple diatomic molecule, the x-axis might represent the bond length (the distance between the two atoms).
- Y-Axis: The vertical axis represents the potential energy of the system. This is the energy associated with the arrangement of particles in the given configuration.
- Curve Shape: The shape of the curve illustrates how the potential energy changes as the system's configuration changes. The curve can have one or more minima (lowest points), which correspond to stable configurations of the system, and maxima (highest points), which correspond to less stable or transition states.
Also Check - Thermodynamics Formula
Different Potential Energy Curves
In the context of physics, a potential energy curve represents the potential energy of a system, often as a function of the position of an object or the configuration of a system. It is a graphical way to visualize how the potential energy of a system changes with respect to a specific variable, such as position or displacement. Here are some common examples in physics where potential energy curves are used:- Gravitational Potential Energy Curve : In the case of an object near the Earth's surface, the potential energy curve is typically a U-shaped curve, where the minimum point represents the lowest potential energy when the object is at the ground level. As you move upward or downward, the potential energy increases.
- Spring Potential Energy Curve: When dealing with a spring-mass system, the potential energy curve is parabolic. The minimum point represents the equilibrium position of the mass, where the spring is neither stretched nor compressed. As you displace the mass from this position, the potential energy increases quadratically.
- Atomic and Molecular Potential Energy Surfaces : In quantum mechanics, potential energy surfaces are used to describe the energy of electrons and nuclei in molecules. These surfaces can be highly complex, with multiple minima and maxima, and they are crucial for understanding molecular bonding, chemical reactions, and spectroscopy.
- Nuclear Potential Energy Curve : In nuclear physics, the potential energy curve for a nucleus can be used to understand nuclear stability, fusion, and fission processes. The curve may exhibit various features, including a potential energy well at certain nuclear sizes.
Also Check - Work Done in Raising a Box Formula
These potential energy curves provide valuable insights into the behavior of physical systems. They help physicists analyze and predict how objects and particles will move and interact in response to forces or changes in their surroundings, based on the principles of potential energy and conservation of energy. When discussing potential energy (PE) with respect to displacement in physics, we are often referring to a situation where an object's potential energy changes as it moves within a force field, such as gravitational potential energy or elastic potential energy due to a spring. In these cases, the potential energy depends on the object's position or displacement from a reference point.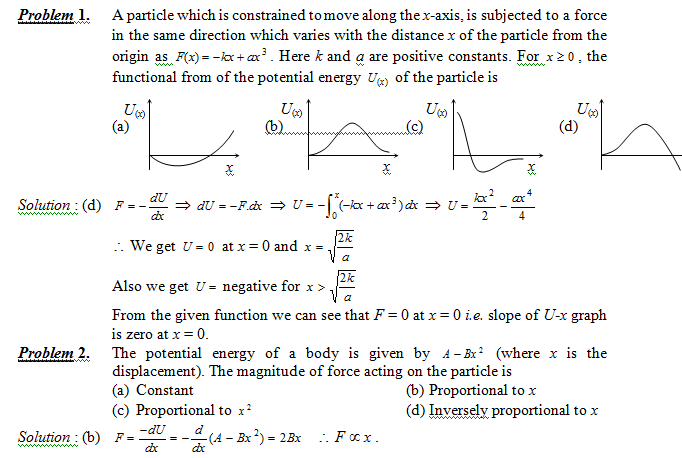
Here are two common examples Potential Energy :
- Gravitational Potential Energy (GPE): Gravitational potential energy is the energy associated with the height or vertical displacement of an object in a gravitational field, such as near the Earth's surface. The formula for gravitational potential energy is:
Also Check - Work Done by a Variable Force
- Elastic Potential Energy (EPE): Elastic potential energy is the energy stored in a stretched or compressed spring or elastic material. The formula for elastic potential energy is:
Potential Energy Curve Formula FAQs
What is potential energy, and how does it relate to displacement?
Potential energy is the stored energy an object has due to its position within a force field. It relates to displacement by quantifying how much an object's energy changes as it moves from one position to another within that force field.
Why does gravitational potential energy increase with height?
Gravitational potential energy increases with height because the force of gravity acts in the opposite direction of displacement. As you lift an object higher against gravity, you do work on it, and this work is stored as potential energy.
In the context of elastic potential energy, what happens to the energy as you stretch a spring further from its equilibrium position?
When you stretch a spring further from its equilibrium position, the elastic potential energy increases. This is because you are doing work on the spring to deform it from its relaxed state, and this work is stored as potential energy in the spring.
Can potential energy ever be negative?
Yes, potential energy can be negative. It depends on the reference point chosen for calculating potential energy. For example, when calculating gravitational potential energy near the Earth's surface, if the reference point is chosen at a higher elevation than the object, the potential energy can be negative for objects below that reference point.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App









