
RS Aggarwal Solutions for Class 8 Maths Chapter 13 Exercise 13.1: RS Aggarwal Solutions for Class 8 Maths Chapter 13 Exercise 13.1 focus on the concept of Time and Work. This exercise helps students understand how to calculate the time required to complete tasks based on different work rates.
It covers problems where students need to determine the time taken by individuals or groups to finish a job and how working together affects the overall time. The solutions provide clear, step-by-step explanations helping students grasp the relationship between time, work and efficiency. By working through these exercises students enhance their ability to solve real-life problems related to time management and work efficiency.RS Aggarwal Solutions for Class 8 Maths Chapter 13 Exercise 13.1 Overview
RS Aggarwal Solutions for Class 8 Maths Chapter 13 Exercise 13.1 PDF
RS Aggarwal Solutions for Class 8 Maths Chapter 13 Exercise 13.1 PDF is available below. This document provides comprehensive solutions to the exercise problems, which cover various aspects of Time and Work. It includes step-by-step explanations to help students understand how to calculate work rates, determine time required for task completion, and solve related problems effectively. Access the PDF to enhance your understanding and get detailed guidance on tackling these exercises.RS Aggarwal Solutions for Class 8 Maths Chapter 13 Exercise 13.1 PDF
RS Aggarwal Solutions for Class 8 Maths Chapter 13 Exercise 13.1 (Ex 13A)
RS Aggarwal Solutions for Class 8 Maths Chapter 13 Exercise 13.1 are available below. This resource provide detailed solutions and explanations for problems related to Direct and Inverse Proportions.(Question 1) Rajan can do piece of work in 24 days while Amit can do it in 30 days. In how many days can they complete it, if they work together?
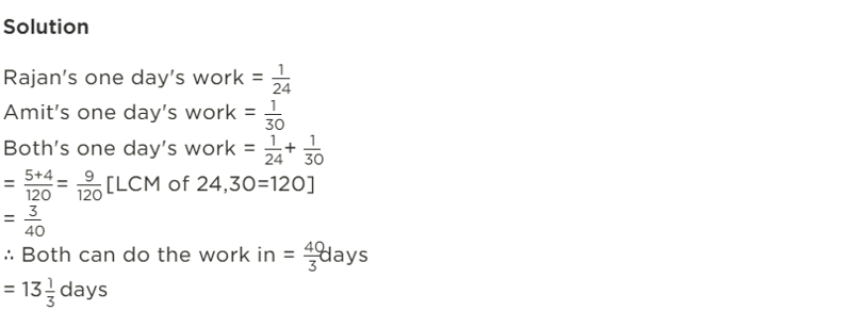
(Question 2) Ravi can do a piece of work in 15 hours while Raman can do it in 12 hours. How long will both take to do it, working together?
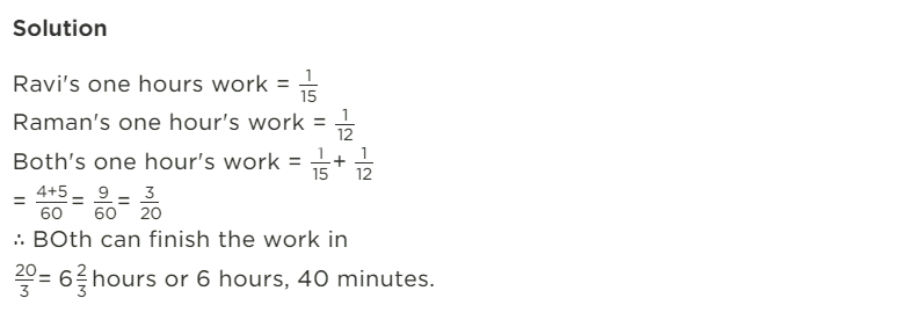
(Question 3) A and B, working together can finish a piece of work in 6 days, while A alone can do it in 9 days. How much time will B alone take to finish it?
Solution:
(Question 4) Two motor mechanics, Raju and Siraj, working together can overhaul a scooter in 6 hours. Raju alone can do the job in 15 hours. In how many hours can Siraj alone do it?
Solution:
We know that, Number of hours raju requires to do the job = 15 hours(Question 5) A, B and C can do a piece of work in 10 days, 12 days and 15 days respectively. How long will they take to finish it if they work together?
Solution:
We know that, Number of days A requires to do piece of work = 10 days Number of days B requires to do the piece of work = 12 days Number of days C requires to do the piece of work = 15 days ∴ We can calculate, work done by A in 1 day = 1 / 10 Work done by B in 1 day = 1 / 12 Work done by C in 1 day = 1 / 15 Now, work done by A , B and C together in 1 day = 1 / 10 + 1 / 12 + 1 / 15 = 15 / 60 = 1 / 4 ∴ They can do work together in 4 days.(Question 6) A can do a piece of work in 24 hours while B alone can do it in 16 hours. If A, B and C working together can finish it in 8 hours, in how many hours can C alone finish the work?
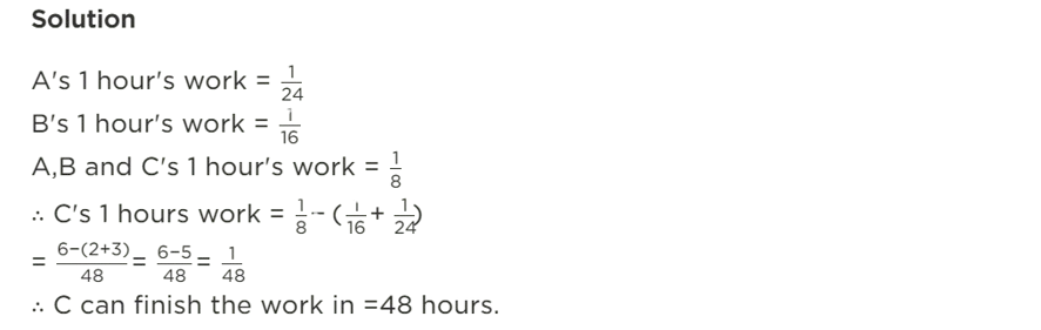
(Question 7) A, B and C working together can finish a piece of work in 8 hours. A alone can do it in 20 hours and B alone can do it in 24 hours. In how many hours will C alone do the same work?
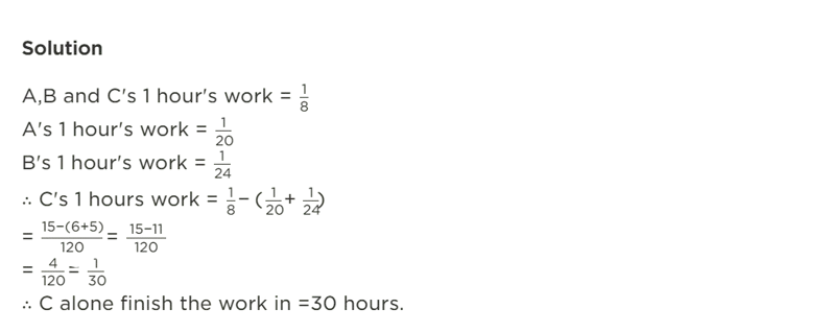
(Question 8) A and B can finish a piece of work in 16 days and 12 days respectively. A started the work and worked at it for 2 days. He was then joined by B. Find the total time taken to finish the work.
Solution:
We know that, Number of days A required to do piece of work = 16 days Number of days B required to do piece of work = 12 days ∴ We can calculate, work done by A in 1 day = 1 / 16 Work done by B in 1 day = 1 / 12 A alone works for 2 days so, the amount of work completed by A in 2 days = 2 × 1 / 16 = 1 / 8 ∴ work left = 1 − 1 / 8 = 7 / 8 Work done by A , B together in a one day = 1 / 16 + 1 / 12 = 7 / 48 ∴ they can complete the work together in 48 / 7 days But only 7 / 8 t h of work is to be completed by both A and B ∴ time required to complete 7 / 8 t h work together by A and B = 7 / 8 × 48 / 7 = 6 days Time taken to finish the work = 6 + 2 = 8 days ( 2 is added because 1 / 8 work is done by A alone) ∴ Total time taken to complete the work = 8 days.(Question 9) A can do a piece of work in 14 days and B can do it in 21 days. They began together and worked at it for 6 days. Then, A fell ill and B had to complete the remaining work alone. In how many days was the work completed?
Solution:
A can do a piece of work in 14 days. Therefore A ′ s one days work will be 1 14 B can do a piece of work in 21 days.(Question 10) A can do 2/3 of a certain work in 16 days and B can do ¼ of the same work in 3 days. In how many days can both finish the work, working together?
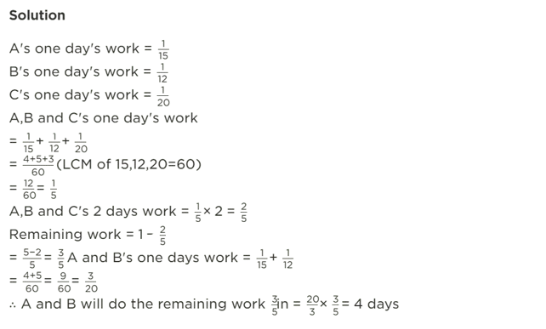
(Question 12) A and B can do a piece of work in 18 days; B and C can do it in 24 days while C and A can finish it in 36 days. In how many days can A, B, C finish it, if they all work together?
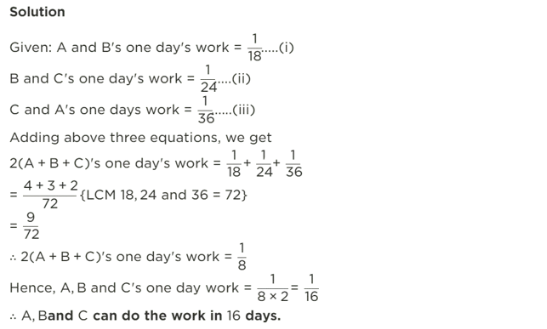
Benefits of RS Aggarwal Solutions for Class 8 Maths Chapter 13 Exercise 13.1
- Comprehensive Understanding : The solutions provide detailed explanations and step-by-step guidance for each problem, helping students grasp the underlying concepts of Time and Work effectively.
- Problem-Solving Skills : By practicing these solutions students can enhance their ability to solve various types of time and work problems, improving their problem-solving skills and confidence.
- Clarity of Concepts : The solutions clarify complex concepts and formulas related to time and work, making it easier for students to understand and apply them in different scenarios.
- Exam Preparation : Regular practice with these solutions helps students become familiar with the types of questions that may appear in exams leading to better preparation and performance.
- Error Correction : The detailed solutions help students identify and correct their mistakes, fostering a better understanding of how to approach and solve similar problems in the future.
- Time Management : Through these solutions students learn to manage their time efficiently while solving problems, which is important for performing well in timed exams.
RS Aggarwal Solutions for Class 8 Maths Chapter 13 Exercise 13.1 FAQs
What is the focus of Exercise 13.1 in Chapter 13 of RS Aggarwal’s Class 8 Maths?
How can I effectively use the RS Aggarwal solutions for Exercise 13.1?
What concepts are important for solving Exercise 13.1?
How can these solutions help in exam preparation?









