Wave Motion Formula - Definition, Classification, Characteristics

Wave motion formula , often simply referred to as waves, is a fundamental and pervasive phenomenon found throughout the natural world. It involves the propagation of energy through a medium without the physical movement of matter over long distances. Waves exhibit a diverse range of behaviours and can be observed in various forms, from the ripples on the surface of water to the vibrations of sound and light.

What is Wave Motion?

Wave motion, also known simply as waves, is a fundamental concept in physics and refers to the transfer of energy through a medium without the physical displacement of the medium itself. In other words, waves carry energy from one place to another without the particles of the medium actually travelling the entire distance.

Also Check - Friction Formula

Wave Equation

The wave equation describes the propagation of waves, such as electromagnetic waves or mechanical waves, in one dimension (typically along a single axis like the x-axis).

The equation is given by

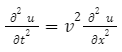
Where,

1. u is the displacement of the wave at a point.
2. t is time.
3. x is the position along the axis.
4. v is the wave velocity.

Also Check - Elasticity Formula

Classification of Wave Motion Formula

Wave motion can be classified into different categories based on various characteristics and properties of the waves. The classification of wave motion includes:

Mechanical Waves vs. Electromagnetic Waves:

• Mechanical Waves: These waves can only travel through a solid, liquid, or gas. Examples include earthquakes, water, and sound waves.
• Electromagnetic Waves: These waves can go across a vacuum and don't need a medium to do so. Light, radio waves, microwaves, and X-rays are a few examples.

Transverse Waves vs. Longitudinal Waves:

• Transverse Waves: In transverse waves, the particle displacement is perpendicular to the direction of wave propagation. Examples include light waves and water waves.
• Longitudinal Waves: In longitudinal waves, the particle displacement is parallel to the direction of wave propagation. Sound and seismic waves are two examples.

Surface Waves vs. Body Waves:

• Surface Waves: These waves travel along the boundary between two different media. They include water waves, Love waves (in seismology), and surface plasmon waves.
• Body Waves: These waves move through a medium's interior. In seismology, they are referred to as P-waves (primary or compressional waves) and S-waves (secondary or shear waves).

Progressive Waves vs. Standing Waves:

• Progressive Waves: These waves move forward and carry energy from one point to another. Ocean waves and sound waves are examples.
• Standing Waves: Due to the interference of two similar waves moving in the opposite directions, these waves appear to "stand still." They occur in confined spaces and are seen in musical instruments (e.g., strings, pipes).

One-Dimensional, Two-Dimensional, and Three-Dimensional Waves:

• One-Dimensional Waves: These waves propagate along a single dimension (e.g., along a rope).
• Two-Dimensional Waves: These waves propagate in a plane or on a surface (e.g., water waves on the surface of a pond).
• Three-Dimensional Waves: These waves propagate in three-dimensional space (e.g., sound waves in air).

Continuous Waves vs. Discrete Waves:

• Continuous Waves: These waves are continuous and propagate indefinitely, such as sound waves and electromagnetic waves.
• Discrete Waves: These waves consist of a series of distinct pulses or wave packets, such as water waves resulting from throwing a stone into a pond.

Linear Waves vs. Nonlinear Waves:

• Linear Waves: These waves follow the principle of superposition, where the combined effect of multiple waves is the algebraic sum of their individual effects.
• Nonlinear Waves: These waves do not obey the principle of superposition and can exhibit complex behaviours, such as solitons and rogue waves.

These classifications help organise and understand the different types of waves and their properties. Waves are a fundamental aspect of the natural world and play a significant role in various scientific disciplines and technological applications.

Also Check - Gravitational Force Formula

Periodic and Non-Periodic Waves

Periodic Waves

Periodic waves are waves that exhibit a regular and repetitive pattern of oscillation over time. This means that the wave pattern repeats itself at regular intervals. The key characteristic of a periodic wave is that it has a well-defined period (or frequency), amplitude, and wavelength.

• Period: The length of time it takes for one oscillation (cycle) to complete determines a wave's period ( T ). Periodic waves have a consistent and predictable period.
• Frequency: The frequency (f) of a periodic wave is the number of complete oscillations that occur in a unit of time. It is the reciprocal of the period: f= 1/ T

Non-Periodic Waves

Non-periodic waves, also known as aperiodic waves, do not exhibit a regular or repeating pattern of oscillation over time. The wave pattern may change irregularly and unpredictably, making it difficult to define a specific period, frequency, or wavelength.

Characteristics of Wave Motion Formula

Wave motion exhibits several key characteristics that help define and differentiate different types of waves. These characteristics provide insights into the behaviour, propagation, and interactions of waves. Here are some important characteristics of wave motion:

Amplitude ( A ):

The largest deviation a particle can make from its equilibrium location is the amplitude of a wave. It represents the strength or energy of the wave. More energy is transported by the wave with larger amplitudes.

Wavelength ( λ ):

The distance between two consecutive points that are in phase, such as two successive wave crests or troughs, is known as a wave's wavelength. It stands for the length of a single wave cycle.

Frequency ( f ):

The quantity of full oscillations (cycles) that take place within a certain period of time is the frequency of a wave. It is the reciprocal of the wave's period and is expressed in hertz (Hz).

Period ( T ):

The length of time it takes for an oscillation (cycle) to complete determines a wave's period. It is the frequency's reciprocal:

T= 1/ f

Wave Speed ( v ):

The amount of distance a wave covers in a given amount of time is its speed. It is determined by the medium's properties and is related to the wavelength and frequency by v=λ×f

Important Relations

Wave motion is governed by several important relationships and equations that describe the various properties and behaviours of waves. These relationships help us understand and analyse wave phenomena in different contexts. Here are some important relations of wave motion:

• Wave Speed, Frequency, and Wavelength:

The speed ( v ) at which a wave travels is related to its frequency ( f ) and wavelength ( λ ) by the equation:

v= λ ×f

• Period and Frequency:

The period ( T ) of a wave is the reciprocal of its frequency ( f ):

T= 1/ f

• Angular Frequency ( 𝜔 ):

The angular frequency is related to the frequency by 𝜔 =2𝜋 f . It is often used in the analysis of wave phenomena.

• Phase Velocity ( v p ) and Wave Number ( k ):

The phase velocity of a wave ( v _p ) is related to the wave number ( k ) by ​

v _p =𝜔/ k , where ω is the angular frequency.

• Interference:

The displacement at any point caused by the superposition of two or more waves is equal to the sum of the individual displacements, according to the principle of superposition.

• Reflection Angle:

The angle of reflection (θ _r ) is equal to the angle of incidence (θ _i ) when a wave is reflected from a surface, obeying the law of reflection.

• Snell's Law (Refraction):

Snell's Law relates the angles of incidence (θ _i ) and refraction (θ _r ) to the refractive indices ( n 1 and n 2 ) of two media:

n ₁ sin (θ _i ) = n ₂ sin (θ _r )

Doppler Effect:

The Doppler Effect describes the change in frequency ( f ' ) of a wave due to the relative motion between the source and observer. It is given by:

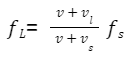
Where,

• f _L is the frequency of sound that the listener perceives (Hz, or 1/s)
• v is the speed of sound in the medium (in m/s)
• v _L is the listener's velocity (m/s)
• v _s is the velocity of the sound source (in m/s)
• f _s is the frequency of sound emitted by the source (Hz, or 1/s)

Intensity ( I ) and Amplitude ( A ):

The intensity of a wave is related to its amplitude ( A ) by:

I α A ²

This indicates that the intensity is proportional to the square of the amplitude.

Polarization:

Polarization of transverse waves is described by the angle (θ ) between the direction of the wave's oscillation and a reference axis. Malus's Law relates the intensities of polarized light before ( I _o ) and after ( I ) passing through a polarizer:

I= I _o cos ² (θ )

These relationships provide fundamental insights into the behaviour of waves, their interactions, and their properties in various contexts, from simple harmonic motion to the behaviour of light and sound waves.

Phase Difference and Path Difference

Phase difference and path difference are important concepts in wave motion, particularly when discussing interference and other wave interactions. They help describe how waves combine or cancel each other out when they meet or overlap.

Phase Difference:

Phase difference refers to the difference in phase (position within their cycle) between two waves at a specific point in time. It is measured in degrees or radians and determines how the wave crests and troughs align or misalign with each other. The phase difference can influence whether waves interfere constructively (reinforce each other) or destructively (cancel each other).

• In-Phase: When two waves have the same frequency and their crests and troughs align perfectly, they are said to be "in-phase" with each other. The phase difference is 0 degrees (or an integer multiple of 360 degrees), and constructive interference occurs.
• Out-of-Phase: When two waves have a phase difference that is not a multiple of 360 degrees, they are "out-of-phase." The crests of one wave may align with the troughs of the other, leading to destructive interference.

Path Difference:

Path difference refers to the difference in the distance travelled by two waves from their sources to a specific point where they interact or overlap. Path difference is crucial in understanding interference patterns, such as those observed in double-slit experiments or in diffraction.

• Constructive Interference: When the path difference is a whole number of wavelengths (e.g., 0λ , 1λ , 2λ ,... ), waves arriving at a point are in phase, leading to constructive interference.
• Destructive Interference: When the path difference is a half-wavelength ( 0.5λ , 1.5λ , 2.5λ ,... ), waves arriving at a point are out of phase, leading to destructive interference.