CBSE Worksheet for chapter- 10 Circle class 10

CBSE Worksheet for chapter- 10 Circle class 10

Worksheet For class 10

Find CBSE Worksheet for chapter- 10 Circle class 10

• CLASS-10
• BOARD: CBSE
• Mathematic Worksheet - 10
• TOPIC: Circle
• For other CBSE Worksheet for class 10 Mathematic check out main page of Physics Wallah.

SUMMARY

• Theorem 1: The perpendicular from the centre of a circle to a chord bisects the chord.
• Theorem 2: There is one and only one circle passing through three given non-collinear points.
• Theorem 3: the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
• Theorem 4: Angles in same segment of a circle are equal.
• Theorem 5: angle in the semicircle is a right angle.
• Theorem 6: the sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
• Theorem 7: Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centers).
• Theorem 8: A tangent to a circle is perpendicular to the radius through the point of contact.
• Theorem 9: Lengths of two tangents drawn from an external point to a circle are equal.

SECTION – I (OBJECTIVE)

1. In a circle of radius 10 cm, the length of chord whose distance is 6 cm from the centre is:

1. 4 cm
2. 5 cm
3. 8 cm
4. 16 cm

2. If a chord of length 8 cm is situated at a distance of 3 cm from centre, then the diameter of circle is:

1. 11cm
2. 10cm
3. 12cm
4. 15cm

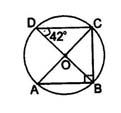
3. In the given circle ABCD, O is the centre and ∠BDC = 42°. Then ∠ACB is equal to:

1. 48°
2. 45°
3. 42°
4. 60°

4.In the given figure, ∠CAB = 80°, ∠ABC = 40°. The sum of ∠DAB + ∠ABD is equal to:

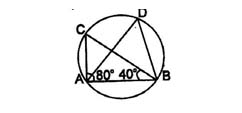
1. 80°
2. 100°
3. 120°
4. 140°

5. In the given figure, if C is the centre of the circle and ∠PQC = 25° and ∠PRC = 15° , then ∠QCR is equal to:

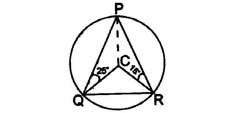
1. 40°
2. 60°
3. 80°
4. 120°

6. In a cyclic quadrilateral if ∠B - ∠D = 60°, then the smaller of the angles B and D is:

1. 30°
2. 45°
3. 60°
4. 75°

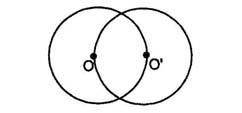
7. In the diagram two equal circles of radius 4 cm intersect each other such that each passes through the centre of the other. Find the length of the common chord.

1. 2 √3 cm
2. 4 √3 cm
3. 4√3 cm
4. 8cm

8. The length of a chord of a circle is equal to the radius of the circle. The angle which this chord subtends on the longer segment of the circle is equal to:

1. 30°
2. 45°
3. 60°
4. 90°

9. The length of the tangent drawn from a point 8 cm away from the centre of a circle of radius 6 cm is:

1. √7 cm
2. 2√7 cm
3. 10 cm
4. 5 cm

10. In a circle radius of 5 cm, AB and AC are two chords such that AB = AC = 6 cm. find the length of the chord BC.

1. 9.6
2. 4.8
3. 10
4. None of these

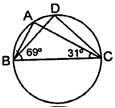
11. In figure, ∠ABC = 69° , ∠ACB = 31° , ∠BDC is:

1. 80°
2. 75°
3. 90°
4. None of these

12.Two parallel chords AB and CD, of lengths 6 cm and 8 cm respectively, are 1 cm apart. The radius of the circle is :

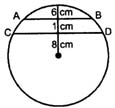
1. 2.5 cm
2. 4 cm
3. 5 cm
4. 5.5 cm

13.In the adjoining figure, x : y is equal to, where O is centre of circle?

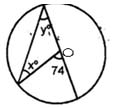
1. 1:1
2. 2:1
3. 3:2
4. 1:4

14.The value of x in the given figure is:

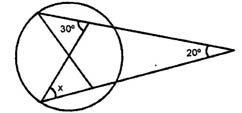
1. 30°
2. 20°
3. 10°
4. 40°