Average Questions for IBPS RRB PO and Clerk Exam

Average in quantitative aptitude is defined as the mean value of a set of numbers or observations. It is calculated by dividing the sum of all the values in the set by the total number of values present. Mathematically, the formula for average.
Average is a fundamental concept in quantitative aptitude representing the central value of a data set, calculated by dividing the sum of all observations by the number of observations. It is a crucial topic for various exams and practical applications.

Ideally, 2 to 3 Average questions are asked in Banking exams, making it an important area to master for scoring well.

Average Questions for IBPS RRB Clerk and PO

Average is an essential arithmetic topic often included under the broader category of Arithmetic Word Problems in the Quantitative Aptitude section.Problems may involve calculating the average of a group, changes in average when a member is added or removed, weighted averages, and related concepts.

Average is part of the Arithmetic segment, which generally contributes about 10-15 questions in the Quantitative Aptitude section of IBPS RRB PO and Clerk prelims and mains exams. Average questions are often combined with Ratio, Percentage, Profit & Loss, Time & Work, and other arithmetic problems in the exam.

Average Formula

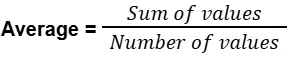
Weightage of Average Questions in Banking Exams

Preliminary Exams:

• Quantitative Aptitude Section: Average problems usually constitute about 2-5% of the total questions in the Quantitative Aptitude section. This means that out of 35-50 questions, around 1-2 questions might be related to Average.

Main Exams:

• Quantitative Aptitude/Mathematics Section: In the main exams, the weightage can be slightly higher. Average problems can make up about 5-10% of the total questions. This could be around 2-5 questions in a section with 50-60 questions.

Average Solved Examples

Problem: Suppose you have the following set of numbers: 5, 8, 12, 20, and 25. To find the average.

Solution:

Sum of the Observations: 5 + 8 + 12 + 20 + 25 = 70

Number of Observations: n = 5

Calculate the Average:

Problem: The average of the first 55 natural numbers is:

Solution: Natural integers = 1, 2, 3,4……………………..55

Sum of 55 natural terms = 1 + 2 + 3 + 4 + ……..+ 55

= (1 + 2 + 3+4……….+ 55)

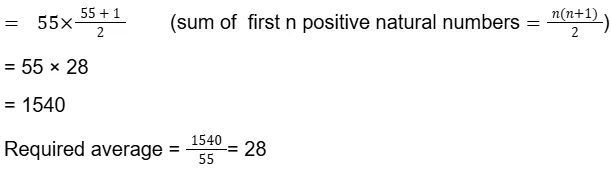
Problem: The average of 13 consecutive numbers is 7. Then find the largest of these numbers?

Solution:

Given, Average of 13 consecutive numbers is 7

So, sum of 13 consecutive numbers = 7 × 13 = 91

Let, the numbers be x, (x+1), (x+2), (x+3), (x+4) ,(x+5) , (x+6), (x+7) , (x+8) , (x+9) , (x+10) , (x+11) , (x+12)

So, x + (x+1) + (x+2) + (x+3) + (x+4) + (x+5) + (x+6) + (x+7) + (x+8) + (x+9) + (x+10) + (x+11) + (x+12)  = 91

=> 13x + 78 = 91

=> 13x = 13

=> x = 1

Thus, largest number = x + 12 = 13

Problem: Find the average of the numbers 12, 15, 18, 22, and 28.

Solution:

Sum of the numbers: 12+15+18+22+28 = 95

Number of observations: 5

Average: 

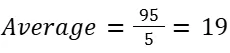
Problem: The average of 5 numbers is 24. If four of the numbers are 18, 25, 22, and 28, find the fifth number.

Solution:

1. Total sum of the 5 numbers: 5 × 24 = 120

2. Sum of the known numbers: 18 + 25 + 22 + 28 = 93

3. Find the fifth number: 120 − 93 = 27

Problem: The average score of Group A (15 students) is 70, and the average score of Group B (10 students) is 85. Find the combined average score.

Solution:

Total score of Group A: 15 × 70 = 1050

Total score of Group B: 10 × 85 = 850

Combined total score: 1050 + 850  =1900

Combined number of students: 15 + 10 = 25

Combined average score: Combined average = 190025 = 76

Problem: A car travels 60 km at 40 km/h and then another 60 km at 60 km/h. Find the average speed of the entire journey.

Solution:

Time taken for the first part of the journey: 6040 = 1.5 hr

Time taken for the second part of the journey: 6060 = 1 hr

Total distance traveled: 60 + 60 = 120 km

Total time taken: 1.5 + 1 = 2.5 hours

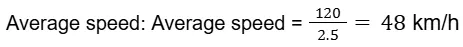
Problem: The average of 4 numbers is 20. The average of another 6 numbers is 30. Find the overall average.

Solution:

Total sum of the first 4 numbers: 4 × 20=80

Total sum of the next 6 numbers: 6 × 30=180

Combined total sum: 80 + 180 = 260

Combined number of observations: 4 + 6 = 10 

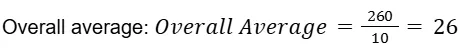
Average Previous Year Asked Questions

Q1. The average age of a group of 5 friends is 28 years. If the age of one friend is 32 years, what is the average age of the remaining 4 friends?

Q2. The average score of 40 students in a class is 65. Another class of 30 students has an average score of 70. What is the average score of all 70 students?

Q3. The average of 6 consecutive numbers is 30. What is the sum of these 6 numbers?

Q4. A student scored 80 in Mathematics, 70 in Science, and 90 in English. If Mathematics and Science have a weightage of 2 each and English has a weightage of 3, find the weighted average score.

Q5. A car travels 150 km at 50 km/h and then 100 km at 80 km/h. What is the average speed for the entire journey?

Q6. The average of 8 numbers is 20. If one of the numbers is 35, find the average of the remaining 7 numbers.

How can I practice Average Questions effectively?

• Solve Previous Year Papers: Review and solve previous year’s banking exam papers to get familiar with the types of average questions asked.

• Use Mock Tests: Practice with mock tests and quizzes that focus on averages and related concepts.

• Understand Key Formulas: Make sure to understand and memorize key formulas related to averages, weighted averages, and average speed.

Banking Exam Online Course – Join Today!!