Physics Wallah

Quadratic Equation, Definition, Formula, Examples Tricks To Solve Quadratic Equation

Quadratic equations are discussed here. A quadratic equation is a quadratic polynomial equation, meaning that at least one squared term is an element in the equation. Candidates can learn about Meaning, examples, and tips to solve quadratic equations.
authorImagePriyanka Dahima8 Oct, 2025
Share

Share

Quadratic Equation

Key Concepts for Quadratic Equation: A quadratic polynomial, when equated to zero, becomes a quadratic equation. In other terms, a quadratic equation is a second-degree algebraic equation. The values of x satisfying the equation are called the roots of the quadratic equation.

General form: a x 2 +bx+c=0 where x represents an unknown, and a, b, and c are constants with a not equal to 0  . The constants a, b, and c are usually real numbers, but they can be complex numbers as well. Quadratic equation examples: x 2 +5x+6=0 , 6 x 2 -17x+12=0

Quadratic Equation Formula

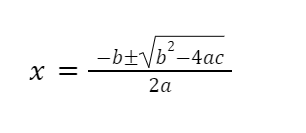The Quadratic Equation Formula expresses the solutions in terms of a , b , and c .

Best Quadratic Equation Examples

In each question, two equations will be given. You have to solve the equations and choose the appropriate relation between “x” and “y” and choose the appropriate relation between “x” and “y” from the options and choose the correct option.
  1. a) x<y
  2. b) x>y
  3. c) xy
  4. d) xy
  5. e) x= y or the relation can not be established

1)  I. x2-9x+20=0  II. y2-7y+12=0

Solution:

I. x 2 -9x+20=0 x 2 -4x-5x+20=0 x(x-4)-5(x-4)=0

x=4,5

II. y 2 -7y+12=0 y 2 -4y-3y+12=0 y(y-4)-3(y-4)=0

y=4,3

Case 1: x = 4, x = 4  (x = y)

Case 2: x = 4, x = 3  (x > y)

Case 3: x = 5, x = 4  (x > y)

Case 4: x = 5, x = 3  (x > y)

So, x y

2)  I. x2-5x-14=0   II. y2-16y+64=0

Solution:

  1. x 2 -5x-14=0
x 2 -7x+2x-14=0 x(x-7)+2(x-7)=0

x=7,-2

  1. y 2 -16y+64=0
y 2 -8y-8y+64=0 y(y-8)-8(y-8)=0

y=8,8

Case 1: x = 7, y = 8  (y > x) Case 2: x = 7, y = 8  (y > x) Case 3: x = -2, y = 8 (y > x) Case 4: x = -2, y = 8 (y > x) So, x<y

3)  I.  x2 + 7x+12=0    II. y2+9y+20=0

Solution:

I . x 2 + 7x+12=0 x 2 +4x+3x +12=0 x(x + 4)+3(x+4) = 0 (x +4) (x +3)=0 x = -3, -4
  1. y 2 +9y+20=0
y 2 + 5y+4y+20=0 y(y + 5)+4 y+5 =0 y = -5, -4 Case 1: x = -3, y = -5  (x > y) Case 2: x = -4, y = -5  (x > y) Case 3: x = -3, y = -4  (x > y) Case 4: x =-4, y = -4  (x = y) So, x y

Tricks to Solve Quadratic Equations Questions:

Solving quadratic equations tips and tricks are given in this section.

Trick 1: Quadratic equations  solution based on the sign of coefficients in the equation: 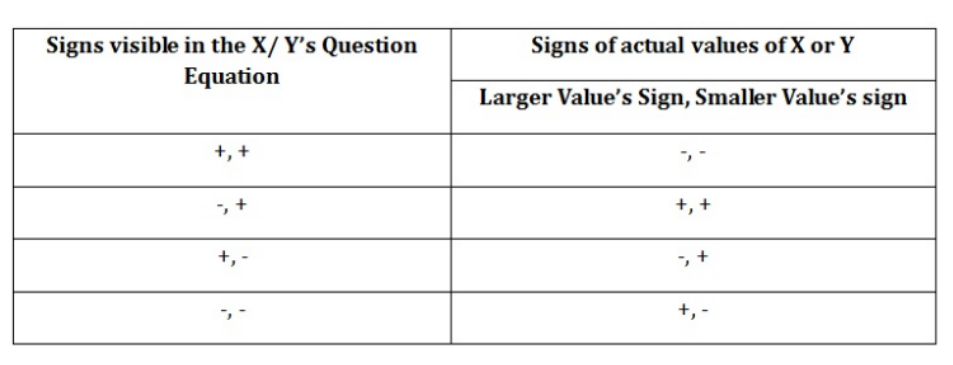For example:

  1. x 2 -14x+45=0
  2. y 2 +7y+6=0

In this example, the signs visible in the x equation are ( -, +) and signs visible in the y equation are (+, +). So, signs of actual value of x and y in the final answer will be ( +, +) and ( -, -) So, “ Relationships can’t be established”.

 

Trick 2:  Constant term negative in both equations = Relationship can’t be established. Practice problems:
  1. 2 x 2 -11x-15=0
  2. 21 y 2 +23y-6=0
In this example, the constant term is negative in both equations. So, the correct answer is “ Relationships can’t be established”.

Weightage of Quadratic Equations in Banking Exams:

 The weightage of quadratic equations can vary from one exam to another and even within different sections of the same exam. It's challenging to provide an exact weightage for Application of quadratic equation, they are usually part of a broader set of topics in the quantitative aptitude section, which also includes topics like arithmetic, geometry, number systems, data interpretation, and so on. As such, candidates preparing for banking exams should ensure they have a solid understanding of quadratic equations and practice solving various types of problems to maximize their chances of success. Roughly weightage - (0-5) Questions Solved Problems: 1) I. x 2 - 14x+45= 0
  1. y 2 -18y+72=0
  2. a) x<y
  3. b) x>y
  4. c) x y
  5. d) x y
  6. e) x= y or the relation can not be established

Solution:

I . x 2 - 14x+45= 0 x 2 - 9x-5x+45= 0 x(x -9)-5(x-9)=0 x = 9, 5
  1. y 2 -18y+72=0
y 2 – 12y-6y+72=0 y(y – 12) -6 y-12 =0 y = 12, 6 Case 1: x = 9, y = 12 (y > x) Case 2: x = 9 , y = 6 (x > y) Case 3: x = 5, y = 12 (y > x) Case 4: x = 5, y = 6 (y > x) no relation can be established between x and y.

2) I. x2 + 32x + 240 = 0

  1. y 2 + 3y – 108 = 0
  2. A)  x > y
  3. B) x < y
  4. C) x = y or the relationship cannot be established
  5. D) x ≥ y
  6. E) x ≤ y

Solution:

From I: x 2 + 32x + 240 = 0 x 2 + 20x + 12x + 240 = 0 x(x + 20) + 12(x + 20) = 0 (x + 20)(x + 12) = 0 x = -20, -12 From II: y 2 + 3y – 108 = 0 y 2 + 12y – 9y – 108 = 0 y(y + 12) – 9(y + 19) = 0 (y + 12)(y – 9) = 0 y = -12, 9 Case 1: x = -20, y = -12 ( y > x) Case 2: x = -20, y = 9  (y > x) Case 3: x = -12, y = -12  ( x = y ) Case 4: x = -20, y = 9  (y > x) So, y ≥ x

3) I. 6x² + 19x + 15 = 0

  1. 24y² + 11y + 1 = 0
  2. a) if x > y
  3. b) if x ≥ y
  4. c) if x < y
  5. d) if x ≤ y
  6. e) if x = y or the relationship cannot be established.

Solution:

  1. 6x² + 19x + 15 = 0
⇒ 6x² + 9x + 10x + 15 = 0 ⇒ (2x + 3) (3x + 5) = 0 ⇒ x = –3/2, –5/3
  1. 24y² + 11y + 1 = 0
⇒ 24y² + 8y + 3y + 1= 0 ⇒ (3y + 1) (8y + 1) = 0 ⇒ y = –1/3, –1/8 Case 1: x = -3/2, y = -⅓   (y > x) Case 2: x = -3/2, y = -⅛   (y > x) Case 3: x = -5/3, y = -⅓  (y > x) Case 4: x = -5/3, y = -⅛  (y > x) So, y > x

4) I. 2x2- x - 1=0

  1. 2y 2 - 4y +2=0
  2. a) if x > y
  3. b) if x ≥ y
  4. c) if x < y
  5. d) if x ≤ y
  6. e) if x = y or the relationship cannot be established.

Solution:

From equation I 2x 2 -x-1=0 2 x 2 -2x+x-1=0 2x(x-1) +1(x-1)=0 (2x+1) (x-1)=0 x= -1 2 , 1 From equation II 2y 2 - 4y +2=0 2y 2 - 2y - 2y +2=0 2y(y-1)- 2(y-1)=0 (2y-2) (y-1)=0 y = 1, 1 Case 1: x = -½, y = 1 (y>x) Case 2: x = -½, y = 1 (y>x) Case 3: x = 1, y = 1 (y=x) Case 4: x = 1, y = 1 (y=x) So, x ≤ y

5)  I . 4x2- 7x - 57 =0

II. 5y 2 - 6y - 63=0
  1. a) if x > y
  2. b) if x ≥ y
  3. c) if x < y
d)if x = y or the relationship cannot be established.
  1. e)  if x ≤ y

Solution:

From equation I 4x 2 -7x - 57 =0 4x 2 -19x+12x-57 =0 x(4x-19) +3(4x-19) =0 (4x-19) (x+3) =0 x= 19 4 ,-3 From equation II 5y 2 - 6y - 63=0 5y 2 -21y+15y-63 =0 y(5y-21) +3(5y-21) =0 (y+3)(5y-21)=0 y = -3, 21 5 Case 1: x = 19 4 , y = -3 (x > y) Case 2: x = 19 4 , y = 21 5 (x > y) Case 3: x = -3, y = -3 (x = y) Case 4: x = -3, y = 21 5 (y > x) So, x = y or relationship between x and y can't be established.

Previous Year Questions Of Quadratic Equations Asked In Banking Exams :

1) I. 5 x 2 +3x-14=0 II. 5 y 2 +3y-2=0 2) I. x 2 +9x+20=0 II. 7 y 2 -19y+10=0 3) I. x 2 -7x+10=0 II. y 2 -5y+6=0 4)  I. x 2 +12x+35=0 II. 3 y 2 +19y+20=0 5) I. x 2 -3x-88=0 II. y 2 +8y-48=0 6) I. 4 x 2 -13x+10=0 II. 2 y 2 -15y+28=0 7) I. 2 x 2 +15x+27=0 II. 3 y 2 +25y-18=0 8) I. 6 x 2 -5x+1=0 II. 15 y 2 -8y+1=0 9) I. 7 x 2 -23x+18=0 II. 4 y 2 -9y+5= 10) I. 10 x 2 -11x-6=0 II. y 2 +5y+6=0

Related Links
Quadratic Equations Number System
Vedic Maths Pie Chart DI
Time and Work Problem on Ages
Flow Chart DI
Arithmetic DI Permutation and Combination

Quadratic Equation FAQs

Q1. What are the different ways to solve a quadratic equation?

Ans. Sometimes, solving quadratic equations can  be quite difficult . However, various methods exist, depending on the nature of the quadratic equation. Four primary approaches are commonly employed: factoring, utilizing square roots, completing the square, and employing the quadratic formula.

Q2. What are the steps involved in factoring a quadratic equation?

Ans. To solve a quadratic equation using the factoring method, follow these steps: Begin by consolidating all terms on one side of the equation, leaving zero on the opposite side, then proceed to factorize. Next, set each factor equal to zero and solve each resulting equation individually. Verify the solutions by substituting them back into the original equation.

Q3. What is the standard form of the quadratic equation?

Ans.  The form ax2+bx+c=0 is said to be the standard form of a quadratic equation.

Q4. What is the golden rule of the quadratic equation?

The solution to the quadratic equation x2-x-1=0 is the golden ratio, an irrational number. For example, ϕ = 1 + 5 2 = 1.618033988 is the golden ratio. The words "divine section," "medial section," "golden cut," "extreme and mean ratio," and others are also used to describe the golden ratio.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
07290070560
Check out these Related Articles
BlogImage
BANKING
Share
LIC AAO Mains 2025 Revised Reporting Timings Announced
Read Full Story
6 Nov 2025, 05:18 pm
BlogImage
BANKING
Share
NICL AO Phase 2 Result 2025 Out, Download Mains Result PDF
Read Full Story
6 Nov 2025, 02:57 pm
BlogImage
BANKING
Share
Alphabetical Series for Bank Exams: Tricks, Solved Qs & Concepts
Read Full Story
6 Nov 2025, 03:23 pm
BlogImage
BANKING
Share
South Indian Bank Eligibility Criteria 2025: Age Limit, Education, Nationality
Read Full Story
31 Oct 2025, 02:57 pm
BlogImage
BANKING
Share
South Indian Bank Selection Process 2025 for Junior Officer / Business Promotion Officer Posts
Read Full Story
4 Nov 2025, 03:05 pm
BlogImage
BANKING
Share
IBPS Clerk Exam Shift Timings 2025 for Mains Exam
Read Full Story
4 Nov 2025, 02:02 pm
BlogImage
BANKING
Share
SIDBI Grade A, B Result 2025 Phase 2 (Out), Download Merit List PDF
Read Full Story
5 Nov 2025, 12:38 pm
BlogImage
RBI
Share
LIC AAO Mains Exam Date 2025 (Out), Check Mains Exam Date and Schedule
Read Full Story
5 Nov 2025, 04:52 pm
BlogImage
SBI
Share
SBI Clerk Prelims Result 2025 Out, Here’s What Past 3 Years’ Trends Say
Read Full Story
5 Nov 2025, 04:26 pm
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App