Angle Between Two Lines Formula, Calculate, Application

The concept of angles is fundamental in mathematics and plays a crucial role in various fields, from geometry to physics and engineering. One particular application that frequently arises is finding the angle between two lines in a two-dimensional plane. This seemingly straightforward task involves trigonometric principles and can be a valuable tool in solving a wide range of problems. In this comprehensive guide, we will explore the theory behind finding the angle between two lines, provide step-by-step instructions on how to calculate it and delve into practical applications in different domains.

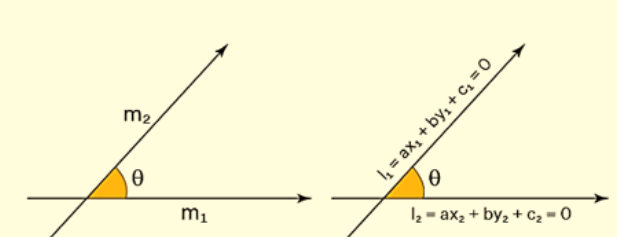
The angle between two lines represents the degree of inclination between them. When two lines intersect, they create two types of angles: the acute angle and the obtuse angle. In this context, we are primarily interested in the acute angle formed between the lines.

To calculate the angle between two lines with slopes denoted as m1 and m2, you can use the following formula:

= tan -1 |(m 1 - m 2 )/(1 + m 1 m 2 )|

Now, let's explore all the relevant formulas associated with finding the angle between two lines, both in a two-dimensional coordinate plane and in three-dimensional space, to provide a comprehensive understanding of this geometric concept.

How to Find Angle Between Two Lines?

You can determine the angle between two lines either by having information about their slopes or by knowing their equations. Typically, when finding the angle between two lines, we're interested in the acute angle formed between them.

To calculate this acute angle, given two lines with slopes represented as m1 and m2, you can use the trigonometric tangent function. The formula for calculating the acute angle between the two lines is as follows:

Additionally, you can determine the angle between two lines when their equations are provided. Suppose the equations of the two lines are given as:

The angle between the two lines can be computed by the tangent of the angle between the two lines.

Formulas for Angle Between Two Lines

The formulas for easily calculating the angle between two lines:

Angle Between a Line and the X-Axis:

The angle between two lines, of which, one of the line is ax + by + c = 0, and the other line is the x-axis, is θ = tan -1 (-a/b).

The angle between two lines, of which one of the line is y=mx+c and the other line is the x-axis, is θ = tan -1 m.

The angle between two lines that are parallel to each other and have equal slopes

The angle between two lines which are perpendicular to each other and have the product of their slopes equal to -1 is 90º.

Also Check – Introduction to Graph Formula

Angle Between Two Lines In Three Dimensional Space

Calculating the angle between two lines in three-dimensional space follows a similar principle to finding the angle between lines in a two-dimensional coordinate plane. When you have two lines represented by equations:

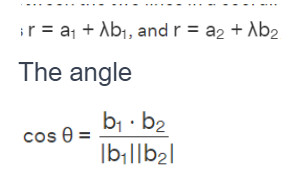
θ between these lines can be determined using the following formula:

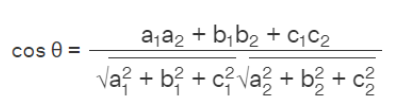
Now that we have a clear understanding of how to calculate the angle between two lines, let's explore some practical applications across different fields.

Also Check – Ratio and Proportion Formula

Application of Angle Between Two Lines Formula

1 Engineering and Construction

In civil engineering and construction, knowing the angle between intersecting lines is crucial for designing structures, roads, and pipelines. For example, when designing a bridge, engineers need to determine the angle between the banks of a river to ensure the bridge is constructed at the correct angle for safe and efficient crossing.

2 Astronomy

In astronomy, astronomers often need to calculate angles between celestial objects, such as stars or planets, and reference lines. This information helps astronomers make observations, track the movement of celestial bodies, and predict celestial events like eclipses.

3 Navigation

In navigation, especially in aviation and maritime contexts, finding the angle between the path of a vehicle and a reference line (e.g., the horizon or a specific compass direction) is essential for determining the vehicle's heading. This information is vital for safe and accurate navigation.

4 Computer Graphics and Game Development

In computer graphics and game development, understanding the angle between two vectors is crucial for various applications, including character movement, camera rotation, and collision detection. Game developers use trigonometric principles to calculate angles and ensure realistic interactions within virtual environments.

5 Physics

In physics, angles between vectors are often used to describe the direction of forces, velocities, and accelerations. These angles play a pivotal role in mechanics, electromagnetism, and other branches of physics.

6 Geophysics

In geophysics, the angle between seismic waves and the direction of measurement is crucial for interpreting seismic data and understanding subsurface geological structures. Accurate angle calculations are essential for mapping the Earth's interior.

Conclusion

In conclusion, understanding how to calculate the angle between two lines is a valuable skill with applications in various fields, from engineering and astronomy to navigation and computer graphics. The formula involving slopes and trigonometric functions provides a systematic approach to finding this angle accurately.

Whether you're designing structures, navigating the skies, or developing video games, the ability to calculate angles between lines is a fundamental tool that can enhance your problem-solving capabilities and contribute to more precise and informed decision-making.