

NCERT Solutions for Class 12 Maths Chapter 11
NCERT Solutions for Class 12 Maths Chapter 11: The Three Dimensional Geometry Class 12 solutions in this article help students understand the subject better. The article is a great reference tool and it makes understanding Three Dimensional Geometry less of a challenge for students. Everything around us appears as three-dimensional. In this article, the Physics Wallah experts have explained what Three Dimensional Geometry is all about in details. Diligent practicing of the solutions given here is sure to help students score well in the board exams. The Maths Class 12 Chapter 11 Three Dimensional Geometry solutions in this article have been given in very simple steps making them easy to understand for students. The solutions include every step in details making things easy for even the weaker students. It helps them greatly to clearly understand Three Dimensional Geometry Class 12 removing all confusion. The solutions given here follow the CBSE Syllabus for 2023-24. Our experts have tried to see things through the eyes of students and that has helped keep the explanations very simple. Students can download the PDF file for free and refer to it every time they study.NCERT Solutions for Class 12 Maths Chapter 11 Overview
This article from Physics Wallah intends to remove the doubts students have about Three Dimensional Geometry Class 12 . The solutions have been given keeping the difficulties faced by the weaker students in mind. As such, they are easy to understand. Not a single step has been skipped in the solutions and that’s sure to help students grasp NCERT Solutions for Class 12 Maths Chapter 11 very well. The Class 12 Maths Chapter 11 Three Dimensional Geometry solutions given here help students find clarity in their concepts of the subject. Regular practice while using this article for reference is sure to help students sharpen their skills in Three Dimensional Geometry. Care has been taken to see to it that students are left with no confusion at the end of the article by including detailed explanations.NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry
Exercise 11.1 Page No. 467 1. If a line makes angles 90°, 135°, 45° with the x, y and z-axes, respectively, find its direction cosines. Solution: Let the direction cosines of the line be l, m and n. Here let α = 90°, β = 135° and γ = 45° So, l = cos α, m = cos β and n = cos γ So, the direction cosines are l = cos 90° = 0 m = cos 135°= cos (180° – 45°) = -cos 45° = -1/ √ 2 n = cos 45° = 1/ √ 2 ∴ The direction cosines of the line are 0, -1/ √ 2, 1/ √ 2 2. Find the direction cosines of a line which makes equal angles with the coordinate axes. Solution: Given: Angles are equal. So, let the angles be α, β, γ Let the direction cosines of the line be l, m and n. l = cos α, m = cos β and n = cos γ Here, given α = β = γ (Since, line makes equal angles with the coordinate axes) … (1) The direction cosines are l = cos α, m = cos β and n = cos γ We have, l 2 + m 2 + n 2 = 1 cos 2 α + cos 2 β + cos 2 γ = 1 From (1) we have, cos 2 α + cos 2 α + cos 2 α = 1 3 cos 2 α = 1 Cos α = ± √( 1/3) ∴ The direction cosines are l = ± √( 1/3), m = ± √( 1/3), n = ± √( 1/3) 3. If a line has the direction ratios –18, 12, –4, then what are its direction cosines? Solution: Given: Direction ratios as -18, 12, -4 Where, a = -18, b = 12, c = -4 Let us consider the direction ratios of the line as a, b and c Then the direction cosines are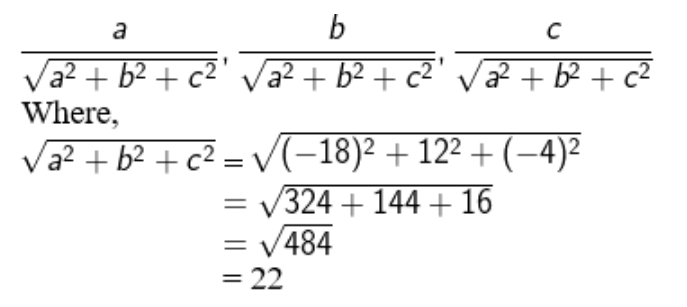 ∴ The direction cosines are
-18/22, 12/22, -4/22 => -9/11, 6/11, -2/11
4. Show that the points (2, 3, 4), (–1, –2, 1), (5, 8, 7) are collinear.
Solution:
If the direction ratios of two lines segments are proportional, then the lines are collinear.
Given:
A(2, 3, 4), B(−1, −2, 1), C(5, 8, 7)
Direction ratio of line joining A (2, 3, 4) and B (−1, −2, 1), are
(−1−2), (−2−3), (1−4) = (−3, −5, −3)
Where, a
1
= -3, b
1
= -5, c
1
= -3
Direction ratio of line joining B (−1, −2, 1) and C (5, 8, 7) are
(5− (−1)), (8− (−2)), (7−1) = (6, 10, 6)
Where, a
2
= 6, b
2
= 10 and c
2
=6
Now,
∴ The direction cosines are
-18/22, 12/22, -4/22 => -9/11, 6/11, -2/11
4. Show that the points (2, 3, 4), (–1, –2, 1), (5, 8, 7) are collinear.
Solution:
If the direction ratios of two lines segments are proportional, then the lines are collinear.
Given:
A(2, 3, 4), B(−1, −2, 1), C(5, 8, 7)
Direction ratio of line joining A (2, 3, 4) and B (−1, −2, 1), are
(−1−2), (−2−3), (1−4) = (−3, −5, −3)
Where, a
1
= -3, b
1
= -5, c
1
= -3
Direction ratio of line joining B (−1, −2, 1) and C (5, 8, 7) are
(5− (−1)), (8− (−2)), (7−1) = (6, 10, 6)
Where, a
2
= 6, b
2
= 10 and c
2
=6
Now,
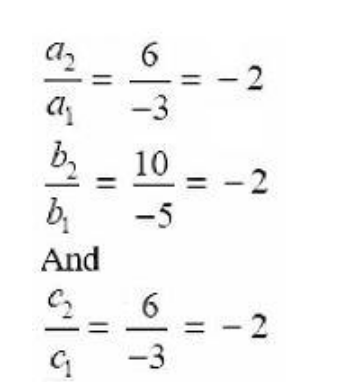 ∴ A, B, C are collinear.
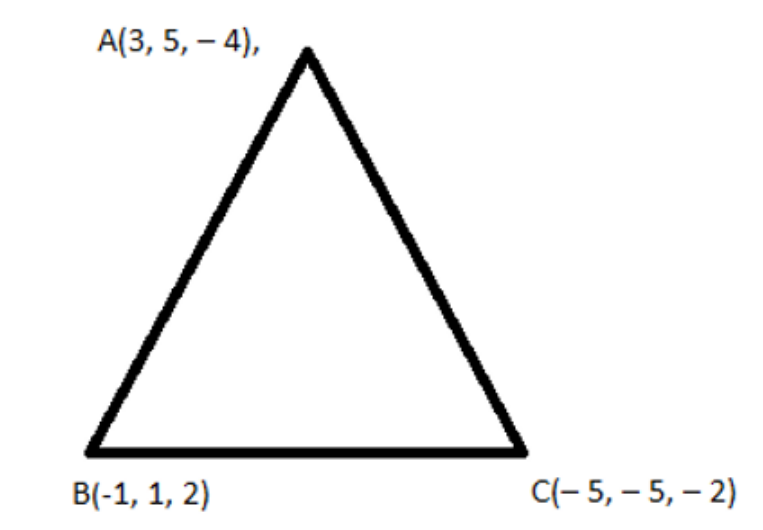
5. Find the direction cosines of the sides of the triangle whose vertices are (3, 5, –4), (-1, 1, 2) and (–5, –5, –2).
Solution:
Given:
The vertices are (3, 5, –4), (-1, 1, 2) and (–5, –5, –2).
∴ A, B, C are collinear.
5. Find the direction cosines of the sides of the triangle whose vertices are (3, 5, –4), (-1, 1, 2) and (–5, –5, –2).
Solution:
Given:
The vertices are (3, 5, –4), (-1, 1, 2) and (–5, –5, –2).
 The direction cosines of the two points passing through A(x
1
, y
1
, z
1
) and B(x
2
, y
2
, z
2
) is given by (x
2
– x
1
), (y
2
-y
1
), (z
2
-z
1
)
Firstly let us find the direction ratios of AB
Where, A = (3, 5, -4) and B = (-1, 1, 2)
Ratio of AB = [(x
2
– x
1
)
2
, (y
2
– y
1
)
2
, (z
2
– z
1
)
2
]
= (-1-3), (1-5), (2-(-4)) = -4, -4, 6
Then by using the formula,
√[(x
2
– x
1
)
2
+ (y
2
– y
1
)
2
+ (z
2
– z
1
)
2
]
√[(-4)
2
+ (-4)
2
+ (6)
2
] = √(16+16+36)
= √68
= 2√17
Now let us find the direction cosines of the line AB
By using the formula,
The direction cosines of the two points passing through A(x
1
, y
1
, z
1
) and B(x
2
, y
2
, z
2
) is given by (x
2
– x
1
), (y
2
-y
1
), (z
2
-z
1
)
Firstly let us find the direction ratios of AB
Where, A = (3, 5, -4) and B = (-1, 1, 2)
Ratio of AB = [(x
2
– x
1
)
2
, (y
2
– y
1
)
2
, (z
2
– z
1
)
2
]
= (-1-3), (1-5), (2-(-4)) = -4, -4, 6
Then by using the formula,
√[(x
2
– x
1
)
2
+ (y
2
– y
1
)
2
+ (z
2
– z
1
)
2
]
√[(-4)
2
+ (-4)
2
+ (6)
2
] = √(16+16+36)
= √68
= 2√17
Now let us find the direction cosines of the line AB
By using the formula,
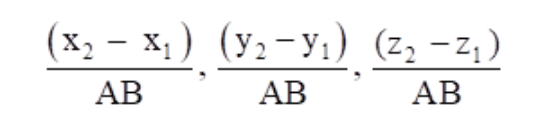 -4/2√17 , -4/2√17, 6/2√17
Or -2/√17, -2/√17, 3/√17
Similarly,
Let us find the direction ratios of BC
Where, B = (-1, 1, 2) and C = (-5, -5, -2)
Ratio of AB = [(x
2
– x
1
)
2
, (y
2
– y
1
)
2
, (z
2
– z
1
)
2
]
= (-5+1), (-5-1), (-2-2) = -4, -6, -4
Then by using the formula,
√[(x
2
– x
1
)
2
+ (y
2
– y
1
)
2
+ (z
2
– z
1
)
2
]
√[(-4)
2
+ (-6)
2
+ (-4)
2
] = √(16+36+16)
= √68
= 2√17
Now, let us find the direction cosines of the line AB
By using the formula,
-4/2√17 , -4/2√17, 6/2√17
Or -2/√17, -2/√17, 3/√17
Similarly,
Let us find the direction ratios of BC
Where, B = (-1, 1, 2) and C = (-5, -5, -2)
Ratio of AB = [(x
2
– x
1
)
2
, (y
2
– y
1
)
2
, (z
2
– z
1
)
2
]
= (-5+1), (-5-1), (-2-2) = -4, -6, -4
Then by using the formula,
√[(x
2
– x
1
)
2
+ (y
2
– y
1
)
2
+ (z
2
– z
1
)
2
]
√[(-4)
2
+ (-6)
2
+ (-4)
2
] = √(16+36+16)
= √68
= 2√17
Now, let us find the direction cosines of the line AB
By using the formula,
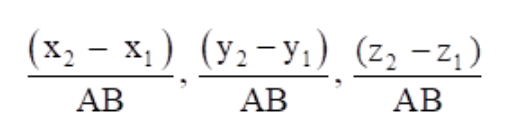 -4/2√17, -6/2√17, -4/2√17
Or -2/√17, -3/√17, -2/√17
Similarly,
Let us find the direction ratios of CA
Where, C = (-5, -5, -2) and A = (3, 5, -4)
Ratio of AB = [(x
2
– x
1
)
2
, (y
2
– y
1
)
2
, (z
2
– z
1
)
2
]
= (3+5), (5+5), (-4+2) = 8, 10, -2
Then, by using the formula,
√[(x
2
– x
1
)
2
+ (y
2
– y
1
)
2
+ (z
2
– z
1
)
2
]
√[(8)
2
+ (10)
2
+ (-2)
2
] = √(64+100+4)
= √168
= 2√42
Now, let us find the direction cosines of the line AB
By using the formula,
-4/2√17, -6/2√17, -4/2√17
Or -2/√17, -3/√17, -2/√17
Similarly,
Let us find the direction ratios of CA
Where, C = (-5, -5, -2) and A = (3, 5, -4)
Ratio of AB = [(x
2
– x
1
)
2
, (y
2
– y
1
)
2
, (z
2
– z
1
)
2
]
= (3+5), (5+5), (-4+2) = 8, 10, -2
Then, by using the formula,
√[(x
2
– x
1
)
2
+ (y
2
– y
1
)
2
+ (z
2
– z
1
)
2
]
√[(8)
2
+ (10)
2
+ (-2)
2
] = √(64+100+4)
= √168
= 2√42
Now, let us find the direction cosines of the line AB
By using the formula,
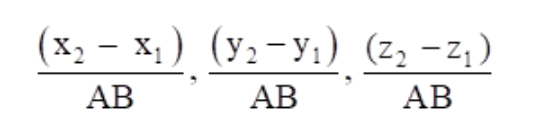 8/2√42, 10/2√42, -2/2√42
Or 4/√42, 5/√42, -1/√42
8/2√42, 10/2√42, -2/2√42
Or 4/√42, 5/√42, -1/√42
EXERCISE 11.2 PAGE NO: 477
1. Show that the three lines with direction cosines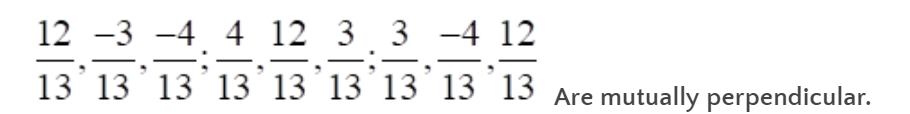 Solution:
Let us consider the direction cosines of L
1
, L
2
and L
3
be l
1
, m
1
, n
1
; l
2
, m
2
, n
2
and l
3
, m
3
, n
3
.
We know that
If l
1
, m
1
, n
1
and l
2
, m
2
, n
2
are the direction cosines of two lines,
And θ is the acute angle between the two lines,
Then cos θ = |l
1
l
2
+ m
1
m
2
+ n
1
n
2
|
If two lines are perpendicular, then the angle between the two is θ = 90°
For perpendicular lines, | l
1
l
2
+ m
1
m
2
+ n
1
n
2
| = cos 90° = 0, i.e. | l
1
l
2
+ m
1
m
2
+ n
1
n
2
| = 0
So, in order to check if the three lines are mutually perpendicular, we compute | l
1
l
2
+ m
1
m
2
+ n
1
n
2
| for all the pairs of the three lines.
Firstly let us compute, | l
1
l
2
+ m
1
m
2
+ n
1
n
2
|
Solution:
Let us consider the direction cosines of L
1
, L
2
and L
3
be l
1
, m
1
, n
1
; l
2
, m
2
, n
2
and l
3
, m
3
, n
3
.
We know that
If l
1
, m
1
, n
1
and l
2
, m
2
, n
2
are the direction cosines of two lines,
And θ is the acute angle between the two lines,
Then cos θ = |l
1
l
2
+ m
1
m
2
+ n
1
n
2
|
If two lines are perpendicular, then the angle between the two is θ = 90°
For perpendicular lines, | l
1
l
2
+ m
1
m
2
+ n
1
n
2
| = cos 90° = 0, i.e. | l
1
l
2
+ m
1
m
2
+ n
1
n
2
| = 0
So, in order to check if the three lines are mutually perpendicular, we compute | l
1
l
2
+ m
1
m
2
+ n
1
n
2
| for all the pairs of the three lines.
Firstly let us compute, | l
1
l
2
+ m
1
m
2
+ n
1
n
2
|
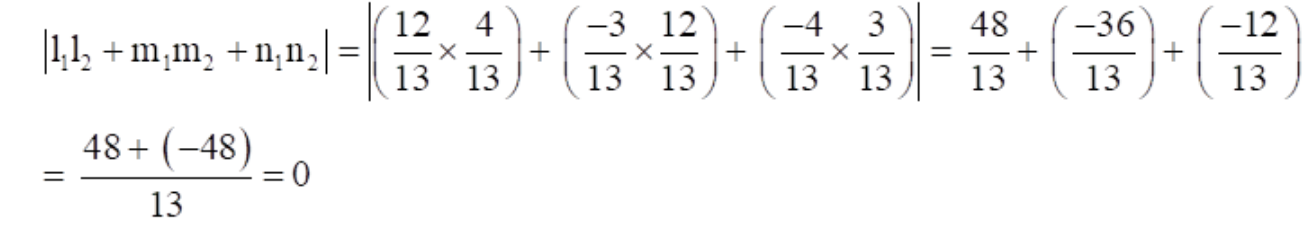 So, L
1
⊥
L
2
…… (1)
Similarly,
Let us compute, | l
2
l
3
+ m
2
m
3
+ n
2
n
3
|
So, L
1
⊥
L
2
…… (1)
Similarly,
Let us compute, | l
2
l
3
+ m
2
m
3
+ n
2
n
3
|
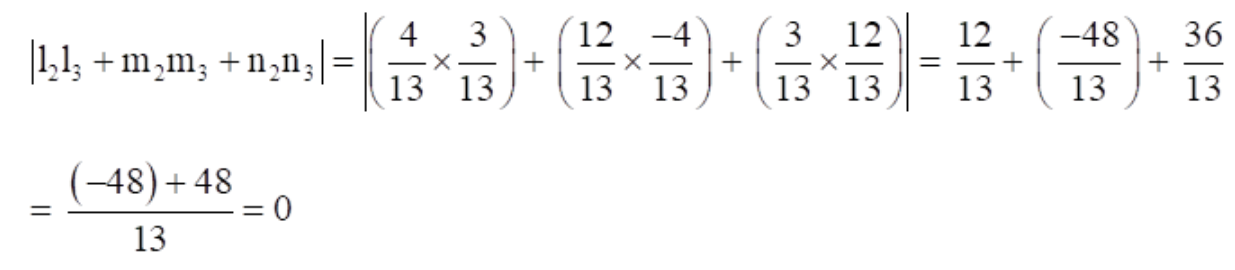 So, L
2
⊥
L
3
….. (2)
Similarly,
Let us compute, | l
3
l
1
+ m
3
m
1
+ n
3
n
1
|
So, L
2
⊥
L
3
….. (2)
Similarly,
Let us compute, | l
3
l
1
+ m
3
m
1
+ n
3
n
1
|
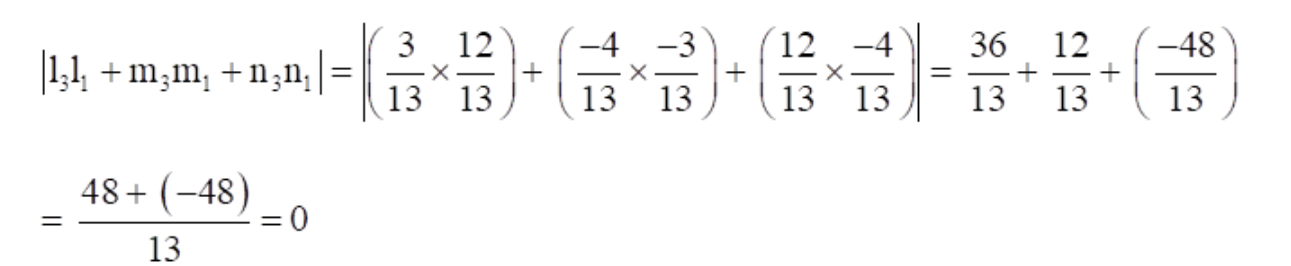 So, L
1
⊥
L
3
….. (3)
∴ By (1), (2) and (3), the lines are perpendicular.
L
1
, L
2
and L
3
are mutually perpendicular.
2. Show that the line through the points (1, –1, 2), (3, 4, –2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Solution:
Given:
The points (1, –1, 2), (3, 4, –2) and (0, 3, 2), (3, 5, 6).
Let us consider AB be the line joining the points, (1, -1, 2) and (3, 4, -2), and CD be the line through the points (0, 3, 2) and (3, 5, 6).
Now,
The direction ratios, a
1
, b
1
, c
1
of AB are
(3 – 1), (4 – (-1)), (-2 – 2) = 2, 5, -4.
Similarly,
The direction ratios, a
2
, b
2
, c
2
of CD are
(3 – 0), (5 – 3), (6 – 2) = 3, 2, 4.
Then, AB and CD will be perpendicular to each other, if a
1
a
2
+ b
1
b
2
+ c
1
c
2
= 0
a
1
a
2
+ b
1
b
2
+ c
1
c
2
= 2(3) + 5(2) + 4(-4)
= 6 + 10 – 16
= 0
∴ AB and CD are perpendicular to each other.
3. Show that the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (–1, –2, 1), (1, 2, 5).
Solution:
Given:
The points (4, 7, 8), (2, 3, 4) and (–1, –2, 1), (1, 2, 5).
Let us consider AB to be the line joining the points, (4, 7, 8), (2, 3, 4) and CD to be the line through the points (–1, –2, 1), (1, 2, 5).
Now,
The direction ratios, a
1
, b
1
, c
1
of AB are
(2 – 4), (3 – 7), (4 – 8) = -2, -4, -4.
The direction ratios, a
2
, b
2
, c
2
of CD are
(1 – (-1)), (2 – (-2)), (5 – 1) = 2, 4, 4.
Then, AB will be parallel to CD, if
So, L
1
⊥
L
3
….. (3)
∴ By (1), (2) and (3), the lines are perpendicular.
L
1
, L
2
and L
3
are mutually perpendicular.
2. Show that the line through the points (1, –1, 2), (3, 4, –2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Solution:
Given:
The points (1, –1, 2), (3, 4, –2) and (0, 3, 2), (3, 5, 6).
Let us consider AB be the line joining the points, (1, -1, 2) and (3, 4, -2), and CD be the line through the points (0, 3, 2) and (3, 5, 6).
Now,
The direction ratios, a
1
, b
1
, c
1
of AB are
(3 – 1), (4 – (-1)), (-2 – 2) = 2, 5, -4.
Similarly,
The direction ratios, a
2
, b
2
, c
2
of CD are
(3 – 0), (5 – 3), (6 – 2) = 3, 2, 4.
Then, AB and CD will be perpendicular to each other, if a
1
a
2
+ b
1
b
2
+ c
1
c
2
= 0
a
1
a
2
+ b
1
b
2
+ c
1
c
2
= 2(3) + 5(2) + 4(-4)
= 6 + 10 – 16
= 0
∴ AB and CD are perpendicular to each other.
3. Show that the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (–1, –2, 1), (1, 2, 5).
Solution:
Given:
The points (4, 7, 8), (2, 3, 4) and (–1, –2, 1), (1, 2, 5).
Let us consider AB to be the line joining the points, (4, 7, 8), (2, 3, 4) and CD to be the line through the points (–1, –2, 1), (1, 2, 5).
Now,
The direction ratios, a
1
, b
1
, c
1
of AB are
(2 – 4), (3 – 7), (4 – 8) = -2, -4, -4.
The direction ratios, a
2
, b
2
, c
2
of CD are
(1 – (-1)), (2 – (-2)), (5 – 1) = 2, 4, 4.
Then, AB will be parallel to CD, if
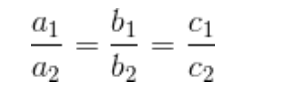 So, a
1
/a
2
= -2/2 = -1
b
1
/b
2
= -4/4 = -1
c
1
/c
2
= -4/4 = -1
∴ We can say that,
-1 = -1 = -1
Hence, AB is parallel to CD where the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (–1, –2, 1), (1, 2, 5)
4. Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector
So, a
1
/a
2
= -2/2 = -1
b
1
/b
2
= -4/4 = -1
c
1
/c
2
= -4/4 = -1
∴ We can say that,
-1 = -1 = -1
Hence, AB is parallel to CD where the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (–1, –2, 1), (1, 2, 5)
4. Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector
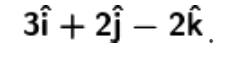 Solution:
Solution:
 5. Find the equation of the line in vector and in Cartesian form that passes through the point with
position vector
5. Find the equation of the line in vector and in Cartesian form that passes through the point with
position vector
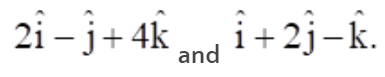 is in the direction
Solution:
is in the direction
Solution:
 6. Find the Cartesian equation of the line which passes through the point (–2, 4, –5) and parallel to the line given by
6. Find the Cartesian equation of the line which passes through the point (–2, 4, –5) and parallel to the line given by
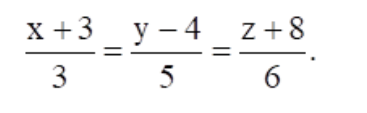 Solution:
Given:
The points (-2, 4, -5)
We know that the Cartesian equation of a line through a point (x
1
, y
1
, z
1
) and having direction ratios a, b, c is
Solution:
Given:
The points (-2, 4, -5)
We know that the Cartesian equation of a line through a point (x
1
, y
1
, z
1
) and having direction ratios a, b, c is
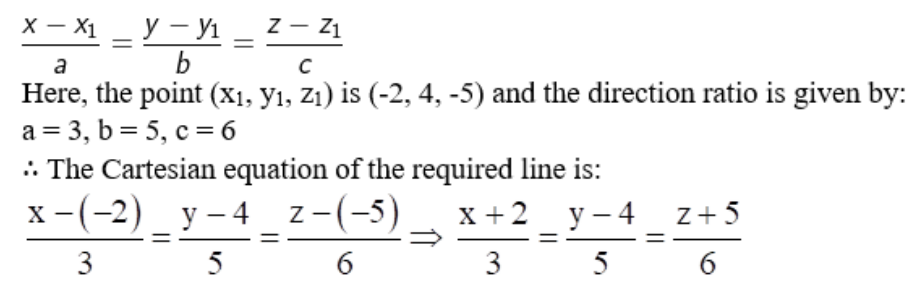 7. The Cartesian equation of a line is
7. The Cartesian equation of a line is
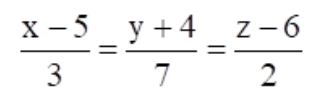 Write its vector form.
Solution:
Write its vector form.
Solution:
 So when comparing this standard form with the given equation, we get
x
1
= 5, y
1
= -4, z
1
= 6 and
l = 3, m = 7, n = 2
So when comparing this standard form with the given equation, we get
x
1
= 5, y
1
= -4, z
1
= 6 and
l = 3, m = 7, n = 2
 8. Find the vector and the Cartesian equations of the lines that passes through the origin and (5, –2, 3).
Solution:
8. Find the vector and the Cartesian equations of the lines that passes through the origin and (5, –2, 3).
Solution:

 9. Find the vector and the Cartesian equations of the line that passes through the points (3, –2, –5), (3, –2, 6).
Solution:
9. Find the vector and the Cartesian equations of the line that passes through the points (3, –2, –5), (3, –2, 6).
Solution:

 10.
Find the angle between the following pairs of lines:
10.
Find the angle between the following pairs of lines:
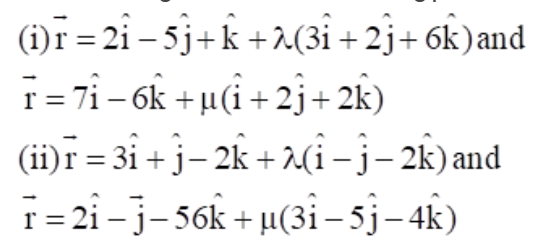 Solution:
Solution:

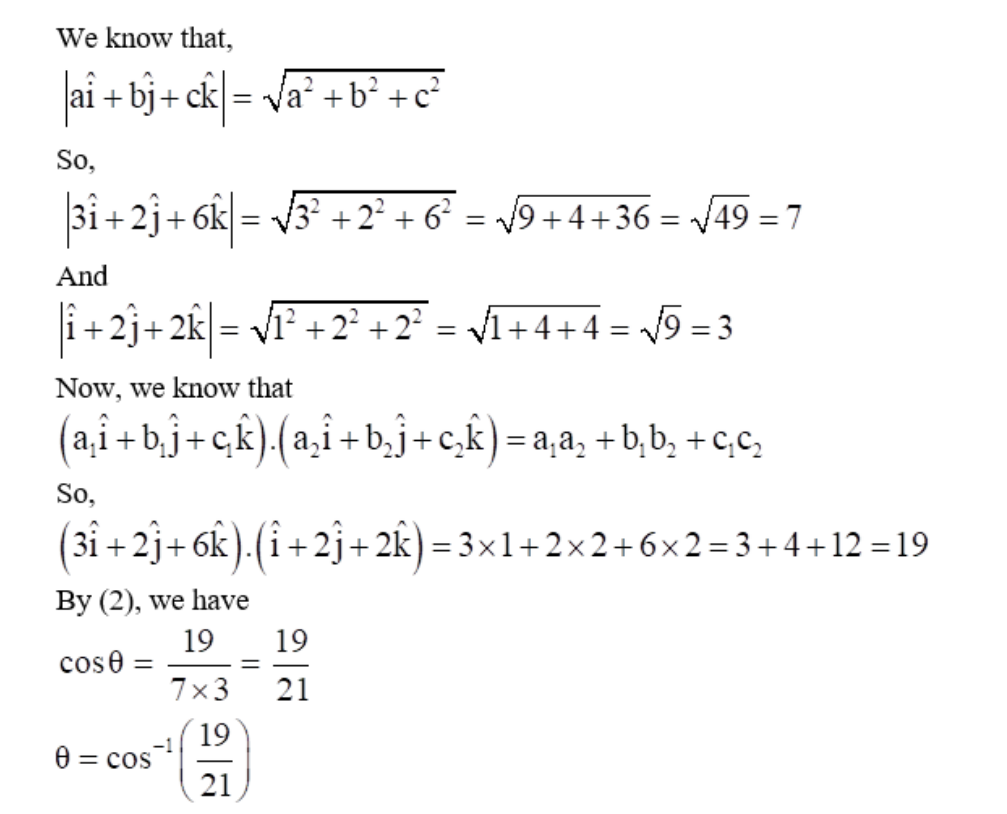 So,
So,
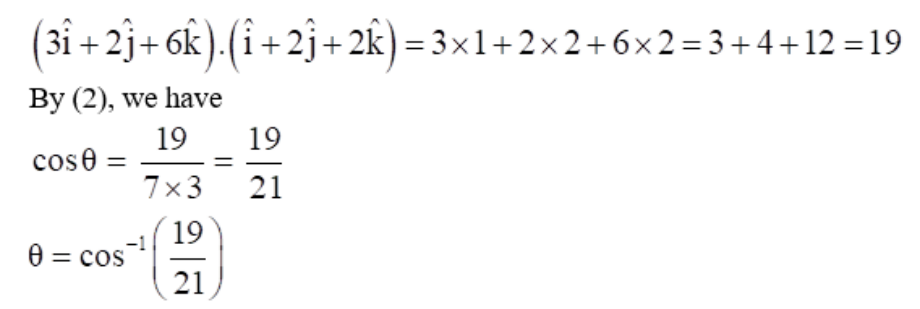
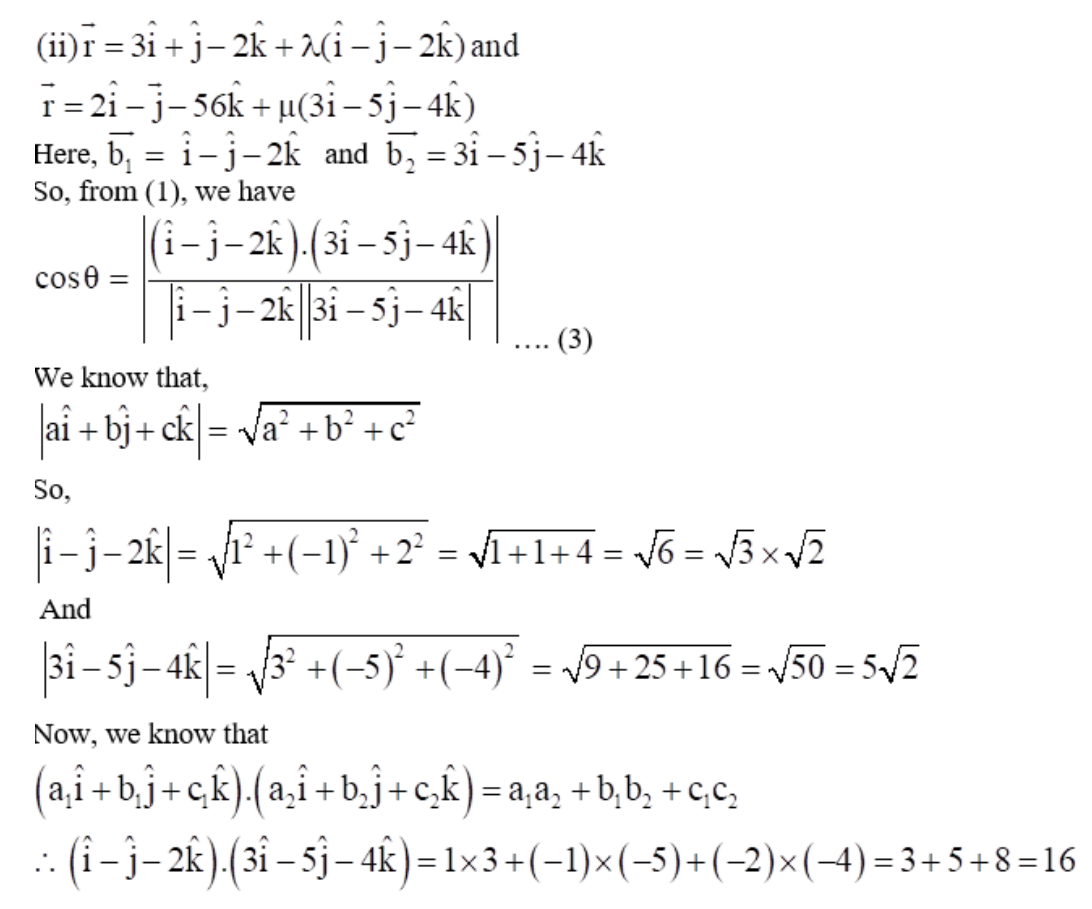 By (3), we have
By (3), we have
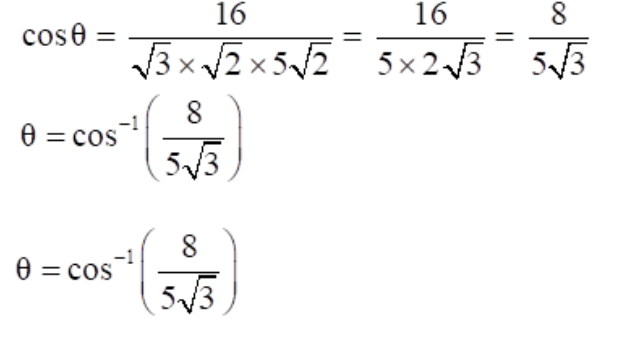 11. Find the angle between the following pair of lines:
11. Find the angle between the following pair of lines:
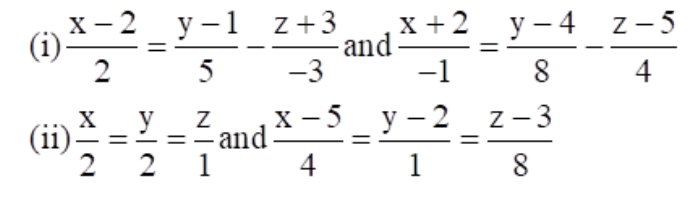 Solution:
Solution:



Topics Included in NCERT Solutions for Class 12 Maths Chapter 11
This article from Physics Wallah includes the following topics of Three Dimensional Geometry as mentioned by NCERT.11.1 Introduction
11.2 Direction Cosines and Direction Ratios of a Line
11.2.1 Relation between the direction cosines of a line
11.2.2 Direction cosines of a line passing through two points
11.3 Equation of a Line in Space
11.3.1 Equation of a line through a given point and parallel to a given vector b.
11.3.2 Equation of a line passing through two given points
11.4 Angle between Two Lines
11.5 Shortest Distance between Two Lines
11.5.1 Distance between two skew lines
11.5.2 Distance between parallel lines
11.6 Plane
11.6.1 Equation of a plane in normal form
11.6.2 Equation of a plane perpendicular to a given vector, passing through a given point
11.6.3 Equation of a plane passing through three non-collinear points
11.6.4 Intercept form of the equation of a plane
11.6.5 Plane passing through the intersection of two given planes
11.7 Coplanarity of Two Lines
11.8 Angle between Two Planes
11.9 Distance of a Point from a Plane
11.10 Angle between a Line and a Plane
NCERT Solutions for Class 12 Maths Chapter 11- Three Dimensional Geometry
The chapter on Three Dimensional Geometry forms a part of Unit Vectors and the solutions have been given as per the CBSE syllabus for the 2023-24 session. They carry 14 marks of the total. A miscellaneous exercise is given as well which helps students form a clearer understanding of Three Dimensional Geometry concepts. Here are some of the concepts that have been discussed in the Three Dimensional Geometry Class 12 solutions.- Direction cosines of a line are the cosines of the angles made by the line with the positive directions of the coordinate axes.
- If l, m, n are the direction cosines of a line, then l 2 + m 2 + n 2 = 1
- Direction ratios of a line are the numbers which are proportional to the direction cosines of a line.
- Skew lines are lines in space which are neither parallel nor intersecting. They lie in different planes.
- Angle between skew lines is the angle between two intersecting lines drawn from any point (preferably through the origin) parallel to each of the skew lines.
- If l 1 , m 1 , n 1 and l 2 , m 2 , n 2 are the direction cosines of two lines; and θ is the acute angle between the two lines; then cosθ = |l 1 l 2 + m 1 m 2 + n 1 n 2 |
NCERT Solutions for Class 12 Maths Chapter 11- Three Dimensional Geometry, Its Key Features
When students practice with our Three Dimensional Geometry Class 12 solutions, they can form a clear understanding of the following concepts—- Direction cosines and direction ratios of a line joining two points.
- Cartesian equation and vector equation of a line,
- Coplanar and skew lines, the shortest distance between two lines.
- Cartesian and vector equation of a plane.
- The angle between (i) two lines, (ii) two planes, (iii) a line and a plane. Distance of a point from a plane
NCERT Solutions for Class 12 Maths Chapter 11 FAQs
What is Three Dimensional Geometry?
How can I learn Three Dimensional Geometry well?
Do the solutions here help score well in the board exams?
What do students learn from this article?
Is regular practice necessary to sharpen your skills of Three Dimensional Geometry?












