Motion In One Dimension
Kinematics of Class 11
Displacement
The displacement of a particle is defined as the difference between its final position and its initial position. We represent the displacement as Δx.
Δx = xf− xi
The subscripts iand f refer to be initialand final positions. These are not necessarily the positions from which the particle starts its motion nor where its motion ceases. The i and f designate the particular initial and final positions we are considering out of the entire motion of the object. Notethe order : final position minus initial position . Whenever we calculate “delta” anywhere, we always take the final value minus the initial value.
Average Velocity and Average Speed
The average velocity of an object travelling along the x−axis is defined as the ratio of its displacement to the time taken for that displacement.
vav=
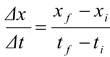 (7.1)
(7.1)
The average speed of a particle is defined as the ratio of the total distance travelled to the time taken.
Average speed = Total distance travelled/Δt
Note that velocity and speed have different meanings.
Example : 7.1
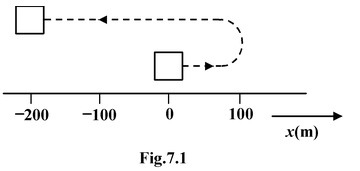
A bird flies toward east at 10 m/s for 100 m. It then turns around and flies at 20 m/s for 15 s. Find
(a) its average speed
(b) its average velocity
|
Solution Let us take the xaxis to point east. A sketch of the path is shown in the figure. To find the required quantities, we need the total time interval. The first part of the journey took Δt1= (100 m)/ (10 m/s) = 10 s, and we are given Δt2= 15 s for the second part. Hence the total time interval is |
|
Δt= Δt 1 + Δt 2 = 25 s
The bird flies 100 m east and then (20 m/s) (15 s) = 300 m west
(a)Average speed = Distance/Δt = 100m + 300 m/25s = 16m/s
(b)The net displacement is
Δx= Δx 1 + Δx 2 = 100 m − 300 m = −200 m
So that
vav= Δx/Δt = -200m/25s = -8 m/s
The negative sign means that vavis directed toward the west.
CAUTIONSometimes students try to calculate the average velocity by just adding the two given velocities and dividing by two. This procedure is wrong, and it can be clearly illustrated with the following example. A college student drives a car 1 kilometer at 30 kmph. How fast must the student drive a second kilometer in order to average 60 kmph for the 2 minute trip. If you believe that the average velocity is the average of the velocities, then the answer will be 90 kmph because 30 + 90/2 = 60 kmph. But the correct answer is “not possible”. There is no way the student can get average 60 kmph for the trip! Sixty kmph means 1 km/min. In order to average 60 kmph for 2 km, the trip must be driven in 2 min. But going the first kilometer at 30 kmph takes 2 min. So the driver has no time left at all to go the second kilometer. |
Example: 7.2
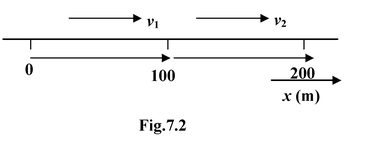
A jogger runs his first 100 m at 4 m/s and the second 100 m at 2 m/s in the same direction. What is the average velocity ?
|
Solution A sketch of his motion is shown in figure. His net displacement Δx= Δx 1 + Δx 2 = 100 m + 100 m = 200 m |
|
The first half took
Δt1= (100 m)/(4 m/s) = 25 s,
while the second took
Δt1= (100 m)/(2 m/s) = 50 s,
The total time interval is
Δt= Δt 1 + Δt 2 = 75 s
Therefore, his average velocity is
vav= Δx/Δt = 200m/75s = 2.67 m/s
Since 2.67 ≠ 1/2 (4+2), we see that the average velocity is not, in general, equal to the average of the velocities.
Average Acceleration is defined as the ratio of the change in velocity to the time taken.
a
av
=
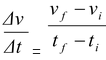 (7.2)
(7.2)
Instantaneous Velocity is defined as the value approached by the average velocity when the time interval for measurement becomes closer and closer to zero, i.e. Δt → 0. Mathematically
v(t) =
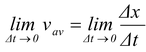
The instantaneous velocity function is the derivative with respect to the time of the displacement function.
v(t)=
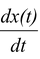 (7.3)
(7.3)
Instantaneous Acceleration is defined analogous to the method for defining instantaneous velocity. That is, instantaneous acceleration is the value approached by the average acceleration as the time interval for the measurement becomes closer and closer to zero.
The Instantaneous acceleration function is the derivative with respect to time of the velocity function
a(t)=
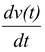 (7.4)
(7.4)
Example: 7.3
The position of a particle is given by
x= 40 − 5t− 5t 2 , where x is in metre and t is in second
(a) Find the average velocity between 1 s and 2 s
(b) Find its instantaneous velocity at 2 s
(c) Find its average acceleration between 1 s and 2 s
(d) Find its instantaneous acceleration at 2 s
Solution
(a) Att = 1 s; xi= 30 m
t = 2 s; xf= 10 m
vav=
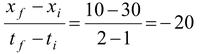 m/s
m/s
(b) v = dx/dt = -5 -10t
At t= 2 s; v= −5−10(2) = −25 m/s
(c) At t = 1 s; v = −5−10 (1) = −15 m/s
t = 2 s; v = −5−10 (1) = −25 m/s
aav=
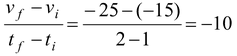 m/s2
m/s2
(d)a= dv/dt = −10 m/s 2