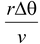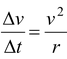Circular Motion
Kinematics of Class 11
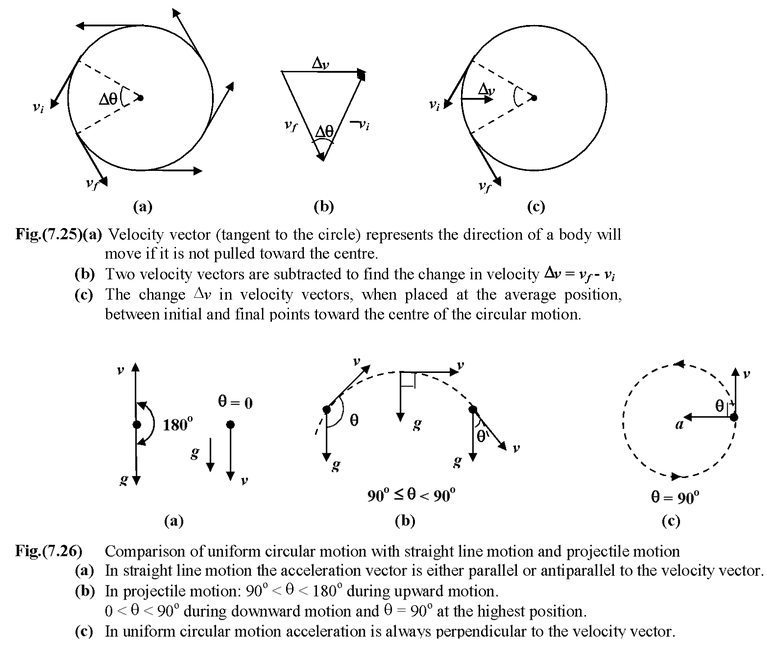
In its simplest kind, a particle moves in a circular path of constant radius with constant speed. Although the magnitude of the velocity vector remains constant but the direction of the velocity vector changes direction continuously as shown in Fig. (7.25). Thus a particle is continuously accelerated. Since the acceleration produces a change only in the direction of the velocity vector, therefore, it must always be at right angles to the direction of motion. It is because any component in the direction of the motion would produce a change in speed of the particle.
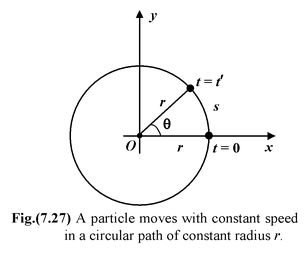
Let us consider a particle which moves in a circular path of radius r and constant speed v as shown in Fig. (7.27). In a time t the line joining the particle and the centre subtends an angleθ which is given by
θ(radian) =
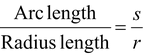
On differentiating both sides, we get
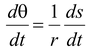
or ω = v/r (7.26)
|
where ω is the angular speed From Fig.(7.25 b), Δθ = (Δv/v) |vf| = |vi| = v
Since Δs = vΔt = rΔθ⇒Δt =
Thus, acceleration, a =
Note that this acceleration point inward toward the centre of the circle. It is called centripetal acceleration (means ‘centre seeking’) |
|
Alternatively the magnitude of the centripetal acceleration can be found using calculus and vector notation.
|
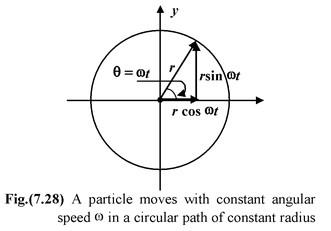
r = xi + yj r = r cos θi + r sin θj r(t) = r cos ωti + r sinωtj v(t) = dr/dt = −rω sin ωti + rω cosωtj v= ωr a(t) = dv(t)/dt = −rω 2 cosωti−rω 2 sinωtj a(t) = −ω 2 r(t) a = ac= ω 2 r ac= v 2 /r |
|
To summarize, an object moving in uniform circular motion at radius r and constant angular speed ω has
1.a constant linear speed v = rω tangent to the circle and
2.a centripetal acceleration ac= ω2r = v2/r directed inward toward the centre of the circle
Example: 7.15
A stone tied to the end of a string 75 cm long is whirled in a horizontal circle with a constant speed. If the stone make 15 revolutions in 25s. What is the magnitude and direction of acceleration of the stone ?
Solution
Radius of the circular path, r = 75 cm = 0.75 m
Number of revolutions per second n = 15/25 = 0.6s -1
Now, v = 2πnr
orv = 2(3.14) (0.6) (0.75) = 2.83 m/s
Magnitude of acceleration, a = v 2 /r = (2.83) 2 /0.75 = 10.68 m/s2
The direction of acceleration is radially inwards.
Tangential and Normal Components of Acceleration in Two Dimensions
1.The velocity vector is always tangential to the path
2.The acceleration vector may have two components: one tangential to the path and one perpendicular to the path.
(a)The component of the acceleration parallel to the path is due to a change in speed. When the speed is increasing, the tangential component atpoints in the same direction as the velocity; when the speed is decreasing, the tangential component points opposite to the velocity.
(b)When the path of an object curves, there is a component of the acceleration perpendicular to the velocity. This component of the acceleration acpoints toward the inside of the curve.
(c)The total acceleration is the vector sum of the tangential and centripetal components.