Atomic Nucleus

ATOMIC NUCLEUS

The atomic nucleus consists of two types of elementary particles, viz. Protons and neutrons. These particles are called nucleons.

The proton (denoted by p) has a charge +e and a mass m p ≈ 1.6726 × 10 -27 kg, which is approximately 1840 times larger than the electron mass. The proton is the nucleus of the simplest atom with Z = 1, viz. the hydrogen atom.

The neutron (denoted by n) is an electrically neutral particle (its charge is zero). The neutron mass m n ≈ 1.6749 × 10 -27 kg. The fact that the neutron mass exceeds the proton mass by about 2.5 electron masses is of essential importance. It follows from this that the neutron in free state (outside the nucleus) is unstable (radioactive). During the time equal on the average to 12 min, the neutron spontaneously transforms to the proton by emitting an electron (e - ) and a particle called the antineutrino ( v ). This process can be schematically written as follows:

n → p + e - + v .

The most important characteristics of the nucleus are the charge number
Z (coinciding with the atomic number of the element) and the mass number A. The charge number Z is equal to the number of protons in the nucleus, and hence it determines the nuclear charge equal to Ze. The mass number A is equal to the number of nucleons in the nucleus (i.e. to the total number of protons and neutrons).

Nuclei are symbolically designated as Z X A

where X stands for the symbol of a chemical element. For example, the nucleus of the oxygen atom is symbolically written as 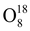or 8 O 18 .

Most of the chemical element have several types of atoms differing in the number of neutrons in their nuclei. These varieties are called isotopes. For example, oxygen has three stable isotopes: 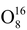, 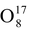and 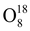. In addition to stable isotopes, there also exist unstable (radioactive) isotopes.

Atomic masses are specified in terms of the atomic mass unit or unified mass unit (u). The mass of a neutral atom of the carbon isotope 6 C 12 is defined to be exactly 12 u.

1u = 1.66056 × 10 -27 kg = 931.5 MeV

Example 16.14

(a) Calculate the value of 1 u from Avogadro’s number.

(b) Determine the energy equivalent of 1u.

Solution

(a) One mole of C 12 has a mass of 12 g and contains Avogadro’s number, N A , of atoms.

By definition, each C 12 has a mass of 12 u.

Thus, 12 g corresponds to 12 N A u   which means

1u =

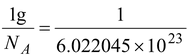
or 1u = 1.66056 × 10 -27 kg

(b) From Einstein relation  E = mc 2

∴ E = (1.66056 × 10 -27 ) (3 × 10 8 ) 2 = 1.4924 × 10 -10 J

Since 1eV = 1.6 × 10 -19 J

∴ E = 931.5 MeV

Hence 1u = 931.5 MeV

The shape of nucleus is approximately spherical and its radius is approximately related to the mass number by

R ≈ 1.2 A 1/3 fm

where 1 fermi (fm) = 10 -15 m

Example 16.15

Find the mass density of the oxygen nucleus 8 O 16 .

Solution

Volume V = 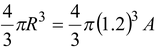= 1.16 × 10 -43 m 3

Mass of oxygen atoms (A = 16) is approximately 16 u.

Therefore, density is ρ = m/v

or ρ = 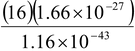= 2.3 × 10 17 kg/m 3

This is 10 14 times the density of water.

Binding Energy

The rest mass of the nucleus is smaller than the sum of the rest masses of nucleons constituting it. This is due to the fact that when nucleons combine to form a nucleus, the binding energy of nucleons is liberated. The binding energy is equal to the work that must be done to split the nucleus into particles constituting it.

The difference between the total mass of the nucleons and the mass of the nucleus is called the mass defect of the nucleus:

Δm = [Zm p + (A − Z)m n ] − m nuc .

Multiplying the mass defect by the square of the velocity of light, we can find the binding energy of the nucleus:

BE = Δmc 2 = [(Zm p + (A – Z)m n ) – m nuc ]c 2 J (16.25)

If the masses are taken in atomic mass unit, the binding energy is given by

BE = [Zm P + (A – Z)m n – m nuc ]931.5  MeV (16.26)

Dividing the binding energy by the number A of nucleons in the nucleus, we obtain the binding energy per nucleon. Fig.(16.13) shows the dependence of the binding energy per nucleon BE/A on the mass number A of the nucleus. Nucleons in nuclei with mass numbers from 50 to 60 have the highest binding energy. The binding energy per nucleon for these nuclei amounts to 8.7 MeV and gradually decreases with increasing A. For the heaviest natural element − uranium − it amounts to 7.5 MeV. Figure shows that when a heavy nucleus (with A ≈ 240) splits into two nuclei with A = 120, the released energy is of the order of 1 MeV per nucleon i.e. 240 MeV per parent nucleus. It should be mentioned for comparison that when a carbon atom is oxidized (burnt) to CO 2 , the energy of the order of 5 eV is liberated, which is smaller than the energy released in fission of a uranium nucleus by a factor of 50 millions.

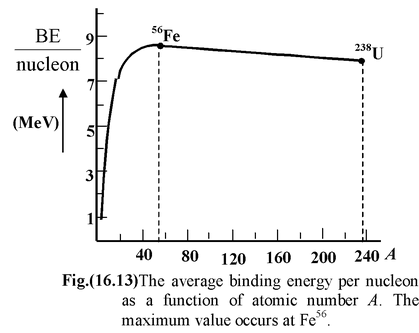
It also follows from Fig(16.13) that the fusion (synthesis) of light nuclei into one should be accompanied by the liberation of a huge energy. For example, the fusion of two nuclei of heavy hydrogen ₁ H ² (this nucleus is called a deuteron) into a helium nucleus ₂ He ⁴ would yield an energy equal to 24 MeV.

The forces binding nucleons in a nucleus manifest themselves at distances < 10 -15 m.
In order to bring together two positively charged deuterons to such a distance, their Coulomb repulsion should be overcome. For this, the deuterons must have a kinetic energy equivalent to their mean energy of thermal motion at a temperature of the order of 10 9 K. For this reason, the fusion reaction of nuclei is also called a thermonuclear reaction. Actually, some thermonuclear reactions may occur at a temperature of the order of 10 7 K. This is due to the fact that there is always a certain number of nuclei whose energy considerably exceeds the mean value.

Example  16.16

Find the binding energy of  ? Also find the binding energy per nucleon.

Solution

One atom of 6 12 C consists of 6 protons, 6 electrons and 6 neutrons. The mass of the uncombined protons and electrons is the same as that of six  atoms (if we ignore the very small binding energy of each proton-electron pair).

Mass of six  atoms = 6 × 1.0078 = 6.0468 u

Mass of six neutrons = 6 × 1.0087 = 6.0522 u

Total mass of component particles = 12.0990 u

Mass of 6 12 C atom = 12.00004

Mass defect = 0.0990 u

Binding energy = (931)(0.099) = 92 MeV

Binding energy per nucleon = 92/12 = 7.66 MeV

Example 16.17

A neutron breaks into a proton and electron. Calculate the energy produced in this reaction in MeV. Mass of an electron = 9 × 10 -31 kg, Mass of proton = 1.6725 × 10 -27 kg, Mass of neutron 1.6747 × 10 -27 kg. Speed of light = 3 × 10 8 m/s.

Solution

o n 1 → 1 H 1 + -1 e o

Mass defect (Δm) = [Mass of neutron – (mass of proton + mass of electron)]

= [1.6747 × 10 -27 – (1.6725 × 10 -27 + 9 × 10 -31 )]

= 0.0013 × 10 -27 kg

∴ Energy released   Q = Δm c 2

Q = (0.0013 × 10 -27 ) × (3 × 10 8 ) 2 = 1.17 × 10 -13 J

= 1.17 x 10 ^-13 /1.6 x 10 ^-19 = 0.73 × 10 6 eV = 0.73 MeV

NUCLEAR  REACTION

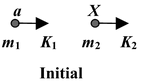
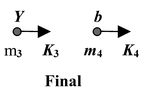
A nuclear reaction in which a collision between particle a and nucleus X produces Y and particle b is represented as a + X → Y + b

The reaction is sometimes expressed in the shorthand notation X(a, b)Y.

Reactions are subjected to the restrictions imposed by the conservation of charge, energy, momentum and angular momentum.

Energy of A Reaction

Initial energy: E i = m 1 c 2 + m 2 c 2 + K 1 + K 2

Final energy: E f = m 3 c 2 + m 4 c 2 + K 3 + K 4

Since E i = E f (energy conservation)

∴ [(m 1 + m 2 ) - (m 3 + m 4 )]c 2 = (K 3 + K 4 ) - (K 1 + K 2 )

The energy, that is released or absorbed in a nuclear reaction is called the Q - value or disintegration energy of the reaction.

Q = [(m 1 + m 2 ) - (m 3 + m 4 )]c 2 J (16.27 a)

or Q = [(m 1 + m 2 ) - m 3 + m 4 )] 931.5 u (16.27 b)

If Q is positive, rest mass energy is converted to kinetic mass energy, radiation mass - energy or both, and the reaction is exoergic.

If Q is negative, the reaction is endoergic. The minimum amount of energy that a bombarding particle must have in order to initiate an endoergic reaction, is called Threshold Energy E th .

E th = -Q 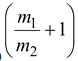(16.28)

where m 1 = mass of the projectile

m 2 = mass of the target.

Example 16.18

Neon - 23  beta decays in the following way :

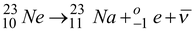
Find the minimum and maximum  kinetic energy that the beta particle 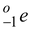can have.  The atomic masses of 23 Ne and 23 Na are 22.9945 u and 22.9898 u, respectively.

Solution

Reactant Products

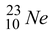22.9945 - 10m e 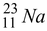22.9898 - 11 m e

-m e

Total 22.9945 – 10 m e Total 22.9898 – 10 m e

Mass defect = 22.9945 - 22.9898 = 0.0047 u

Q = (0.0047)(931) = 4.4 MeV

The β - particle and neutrino share this energy. Hence the energy of the β-particle can range from 0 to 4.4 MeV.

Example 16.19

How much energy must a bombarding proton possess to cause the reaction.

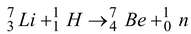
Solution

Since the mass of an atom include the masses of the atomic electrons, the appropriate number of electron masses must be subtracted from the given values.

Reactants Products

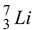7.01600 - 3 m e 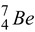7.01693 - 4m e

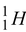1.0783 - 1 m e 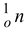1.0866

Total 8.02383 - 4 m e Total 8.02559 - 4 m e

The Q-value of the reaction

Q = -0.00176 u = −1.65 MeV

The energy is supplied as kinetic energy of the bombarding proton. The incident proton must have more than this energy because the system must possess some kinetic energy even after the reaction, so that momentum is conserved.

With momentum conservation taken into account, the minimum kinetic energy that the incident particle can be found with the formula.

E th = - 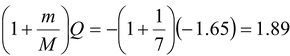MeV

Example 16.20

In a nuclear reactor, fission is produced in 1 g for U 235 (235.0439 u) in 24 hours by a slow neutron (1.0087 u). Assume that 35 Kr 92 (91.8973 u) and 56 Ba 141 (140.9139 amu) are produced in all reactions and no energy is lost.

(a) Write the complete reaction

(b) Calculate the total energy produced in kilowatt hour. Given 1 u = 931 MeV.

Solution

The nuclear fission reaction is 92 U 235 + o n 1 → 56 Ba 141 + 36 Kr 92 + 3 o n 1

Mass defect Δm = [(m u + m n ) – (m B a + m Kr + 3m n )]

Δm = 256.0526 – 235.8373 = 0.2153 u

Energy released  = 0.2153 × 931 = 200 MeV

Number of atoms in 1 g = 6.02 x 10 ²³ /235= 2.56 × 10 21

Energy released in fission of 1 g of U 235 is Q = 200 × 2.56 × 10 21 = 5.12 × 10 23 MeV

= (5.12 × 10 23 ) × (1.6 × 10 -13 ) = 8.2 × 10 10 J

=  8.2 x 10 ¹⁰ /3.6 x 10 ⁶ = 2.28 × 10 4 kWh

Example 16.21

It is proposed to use the nuclear fusion reaction:

1 H 2 + 1 H 2 = 2 He 4

in a nuclear reactor of 200 MW rating. If the energy from above reaction is used with a 25% efficiency in the reactor, how many grams of deuterium will be needed per day. (The masses of 1 H 2 and 2 He 4 are 2.0141 and 4.0026 u respectively).

Solution

Energy released in the nuclear fusion is

Q = Δmc 2 = Δm(931)MeV

⇒ Q = (2 × 2.0141 – 4.0026) × 931MeV = 23.834 MeV = 23.834 × 10 6 eV

Since efficiency of reactor is 25%

So effective energy used = 25 / 100 × 23.834 × 10 6 × 1.6 × 10 -19 J = 9.534 × 10 -13 J

Since the two deuterium nucleus are involved in a fusion reaction, therefore, energy released per deuterium is 9.534 x 10 ^-13 /2

For 200MWpower per day

number of deuterium nuclei required = 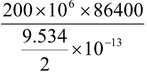= 3.624 × 10 25

Since 2g of deuterium constitute 6 × 10 23 nuclei, therefore amount of deuterium required is

g = 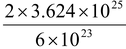= 120.83 g/day