
CLASSIFICATION OF NUMBERS
Number system of Class 9
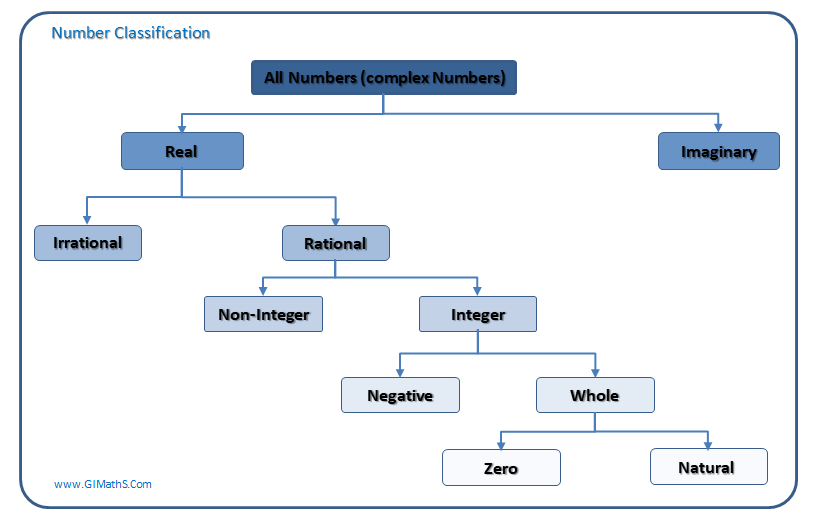
Natural numbers:
Set of all non-fractional number from 1 to +
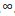 , N = {1,2,3,4,....}.
, N = {1,2,3,4,....}.
Whole numbers :
Set of numbers from 0 to
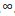 , W = {0,1,2,3,4,.....}.
, W = {0,1,2,3,4,.....}.
Integers :
Set of all-non fractional numbers from – ∞ to
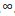 , I or Z = (...., -3,-2,-1,0,1,2,3,....}.
, I or Z = (...., -3,-2,-1,0,1,2,3,....}.
Rational numbers :
These are real numbers which can be expressed in the form of p/q, where p and q are integers and q is not 0.
e.g. 2/3, 37/15, -17/19.
-
All natural numbers, whole numbers and integers are rational.
-
Rational numbers include all Integers (without any decimal part to it), terminating fractions (fractions in which the decimal parts terminating e.g. 0.75, - 0.02 etc.) and also non-terminating but recurring decimals e.g. 0.666...., -2.333....., etc.
Fractions:
(a) Common fraction: Fractions whose denominator is not 10.
(b) Decimal fraction: Fractions whose denominator is 10 or any power of 10.
(c) Proper fraction: Numerator < Denominator i.e. 1/4,3/4.
(d) Improper fraction: Numerator > Denominator i.e. 4/3,5/4
(e) Mixed fraction:
Consists of integral as well as fractional part i.e.
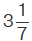
(f) Compound fraction:
Fraction whose numerator and denominator themselves are fractions. i.e.
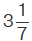 .
.
-
Improper fraction can be written in the form of mixed fractions.
(v) Irrational Numbers: All real number which are not rational are irrational numbers. These are non-recurring as well as non-terminating type of decimal numbers e.g. √5, √11, √21 etc.
(vi) Real numbers: Number which can represent actual physical quantities in a meaningful way are known as real numbers. These can be represented on the number line. Number line in geometrical straight line with arbitrarily defined zero (origin).
(vii) Prime number : All natural numbers that have one and itself only as their factors are called prime numbers i.e. prime numbers are exactly divisible by 1 and themselves. e.g. 2,3,5,7,11,13,17,19,23....etc. If P is the set of prime number then P = {2,3,5,7....}.
(viii) Composite numbers : All natural number, which are not prime are composite numbers. If C is the set of composite number then C = {4,6,8,9,10,12,.....}.
-
1 is neither prime nor composite number.
(ix) Co-prime numbers : If the H.C.F. of the given numbers (not necessarily prime) is 1 then they are known as co-prime numbers. e.g. 4, 9, are co-prime as H.C.F. of (4, 9) = 1.
-
Any two consecutive numbers will always be co-prime.
(x) Even Numbers : All integers which are divisible by 2 are called even numbers. Even numbers are denoted by the expression 2n, where n is any integer. So, if E is a set even numbers, then E = {...., -4, -2, 0, 2, 4,....}.
(xi) Odd Numbers: All integers which are not divisible by 2 are called odd numbers. Odd numbers are denoted by the general expression 2n - 1 where n is any integer. If O is a set of odd numbers, then O = {...., -5, -3, -1, 1, 3, 5,....}.
(xii) Imaginary Numbers: All the numbers whose square is negative are called imaginary numbers. e.g. 3i, 4i, i, ..... where i = √-1 .
(xiii) Complex Numbers : The combined form of real and imaginary numbers is known as complex numbers. It is denoted by Z = A + iB where A is real part and B is imaginary part of Z and A, B are real number.
-
The set of complex number is the super set of all the sets of numbers.









