Real Numbers

Real Numbers of Class 10

The totality of rational numbers and irrational numbers is called the real numbers. i.e. rational numbers and irrational numbers taken together are called Real Numbers.

Every real-number is either a rational number or an irrational number.
A real number which is not rational is called an irrational number.

DIVISIBILITY RELATION:

If ‘a’ is divisible by b then we write it as b | a (b divides a)

b is a factor of a e.g. 2 is a factor of 10 (10 = 2 x 5)
b is a divisor of a .e.g. 3 is a divisor of 24 (24 = 3 × 8)
a is multiple of b e.g. 15 is multiple of 5 (15 = 3 x 5)

A non-zero integer ‘a’ is said to divide an integer ‘b’ if there exists an integer c such that
b = ac.

The integer ‘a’ is called the dividend, integer ‘b’ is known as the divisor and integer ‘c’ is known as the quotient.

If a and c are non-zero integers and b, d are any two integers, then

a | b and c | d ⇒ ac | bd
ac | bc ⇒ a | b

If a divides b, then we can write a divides – b and – a divides b. It is therefore appropriate if we consider positive divisors of positive integers only.

CLASSIFICATION OF NUMBERS:

Even Numbers: A natural number is said to be even if it is multiple of 2 or it is divisible by 2.

2, 4, 6, 8, 10, 12 ……. are examples of even numbers.

Odd Numbers: A natural number is said to be odd, if it is not even or if it is not divisible by 2.

1, 3, 5, 7, 9, ………. are examples of odd natural numbers.

Consecutive Numbers: A series of natural numbers each differing by one is called consecutive numbers.

50, 51, 52, 53 are consecutive numbers.

Prime Number: A natural number is said to be prime if it has only two different (distinct) factors namely one and itself. We say 4 and 9 are not prime whereas 2, 3, 5, 7, 11 are prime numbers.

1 is not a prime number
The only even prime number is 2.
The smallest prime number is 2.
All prime numbers are odd except 2.

Twin-prime: A pair of prime numbers is said to be twin-prime if they differ by 2.

For example (3, 5), (11, 13), (17, 19), (29, 31), (29, 31), (41, 43), (71, 73) are all twin-prime.

Composite Number: A natural number is said to be composite if it has at least three different factors. 4, 6, 12, are all composite numbers.

1 is not a composite number.
4 is the smallest composite number.
1 is neither prime nor composite.

Co-prime: A pair of numbers is said to be co-prime if the numbers have no common factor other than one.

i.e., Two numbers are said to be co-prime if and only if their highest common factor is 1.

i.e., Two numbers are co-prime or relatively prime if there is no factor common to them except 1.

e.g. The pairs of number (2, 3), (5, 9), (7, 13), (12, 17), (12, 35), (63, 26), (162, 35), ………. are co-prime and the pairs of numbers (4, 6), (45, 65), (25, 125), (60, 75) are not co-prime.

Perfect Number: A number is said to be perfect if it is equal to the sum of its factors other than itself.

e.g. 6 = (1 + 2 + 3); 28 = (1 + 2 + 4 + 7 + 14) therefore 6 and 28 are perfect numbers.

EUCLID’S DIVISION LEMMA:

Let ‘a’ and ‘b’ be any two positive integers. Then, there exists unique integers ‘q’ and ‘r’ such that a = b + r, where 0 ≤ r b. If b|a, than r = 0.

If a = bq + r, then every common divisor of a and b is a common divisor of b and r also.

1. Show that any positive odd integer is of the form 6q + 1 or, 6q + 3 or, 6q + 5, where q is some integer.

Sol. Let ‘a’ be any positive integer and b = 6. Then, by Euclid’s division lemma there exists integers ’a’ and ‘r’ such that

a = 6q + r, where 0 ≤ r < 6.

⇒ a = 6q or, a = 6q + 1 or, a = 6q + 2 or, a = 6a + 3 or, a = 6q + 4 or, a = 6q + 5.

[∴0 ≤ r < 6 ⇒ r = 0, 1,2,3,4,5]

⇒ a = 6q + 1 or, a = 6q + 3 or, a = 6q + 5.

[∴a is an odd integer, ∴ 6q, a 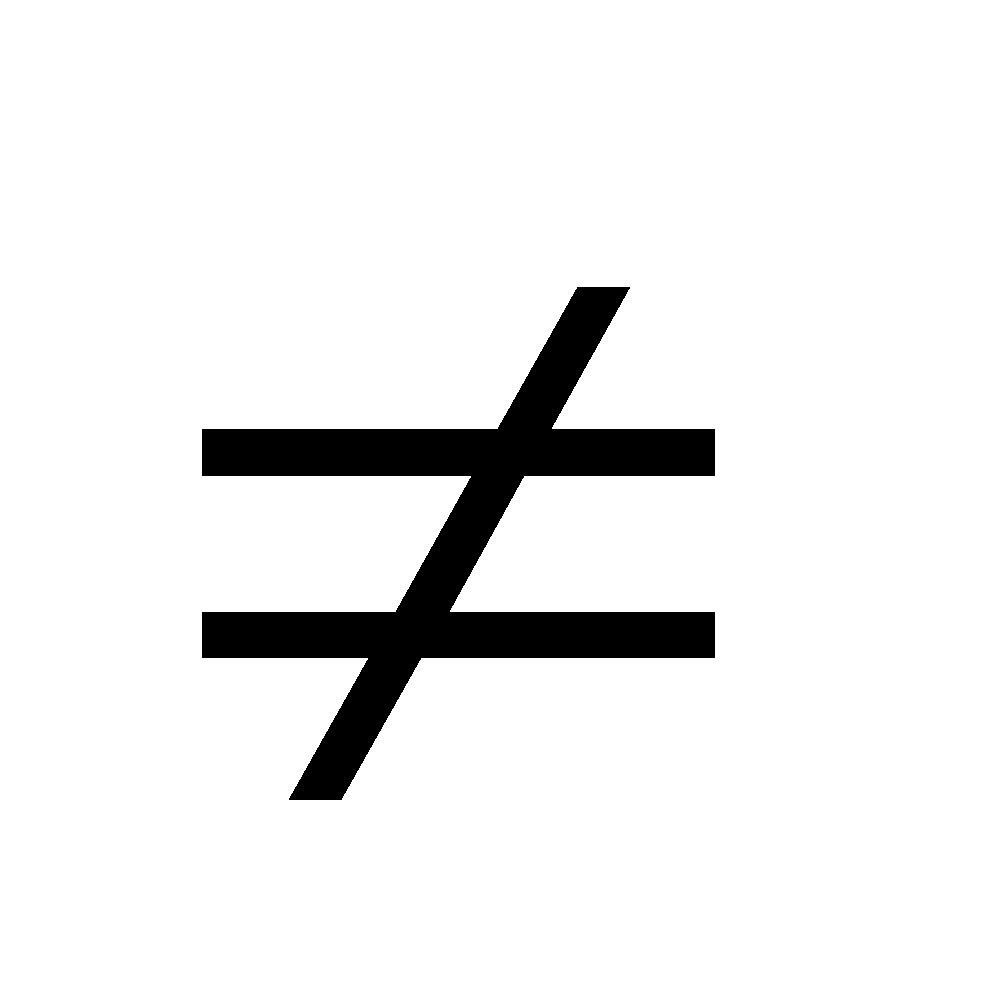Real Numbers 6q + 2, a ≠ 6q + 4]

Hence, any odd integer is of the form 6q + 1 or, 6q + 3 or, 6q + 5.

2. Use Euclid’s Division Lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9 m + 8, for some integer q.

Sol. Let x be any positive integer. Then, it is of the form 3q or, 3q + 1 or, 3 + 2.

Case - I When x = 3q

⇒ x3 = (3q)³ = 27q³ = 9(3q³) = 9m, where m = 9q³

Case - II when x = 3q + 1

⇒ x³= (3q + 1)³

⇒ x³ = 2q³ + 27q² + 9q + 1

⇒ x³ = 9q (3q² + 3q + 1) + 1

⇒ x³ = 9m + 1, where m = q (3q2 + 3q + 1).

Case - III when x = 3q + 2

⇒ x³ = (3q + 2)³

⇒ x³ = 27q³ + 54q² + 36q + 8

⇒ x³ = 9q(3q² + 6q + 4) + 8

⇒ x³ = 9m + 8, where m = 3q² + 6q + 4)

Hence, x3 is either of the form 9m of 9m + 1 or 9m + 8.

3. Use Euclid’s Division Algorithm to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.

Sol. Let x be any positive integer

Taking a = x and b = 3. So x may be either

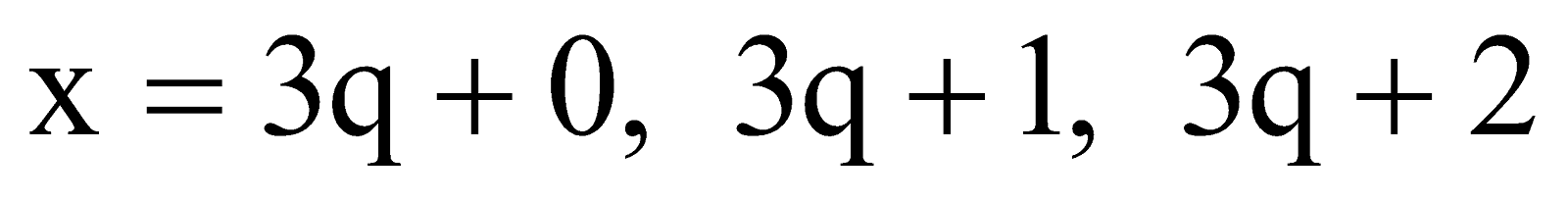Real Numbers for 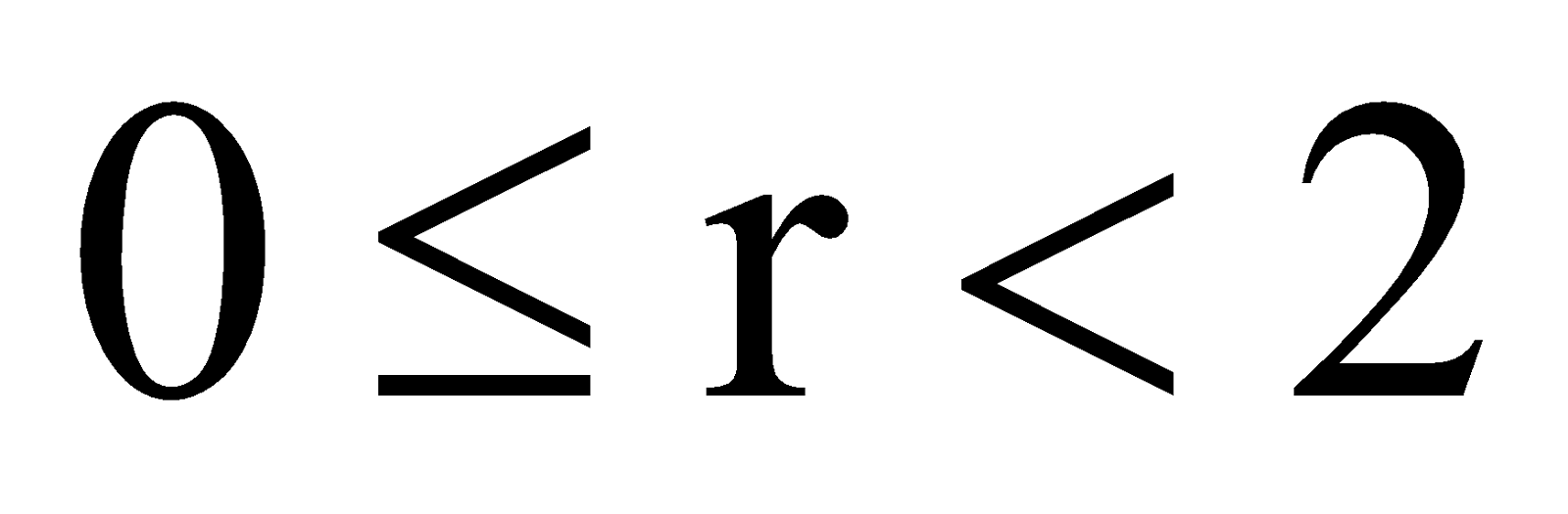[by division algorithm]

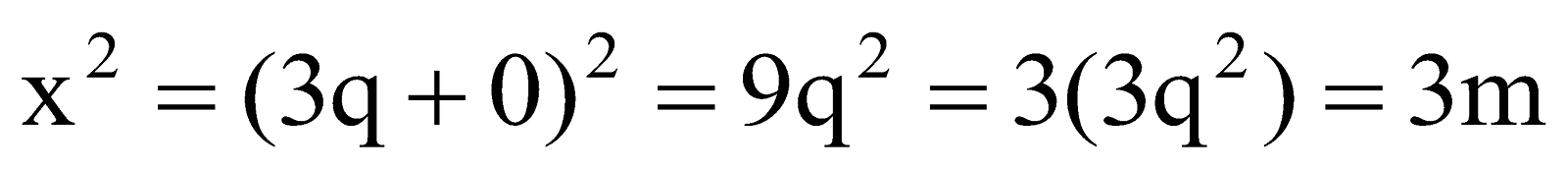⇒ Real Numbers 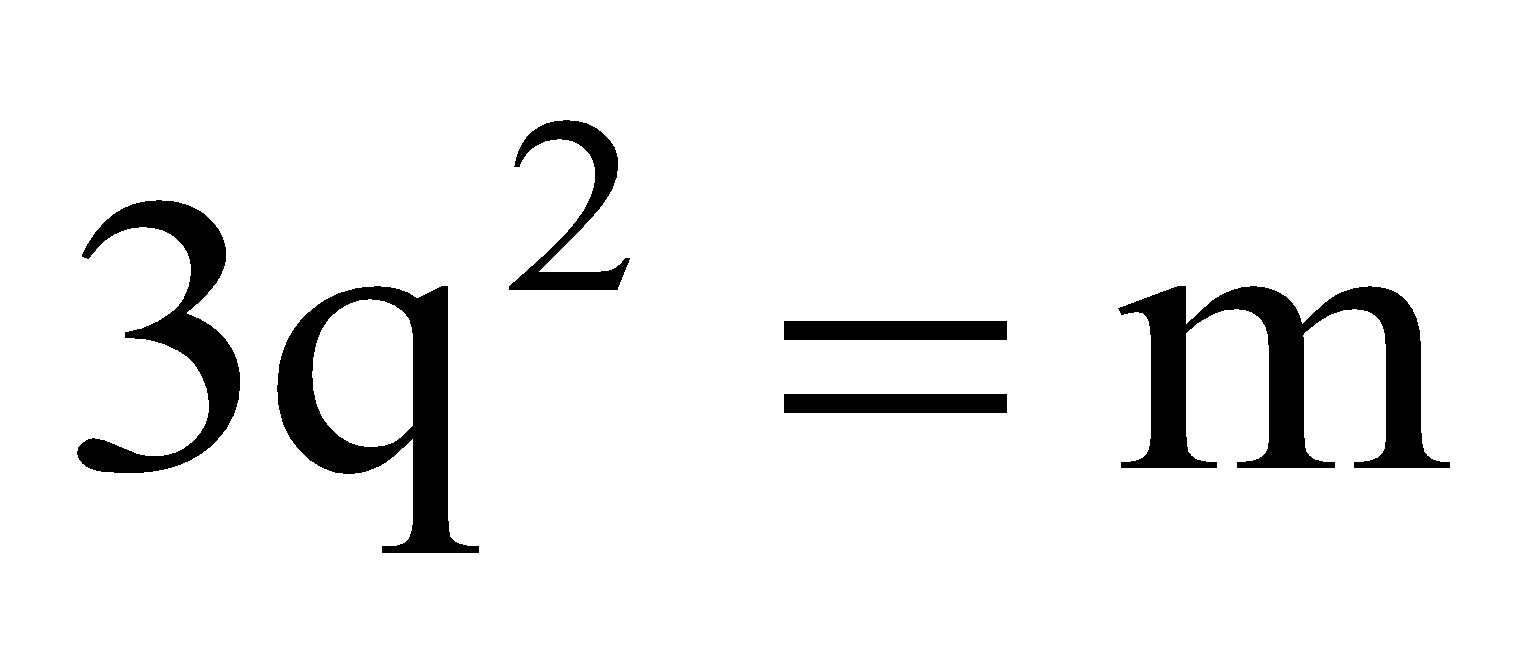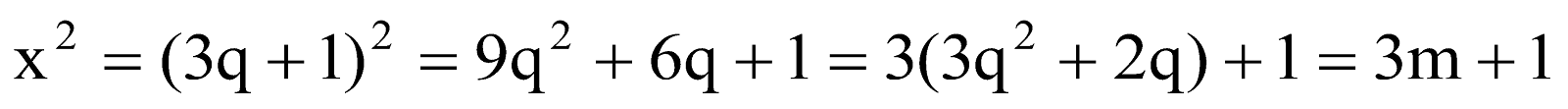[taking ]

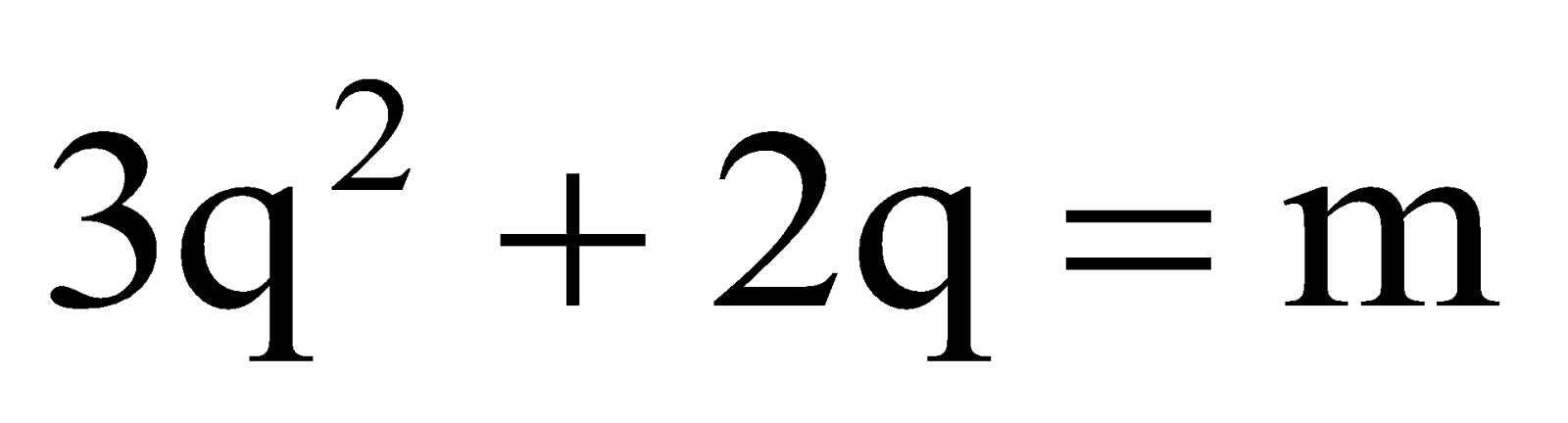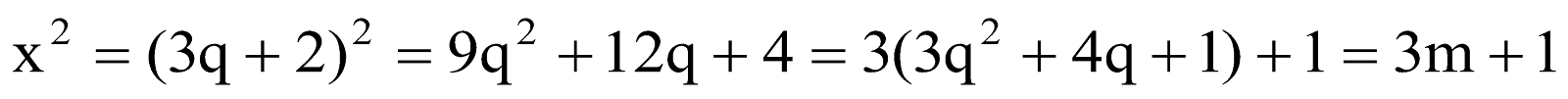
also Real Numbers

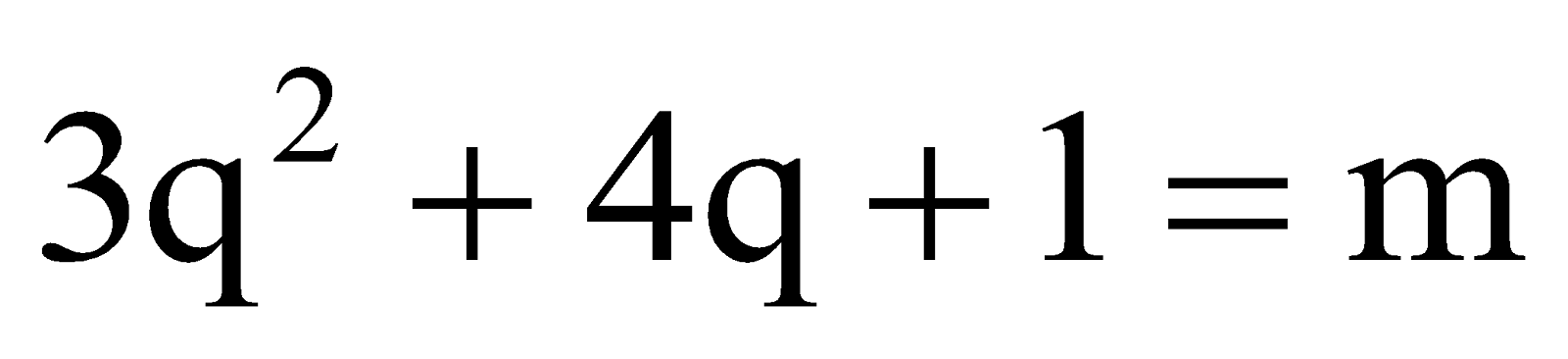[taking Real Numbers ]

Thus, we see that x² may be of the form either 3 m or 3m + 1 for some integer m.

EUCLID’S DIVISION ALGORITHM:

If ‘a’ and ‘b’ are positive integers such that a = bq + r, then every common divisor of ‘a’ and ‘b’ is a common divisor of ‘b’ and ‘r’ and vice-versa.

To obtain the HCF of two positive integers, say c and d, with c > d, follow the steps below:

Step 1: Apply Euclid's division lemma, to c and d. So, we find whole numbers, q and r such that c = dq + r, 0 ≤ r < d.
Step 2 : If r = 0, d is the HCF of c and d. If r ≠ 0. If r ≠ 0, apply the division lemma to d and r.
Step 3 : Write d = er + r1 where 0 < r-1 < r
Step 4 : Continue the process till the remainder is zero. The divisor at this stage will be the required HCF.

To find HCF of 575 and 15. Let us use Euclid’s algorithm

575 = 15 × 38 + 5

Now, consider 15 and 5 and applying Euclid’s algorithm again.

15 = 5 × 3 + 0

Here, the remainder is zero.

∴ HCF of 15 and 5 is 5.

∴ HCF of 575 and 15 is also 5.

1. Find the HCF of 128, 240 using Euclid’s Division Algorithm.

Sol. 240 = 128 × 1 + 112

128 = 112 × 1 + 16

112 = 16 × 7 + 0 → Remainder is zero.

HCF of 112 and 16 is 16.

HCF of 240 and 128 is 16.

2. What is the largest number that divides 626, 3127 and 15628 and leaves remainders of 1, 2 and 3 respectively.

Sol. Clearly, the required number is the H.C.F. of the number 626 - 1 = 625, 3127 - 2 3125 and 15628 – 3 = 15625.

15628 – 3 = 15625.

Using Euclid’s division lemma to find the H.C.F. of 625 and 3125.

3125 = 625 × 5 + 0

Clearly, H.C.F. of 625 and 3125 is 625.

Now, H.C.F. of 625 and 15625

15625 = 625 × 25 + 0

So, the H.C.F. of 625 and 15625 is 625.

Hence, H.C.F. of 625, 3125 and 15625 is 625.

Hence, the required number is 625.

3. Show that only one of the numbers (n + 2), n and (n + 4) is divisible by 3.

Sol. Let n be any positive integer.

On dividing n by 3, let q be the quotient and r be the remainder.

Then, by Euclid’s division lemma, we have

n = 3q + r where 0 ≤ r < 3

⇒ n = 3q + r where r = 0,1 or 2

⇒ n = 3q (where r = 0), n = 3q +1 (when r = 1

and n = 3q +2 (when r = 2)

The following table shows the divisibility of n, n + 2 and n + 4 by 3.

Case 1:	Positive integer (n)	N	n + 2	n + 4
	When n = 3q	3q	(3q) + 2	(3q) + 4 = 3(q + 1) + 1
	Division by 3	Divisible	Leaves remainder 2 ∴ not divisible	Leaves remainder 1 ∴ not divisible
Case 2:	When n = 3q + 1	3q + 1	(3q + 1) + 2 = 3(q + 1)	(3q + 1) + 4 = 3(q + 1) +2
Case 2:	Division by 3	Leaves remainder 1 ∴ not divisible	divisible	Leaves remainder 2 ∴ not divisible
Case 3:	When n = 3q + 2	3q + 2	(3q + 2) + 2 = 3(q + 1) + 1	(3q + 2) + 4 = 3(q + 2)
Case 3:	Division by 3	leaves remainder 2 ∴not divisible	Leaves remainder 1 ∴ not divisible	divisible

In case 1, n is divisible by 3 but n + 2 and n + 4 are not divisible by 3.

In case 2, n + 2 is divisible by 3 but n and n + 4 are not divisible by 3.

In case 3, n + 4 is divisible by 3 but n and n + 2 are not divisible by 3.

Hence, one and only one out of n, n + 2 or n + 4 is divisible by 3, where n is any positive integer.

FUNDAMENTAL THEOREM OF ARITHMETIC:

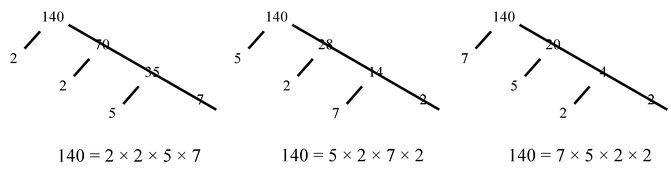
Every composite number can be expressed as a product of primes, and this factorization is unique, except for the order in which the prime factors occur.

By taking the example of prime factorization of 140 in different orders

Real Numbers

SOME IMPORTANT RESULTS :

(i) Let ‘p’ be a prime number and ‘a’ be a positive integer. If ‘p’ divides a2, then ‘p’ divides ‘a’.

(ii) Let x be a rational number whose decimal expansion terminates. Then, x can be expressed in the form p/q where p and q are co-primes, and prime factorization of q is of the form 2m × 5n, where m, n are non-negative integers.

(iii) Let x = p/q be a rational number, such that the prime factorization of q is not of the form 2m × 5n where m, n are non - negative integers. Then, x has a decimal expansion which is non - terminating repeating.

1. Is 7 × 11 × 13 + 11 a composite number?

Sol. 11 x (7 x 13 + 1) = 11(91 + 1)= 11 × 92 = 1012

It is a composite number which can be factorized into primes.

2. Find the LCM and HCF of 84, 90 and 120 by applying the prime factorization method.

Sol. 84 = 22 × 3 × 7, 90 = 2 × 32 × and 120 = 23 × 3 × 5

Prime factors	Least exponent
2	1
3	1
5	0
7	0

∴ HCF = 21 × 31 = 6.

Common prime factors	Greatest exponent
2	3
3	2
5	1
7	1

∴ LCM = 23 × 33 × 51 × 71

= 8 × 9 × 5 × 7

= 2520.

3. Given that HCF (306, 657) = 9. Find the LCM (306, 657).

Sol. HCF (306, 657) × LCM (306, 657) = 306 × 657

⇒ 9 × LCM (306, 657) = 306 × 657

⇒ LCM (306, 657) = 306 x 657/9 = 34 x 657

⇒ LCM (306, 657) = 22338

4. Prove that √2 is an irrational number.

Sol. Let assume on the contrary that √2 is a rational number.

Then, there exists positive integer a and b such that

√2 = a/b where, a and b are co primes i.e. their HCF is 1.

⇒ (√2)² = (a/b)²

⇒ 2 = a²/b²

⇒ a² = 2b²

⇒ a² is multiple of 2

a is a multiple of 2 ....(i)

⇒ a = 2c for some integer c.

⇒ a² = 4c²

⇒ 2b² = 4c²

⇒ b² = 2c²

⇒ b² is a multiple of 2

b is a multiple of 2 ....(ii)

From (i) and (ii), a and b have at least 2 as a common factor. But this contradicts the fact that a and b are co-prime. This means that √2 is an irrational number.