
Angles: Angles are an important part of shapes and geometry. They are formed when two lines meet at a point. Angles are all around us, like in the corners of a book, the hands of a clock, or the edges of a road sign.
Angles are not only useful in math but also in real-life designs and structures, making them an interesting and important concept to study.
Understanding angles helps us learn how shapes are made and how they fit together. In this topic, we will learn about the parts of angles, how to measure an angle, and how to construct angles. Angles are fun to learn and are used in many everyday things we see and use.
Also Check: Geometry
About CuriousJr Mental Maths Classes
At CuriousJr , part of Physics Wallah, we provide specialized Mental Maths Classes that help students master problem-solving skills. With over 50 mental math strategies our program is designed to enhance both speed and accuracy in calculations. Our classes focus on developing logical reasoning and critical thinking skills enabling students to tackle complex problems effortlessly. By participating in our CuriousJr classes, you will not only improve your ability to solve challenging tasks but also strengthen your overall cognitive abilities. This empowers you to achieve more in less time making learning math an enjoyable and rewarding experience.What is an Angles in Maths?
An angle in mathematics is formed when two straight lines meet at a point, known as the vertex . Imagine two lines extending from the same point, creating a space between them. This space is called an angle (∠).
Angles are measured in degrees, and a full circle has 360 degrees. The size of the angle tells us how wide or narrow the space is. Smaller angles have a smaller space between the lines, while larger angles have a bigger space.
Angles are important in geometry because they help us understand how lines and shapes are connected. They are used in many areas of life, like designing buildings, drawing shapes, or reading clocks.
Also Read: AM and PM
Parts of Angles
The following are the main parts of an angle:
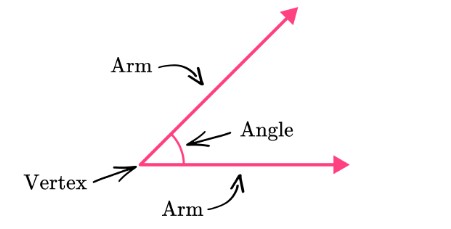
- Vertex: The vertex is the point where the two rays of an angle meet. It’s the starting point from which we measure the angle. For example, in angle ∠ABC, point B is the vertex.
- Rays (or Arms): The rays are the two lines that form the angle. They start at the vertex and go on forever in opposite directions. In angle ∠ABC, the rays are lines AB and BC.
- Angle Measure: The angle measure tells us how much the two rays have turned. It’s usually measured in degrees or radians. A protractor is often used to measure angles in degrees.
- Interior of the Angle: The interior is the space between the two rays. It’s the smaller area the rays enclose. In angle ∠ABC, the interior is the space between rays AB and BC.
- Exterior of the Angle: The exterior is the space outside the angle. It’s the larger area beyond the rays. In angle ∠ABC, the exterior is the space outside of rays AB and BC.
Also Check: Pie Chart
Types of Angles
An angle is formed when two rays meet at a point called the vertex and is measured in degrees. Angles are classified based on size, rotation, position, and their relationships in geometry.
Types of Angles Based on Measurement
Angles are classified based on how wide or narrow they open. Each type has a different degree of measurement and is used in various shapes and designs.
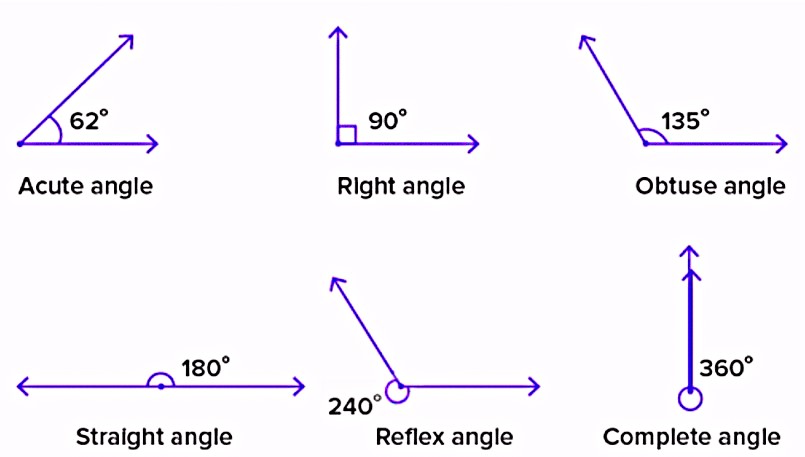
- Acute Angle: An acute angle measures less than 90 degrees. These angles are small and sharp, typically found in triangles and other shapes that have pointed corners.
- Right Angle: A right angle measures exactly 90 degrees. It forms a perfect "L" shape, which is commonly seen in squares, rectangles, and other shapes.
- Obtuse Angle: An obtuse angle is an angle that measures greater than 90 degrees but less than 180 degrees. Obtuse angles are wider than right angles.
- Straight Angle: A straight angle measures exactly 180 degrees. It forms a straight line, dividing the space into two equal parts.
- Reflex Angle: A reflex angle is an angle that measures greater than 180 degrees but less than 360 degrees. Reflex angles are larger than straight angles, as they extend beyond a straight line.
- Complete Angle: A complete angle is an angle that measures 360 degrees. A complete angle can be represented by a circle or a point with an arrow indicating a full rotation.
Types of Angles Based on Rotations
Angles can also be classified by the direction in which they are measured. This classification helps in understanding rotations and angle movements in geometry.
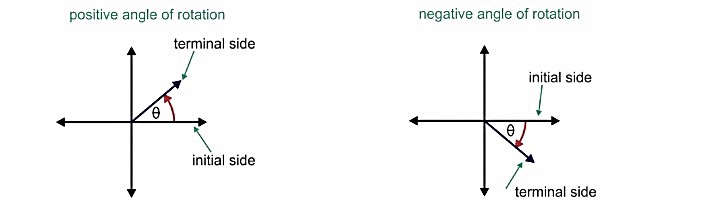
- Positive Angle: A positive angle is measured counterclockwise from the initial side to the terminal side. This type of angle is commonly used in geometry and represents rotation in the counterclockwise direction. Positive angles are frequently encountered in basic trigonometry and geometry.
- Negative Angle: A negative angle is measured clockwise from the initial side to the terminal side. Negative angles represent rotations in the opposite direction.
Types of Angles Based on Position
Angles can be related to each other by position. These relationships help in solving problems in geometry.
- Adjacent Angles: Adjacent angles share a common vertex and side but do not overlap. These angles are used in various geometric proofs and constructions to show the relationships between angles formed by intersecting lines.
- Complementary Angles: When the sum of two angles is 90 degrees, they are called complementary angles. These angles frequently appear in right triangles and are employed in geometric patterns to create right angles.
- Supplementary Angles: When the sum of two angles equals 180 degrees, they are considered supplementary. These angles are commonly found in straight-line constructions and contribute to our understanding of linear pairs of angles.

Types of Angle Pairs
When two lines intersect, different types of angle pairs are formed. These angle pairs have specific relationships and properties.
- Vertical Angles: When two lines cross, they form vertical angles, which are pairs of angles that are opposite each other. These angles are always equal in size and are essential for understanding how intersecting lines relate to one another in geometry.
- Alternate Interior Angles: Alternate interior angles are located on opposite sides of a transversal and between two parallel lines. These angles are equal when the lines are parallel, making them useful for proving geometric properties and solving problems with parallel lines.
- Corresponding Angles: Corresponding angles are found at matching corners when a transversal crosses two lines. These angles are equal when the lines are parallel, and they are important for understanding the relationship between parallel lines and transversals in geometry.
Interior and Exterior Angles
In polygons, interior and exterior angles play an important role in understanding the shape and size. They help define the properties of the polygon.
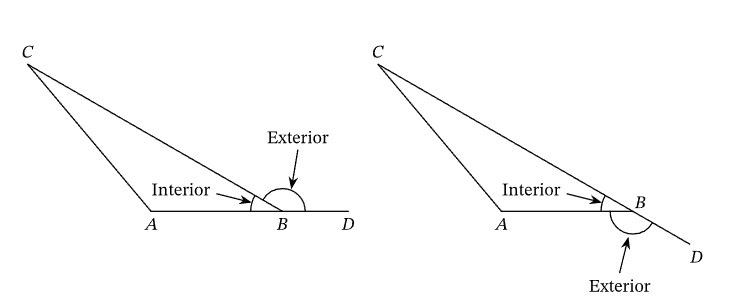
- Interior Angles: Interior angles are the angles inside a polygon. The sum of these angles depends on the number of sides in the polygon. For example, the sum of the interior angles of a triangle is always 180 degrees, and for a quadrilateral, it is 360 degrees.
- Exterior Angles: Exterior angles are formed outside a polygon when one side is extended. The sum of the exterior angles of any polygon is always 360 degrees, no matter how many sides the polygon has.
How to Measure an Angle?
An angle is a shape formed by two lines (called rays) that meet at a common point, called the vertex. Angles are measured in degrees (°), and we use a tool called a protractor to measure them.
Steps to Measure an Angle Using a Protractor:
- Place the Protractor
- Position the protractor so that its center point is on the vertex of the angle.
- Align one side of the angle with the zero-degree line on the protractor.
- Read the Measurement
- Look at where the other side of the angle crosses the protractor’s scale.
- Note the degree number at this point.
How to Construct Angles?
Constructing angles is an important skill in geometry. It involves creating angles with specific measurements using basic tools like a compass. Here are two common methods to do this:
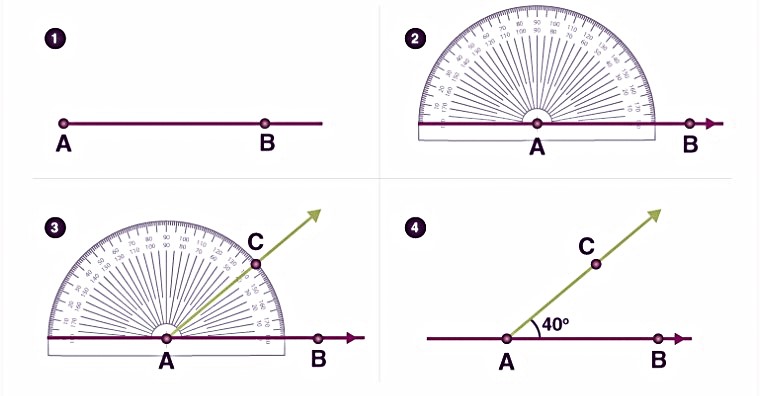
Method 1: Using a Protractor A protractor is a tool used to measure angles in degrees. To make an angle with a protractor, follow these steps:
- Draw a Ray : Use a straightedge to draw a ray, which is a line that goes on forever in one direction. This will be one side of your angle.
- Place the Protractor : Put the center of the protractor at the endpoint of the ray (the vertex of the angle). Align the zero-degree mark with the ray.
- Mark the Desired Angle : Find the angle you want to make on the protractor and mark a point on the paper at this angle.
- Draw the Second Ray : Remove the protractor and draw the second ray from the vertex to the marked point. This completes the angle.
Method 2: Using a Compass A compass is a tool used to draw circles and arcs. You can use it to make angles like 60°, 90°, or 120°, then combine them to create other angles.
Constructing a 60-Degree Angle :
- Draw a Ray : Draw a ray to be the base of your angle.
- Create an Arc : Place the compass point at the endpoint of the ray and draw an arc that crosses the ray.
- Mark the Arc : Without changing the compass width, move it to the point where the arc meets the ray and draw another arc.
- Draw the Second Ray : Draw a ray from the endpoint of the first ray through the point where the arcs meet. This creates a 60-degree angle.
Constructing Other Angles : After making a 60-degree angle, you can split it to make smaller angles (like 30°), or combine angles like 60° and 90° to make angles such as 120° or 150°.
Additional Tips :
- Practice : The more you practice, the better you'll become at constructing angles.
- Use a Sharp Pencil : A sharp pencil will help make clean, precise marks.
- Draw Clear Lines : Keep your lines thin and clear so they don’t confuse you.
- Check Your Work : Use a protractor to check if your angle is correct.
Angles FAQs
What are angles in maths?
What is your definition of an angle?
What are 7 types of angles?
What is a right angle?
What is an acute angle?









