What is Area of a Square? Formulas, How to Find, Derivation, Examples
The area of a square is defined as the space enclosed within its four equal sides. Check out the area of a square formula, its derivation, and solved examples here.
Chandni 22 Aug, 2025
Share
Area of a Square represents the total space it covers within its four equal sides. This concept is not just a part of geometry but a practical tool we encounter in daily life.
Whether it's figuring out how many tiles you need for your floor or determining the size of a garden plot, the area helps us measure and utilize space efficiently.
By learning to calculate the area, we can solve everyday problems effortlessly. In this article, we will explore the concept of the area of a square, including practical examples, formula of area of square, steps to calculate the area of a square using side and diagonal formulas, and its units.
Square in Math
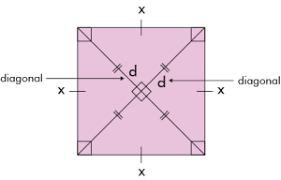
A square is a two-dimensional shape that belongs to the family of quadrilaterals. It is defined by four sides of equal length, with each interior angle measuring 90°.
The opposite sides of the square are parallel to each other. One of its unique properties lies in its diagonals, which are equal in length and intersect at right angles.
This symmetrical and balanced shape is found in many objects that we use in everyday life, such as tiles, photo frames, chessboards, tabletops, and more.
Properties of Square
Here are some common properties of a square:- A square has four sides and four vertices, making it a type of quadrilateral.
- All sides are of equal length, and opposite sides are parallel.
- Each interior angle measures 90°, and the sum of all interior angles is 360°.
- The diagonals are equal in length, bisect each other at 90°, and divide the square into two congruent triangles.
What is the Area of a Square?
The area of a square refers to the amount of flat space enclosed within its four equal sides. In other words, it helps measure how much surface a square-shaped object occupies. For example, think of a square garden. The area of the garden represents the total space available within its boundaries for planting grass, flowers, or other decorations. The unit of measurement for area is always in square units, such as square meters, square centimeters, or square feet.
What is the formula of area of square
The area of a square is expressed as the number of square units required to fill the square. Area is often defined as the space within the boundaries of a two-dimensional figure or flat object. Using square meters (m2) as the standard unit, the measurement is performed in square units. Now lets find the area of a square:
Area of square = Side × Side (square units)
Area of a Square Formula
The area of square formula helps calculate the space enclosed within its four equal sides. It is expressed as: Area of square = Side × Side (square units) If the diagonal of the square is given, the area of a square formula becomes: Area = (Diagonal²) ÷ 2 (square units)Example 1: Using the Side
Let’s consider a square garden with each side measuring 8 feet. Using the formula: Area = Side × Side = 8 × 8 = 64 square feet. The garden occupies a total area of 64 square feet.Example 2: Using the Diagonal
For a square photo frame with a diagonal of 10 inches: Area = (Diagonal²) ÷ 2 = (10 × 10) ÷ 2 = 100 ÷ 2 = 50 square inches.Area of Square Formula Using Diagonal Derivation
The formula for finding the area of a square using its diagonal can be derived using the Pythagoras theorem. Let the side of the square be "a" units and the diagonal be "d" units. The diagonal divides the square into two equal right-angled triangles. In each triangle, the diagonal is the hypotenuse, and the two sides are the base and perpendicular.Area of a Square Solved Examples
Example 1: Find the area of a square if the length of the diagonal is 14 cm.First, find the area of the playground:
Area = Side² Area = 25 × 25 = 625mNow, calculate the total cost:
Total Cost = Area × Cost per square meter
Total Cost = 625 × 15 = $9375 The total cost to lay grass in the square playground is $9375.Find the area of the hall:
Area of hall = Side² = 50 × 50 = 2500m²Find the area of one tile:
Area of one tile = Side² = 5 × 5 = 25 m²Now, calculate the number of tiles needed:
Number of tiles = (Area of hall) ÷ (Area of one tile) Number of tiles = 2500 ÷ 25 = 100 The total number of tiles required is 100.Find the side length:
Side = Perimeter ÷ 4 = 60 ÷ 4 = 15 cmFind the area:
Area = Side² = 15×15 = 225 cm ² Calculate the total cost: Total Cost = Area × Cost per square cm Total Cost = 225 × 3 = $675 The cost to paint the square is $675. Join Online Tuition Class Now!!| Related Articles | |
| Area of Rectangle | Isosceles Triangle |
| Composite Numbers | Differentiation |
| Perimeter of Rectangle | Surface Area of Cylinder |
Area of a Square FAQs
How is the area of a square different from the perimeter?
The area measures the total space inside the square, while the perimeter measures the total length of all four sides.
Area = Side × Side
Perimeter = 4 × Side
Can the area of a square be negative?
No, the area of a square cannot be negative because it represents the physical space covered, which is always a positive value.
Why is the area of a square measured in square units?
The area of a square is measured in square units because it represents the number of small square units that fit inside the square, such as square meters (m²) or square centimeters (cm²).
How can I visually understand the area of a square?
Imagine a square floor where each side is divided into smaller 1 cm squares. The area is the total number of these smaller squares that fit inside the larger square.
What happens to the area of a square if its side is doubled?
If the side of a square is doubled, the area becomes four times larger. For example, if the side is 5 cm (area = 25 cm²), doubling it to 10 cm results in an area of 100 cm².
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.