Circumference of a Circle: Meaning, Formulas, and Solved Examples
Chandni 6 Aug, 2025
Share
The Circumference of a circle is an important mathematical concept that is useful and relevant in practical scenarios as well. You start running along a circular track and come to the point where you started; it means you have covered a distance equal to the circumference of a circle.
In other words, it is the length of the boundary surrounding a circle. Understanding the concept and calculation process for the Circumference of circle formula helps in a quick solution to practical-based mathematical problems. In this article, we will discuss different aspects of the circumference of a circle, including its definition, formula, and calculation methods, as well as solved examples.Read More - Radius of a Circle
What is the Circumference of a Circle?
The circle is a round geometrical shape where each point on its boundary is at equal distance from a fixed point called the circle's center. The circumference of a circle refers to the measurement of the length of its boundary. We can say that it is the outline of the circle. The circumference is expressed in the unit that measures the length, such as centimeters, meters, kilometers, etc.
Circumference and Perimeter: Are they the same?
The perimeter of any closed geometrical shape is defined as the total length of the boundary or outline surrounding the shape. In that sense, the circumference is the perimeter of a circular shape. However, in geometry, a unique name is given to the perimeter of a circle, which is the circumference.
Elements that Make Up the Circle Circumference
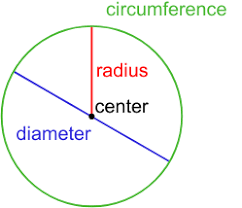
A circumference is formed when we have a fixed point and draw the path of all points equidistant from this fixed point, creating a circular shape in a two-dimensional plane.
The distance between the fixed point, or center, and any point on the boundary of the circle is the radius of the circle. The circle’s diameter is the straight line through the center, touching the Circumference at both ends.
How To Find the Circumference of a Circle?
Find the circumference of the circle is not the same as finding the perimeter of any other geometrical shape. The perimeter of polygons, which are shapes enclosed by multiple sides, can be calculated by finding the total length of all sides. However, the circle is a curved figure, so calculating its perimeter or boundary requires a different method.
To find the circumference of a circle, we require the radius of the circle. Then, we double the circle's radius, which gives the diameter. We then multiply the diameter by a mathematical constant called Pi (denoted as π), and get the circle's circumference.
The constant Pi has an approximate value of 3.14159… which doesn't give an exact value. So, for calculation purposes, we take the value of Pi as 22/7.
Circle Circumference Formula
The circumference of a circle is 2πr formula. We can write the Circle circumference formula as follows:
Circumference C = 2πr
Here, r is the radius of the circle.For example, if the radius of a circle is 20 cm, we can find the Circumference using the above formula (we take the value of π =3.14)
Solution:
Radius = 20 cm We put the value of r (radius) in the circumference formula, C = 2 × π × 20 cm C = 2 × 3.14 × 20 cm = 125.6 cm Therefore, the Circumference of a circle with a radius of 20 cm is 125.6 cm.The Ratio of Circumference to Diameter
From the above Formula of circumference of circle, the circumference ratio to the diameter gives the value of Pi. π = C/2r Therefore, the Pi (π) can be defined as the ratio of the circumference and diameter of a circle.The Perimeter of a Semi- C ircle
A semicircle is the half of a circle. A curved line and a straight line enclose it. The curved line measures half of the circle's Circumference, and the straight line measures the circle's diameter. So, the formula for the circumference of a semicircle can be written as follows: Perimeter of semi-circle = πr + 2r Where r is the radius of the circle.Circumference of a Circle Important Points
- Circumference is the perimeter of a circular shape that represents the length of its boundary.
- The circle’s circumference calculation uses a mathematical constant π(Pi) which approximated as π = 22/7 or 3.14
- The circumference of a circle is determined using the radius, or diameter.
- The circumference of a circle increases as the diameter increases, and vice versa.
Circumference of a Circle Solved Examples
1. If the radius of a circle is 35 cm, find the circumference of the circle.
Solution:
We will use the circumference formula: 2πr = 2 × 22/7 × 35 = 220 cm. Therefore, the Circumference of the circle is 220 cm.2. If the circumference of a circle is 660 cm, find its radius and diameter.
Solution:
Circumference of the circle = 660 cm Taking the radius of the circle = r cm, we get: 660 = 2πr Or, 660 = 2 × (22/7) × r Or, r = 660 x 7/44 Or, r = 105 Diameter = 2r = 2 × 105 = 210 Therefore, the radius is 105 cm, and the Diameter is 210 cm. 3. An athlete takes six rounds on a circular track with a diameter of 56 meters. What is the total distance covered by the athlete?Solution:
One complete round of the circular track means covering a distance equal to the perimeter of the circular track. So, in one round, the athlete covers a distance of 22/7 x 56 = 176 meters. Therefore, for six rounds, the athlete covers a distance of 176 x 6, which is equal to 1056 meters or 1.056 km.4. A wire forms a square shape with each side of 11 cm. If the same wire is used to create a circle, what will be the radius of the circle?
Solution:
The exact length of the wire is used to form the square and the circle. So, the square's perimeter and the circle's circumference will be the same. The perimeter of the circle with each side of 11 cm can be calculated as: Perimeter of square = 4 x 11 = 44 cm Therefore, the Circumference of the circle will be 44 cm. Let's take the radius of the circle as r cm. Substituting the value in the circumference formula, we get: 44 = 2 x 22/7 x r Or, r = 7 So, the radius of the circle formed is 7 cm. Join Online Tuition Class for Kids Now!!| Related Articles | |
| Area of Rectangle | Isosceles Triangle |
| Composite Numbers | Differentiation |
| Perimeter of Rectangle | Surface Area of Cylinder |
Circumference of a Circle FAQs
Why is it not easy to measure the circumference of a circle with a scale?
Why is Pi (π) used in the formula for circumference?
What value of Pi is considered in case a decimal value of circle circumference is required?
Are perimeter and circumference synonymous?
How does the circumference change when the radius is doubled?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
