Equivalent Fractions: Definition, How to Calculate, and Examples

Equivalent fractions are fraction numbers that represent the same portions when compared to a whole quantity. We write them differently, but they denote the same thing. Eating 1 part of a pizza from 4 equal parts is the same as having 2 pieces from a pizza cut into 8 equal parts. That’s the concept of equivalent fractions. 

Similarly, adding 1 part of an ingredient to 4 parts of another is equivalent to 2/8. Understanding equivalent fractions helps you compare, calculate, and simplify fractions more easily in everyday tasks. This article explains equivalent fractions with examples to help clarify your concept of the application of equivalent fractions.  

Read more - Fraction Questions for Class 5

What is an Equivalent Fraction?

The definition of equivalent fractions indicates that these fractions have the same value, but each of their numerators and denominators is different from the other. As we simplify these fractions, we get the same result at each step.

For example, 3/15, 9/45, 12/60, and 6/30 are equivalent fractions because each of these fractions gives a value of 1/5 on simplification.

Enroll Now for Kids Online Classes

How to Find Equivalent Fractions?

Finding equivalent fractions makes mathematical calculations simpler and easier. Let’s look at some simple methods to do the same.

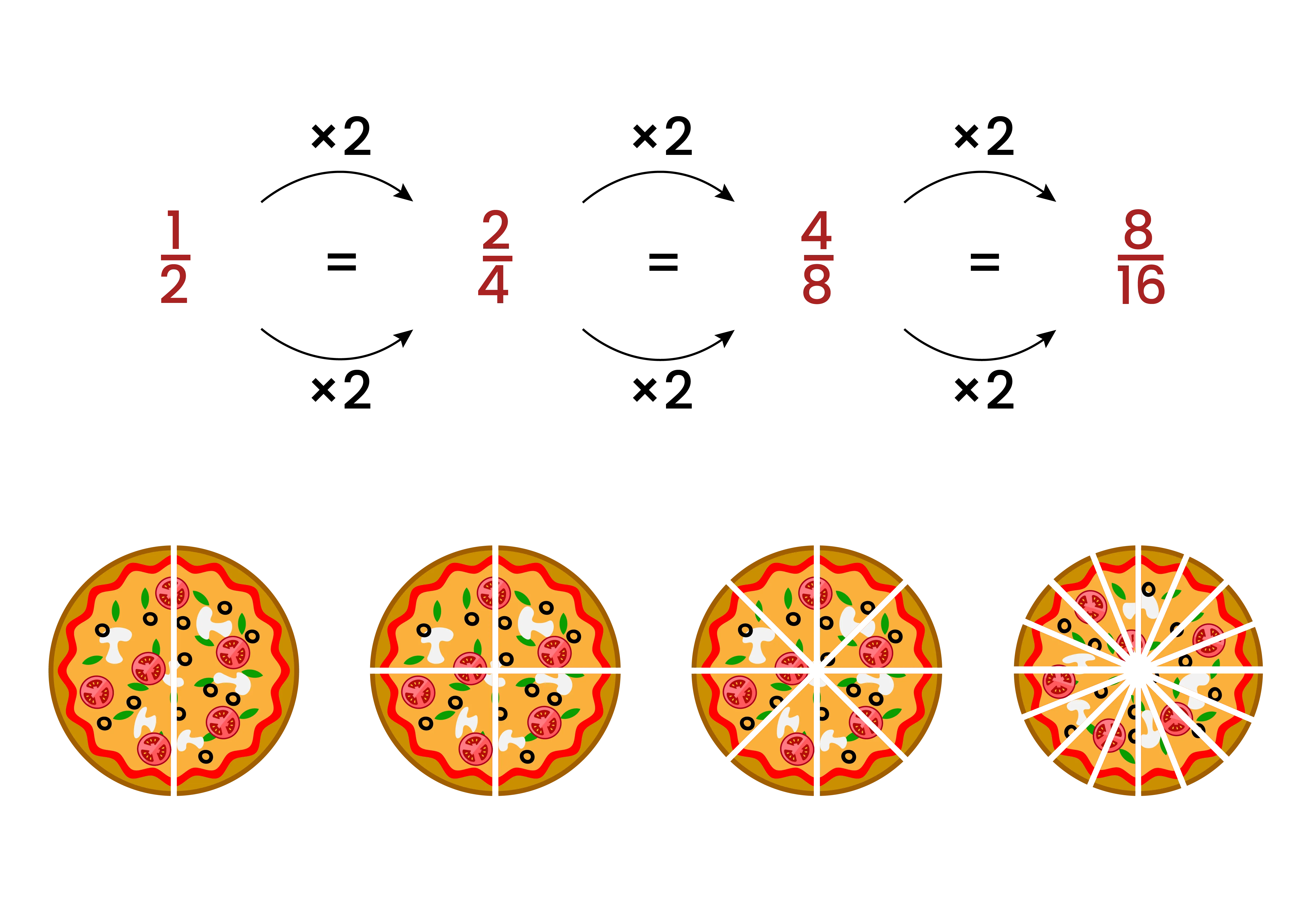
Multiplying The Numerator and The Denominator by The Same Number

The easiest method to find the equivalent fraction of a given fraction is to multiply its numerator and denominator by the same number.

For example, there is a fraction 2/5, and we have to find the equivalent fractions.

We can multiply 2 (the numerator) and 5 (the denominator) by the same number, say 3.

Then we get, 2/5 = (2 x 3)/ (5 x 3) = 6/15

Again, by multiplying both 2 and 5 by 4, we get 2/5 = (2 x 4)/ (5 x 4) = 8/20

Similarly, by multiplying both 2 and 5 by 7, we get 2/3 = (2 x 7)/ (5 x 7) = 14/35

Therefore, 2/5, 6/15, 8/20, and 14/35 are equivalent fractions.

Read More - Multiplication

Dividing The Numerator and The Denominator by The Same Number

Another way to find the equivalent fractions is by dividing the numerator and denominator by the same common factor. This will simplify the fraction to a lower form.

For example, we need to find equivalent fractions of the given fraction 160/240.

First, we have to find the lowest common factor of 160 and 240, which is 2.

By dividing both 128 and 240 by 2, we get 160/240 = 160÷2/240÷2 = 80/120

Again, a common factor of 80 and 120 is 5, so we divide 80 and 120 by 5.

We get 80/120 = 80÷5/120÷5 = 16/24

Again, by dividing both 16 and 24 by their common factor 4, we get,

16/24 = 16÷4/24÷4 = 4/6

Further, we simplify 4/6 by dividing the numerator and denominator by 2.

Thus, we get 4/6 = 4÷2/6÷2 = 2/3

So, the equivalent fractions of 160/240 are 80/120, 16/24, 4/6, and 2/3. 

Read More - Co-prime Numbers

How To Determine if Two Fractions are Equivalent?

To determine whether two fractions are equivalent, we employ some useful methods as explained below.

Making the Denominators the Same

When two fractions are given, we must make their denominators the same: the LCM (Lowest Common Multiple) of both denominators. This is done by multiplying the numerator and denominator by a suitable number such that both denominators become equal to the LCM.

Let’s consider two fractions, 4/16 and 6/24. The LCM of 16 and 24 is 48. So, we have to make the denominator of both fractions 24. This can be done as follows:

4/16 = (4 x 3)/ (16 x 3) = 12/48

And 6/24 = (6 x 2)/ (24 x 2) = 12/48

We observe that the values of both fractions are the same. So, they are equivalent fractions.

Read More - Equation

Finding the Decimal Values of Both Fractions

We can find the decimal values of both fractions by actual divisions. So, for the fractions 4/16 and 6/24, we get the decimal values as follows:

4/16 = 0.25

6/24 = 0.25

Since the decimal values of both fractions are the same, they are equivalent fractions.

Cross Multiplication Method

Cross multiplication is another easy method to determine whether two fractions are equivalent. It means the numerator of one fraction is multiplied by the denominator of the other fraction. If the products are found equal, then the fractions are equivalent.

For example, let’s take two fractions, 3/5 and 9/15. By cross multiplication, we get,

3 x 15 = 45

5 x 9 = 45

Here, both products give equal values. So, 3/5 and 9/15 are equivalent fractions.

Read More - Addition and Subtraction of Decimals Examples

Visual Representation of Equivalent Fractions

As per the equivalent fraction definition, they denote the same portions as a part of the whole. We can represent this concept pictorially by making divisions in a shape equivalent to the denominator and shading the portions denoted by the numerator. This is explained in the image given below.

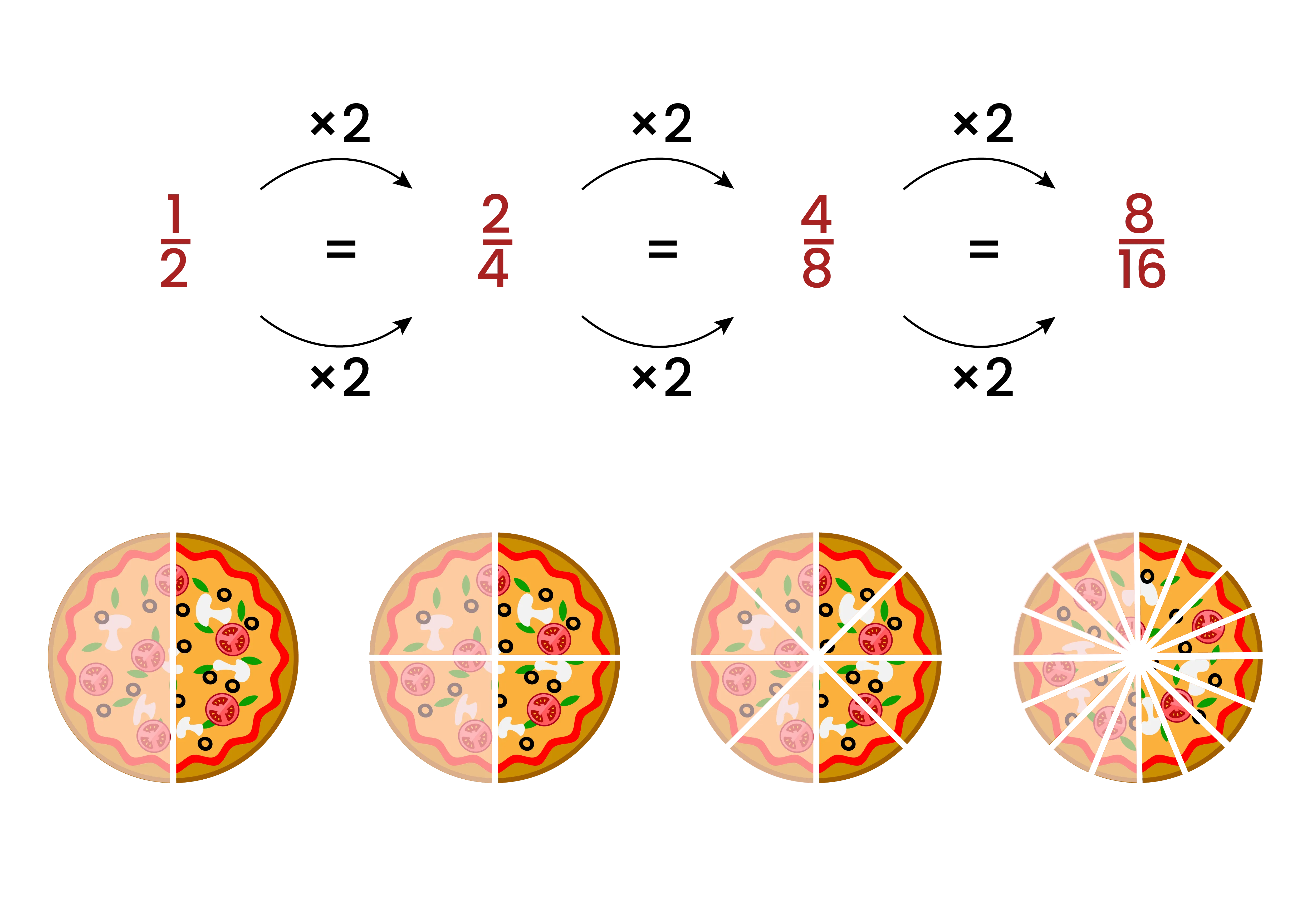
This visual representation also helps determine whether two or more fractions are equivalent or not.

Read More - International Numeral System

Solved Examples

1. Are 32/40 and 27/36 equivalent fractions?

Solution:

By simplifying both fractions, we get

32/40 = 4/5 and 27/36 =3 /4

Now, the LCM of 5 and 4 is 20. So, we can write:

4/5 = (4 x 4)/ (5 x 4) = 16/20

And 3 /4 = (3 x 5)/ (4 x 5) = 15/20

We find that the values of both fractions are not the same. So, 32/40 and 27/36 are not equivalent fractions.

2. If 5/14 and p/42 are equivalent fractions, find the value of p.

Solution:

Given that 5/14 = p/42

Therefore, by cross multiplication, we get 14 x p = 5 x 42

Or, p = (5 x 42)/14 = 5 x 3 = 15

Ans. The value of p is 15.

3. Give two equivalent fractions of 24/42 by the simplification method.

Solution:

The given fraction is 24/42.

Dividing both the numerator and denominator by the common factor 2, we get:

24/42 = 12/21

Again, by dividing 12 and 21 by their common factor 3, we get:

12/21 = 4/7

So, the two equivalent fractions of 24/42 are 12/21 and 4/7.

4. Check whether 5/9 and 25/45 are equivalent fractions using the cross-multiplication method.

Solution:

By cross multiplication of the given fractions, we get:

5 x 45 = 225 and 25 x 9 = 225

Both these products are equal.

So, the fractions 5/9 and 25/45 are equivalent fractions. 

Make math easier and more fun for your child with CuriousJr Kids Online Classes. Our friendly and engaging teachers simplify mathematics topics like equivalent fractions, multiplication, division, and more through interactive lessons and visual examples. Enroll your child today to enhance their confidence and strengthen problem-solving skills from home.