
Suppose you are asked to draw a line on a blank page. What comes to mind? If you think of something slanted, like a roof, you might draw a diagonal line.
If you picture something tall, like a tree, you’d likely draw a vertical line running up and down. But if you imagine something flat, like a bookshelf or a calm river, you’d naturally draw a horizontal line stretching from left to right.
A horizontal line is a straight line that stays at the same height without tilting. It has a slope of zero, meaning there’s no vertical change as it extends.
In the coordinate plane, horizontal lines run parallel to the x-axis and cross the y-axis at a single fixed point. Let’s understand more about what is horizontal line, see a horizontal line example, learn about the horizontal line slope, and how to draw a horizontal line step-by-step.
Check Out - Equation: Definition, Types, Examples, Differences
What is a Horizontal Line?
We observe horizontal lines in everyday objects, shapes, and designs. Examples include tabletops, bookshelves, and the base of a staircase. In mathematics, horizontal lines are integral to the structure of many 2D and 3D shapes, such as squares, rectangles, trapezoids, and cubes.
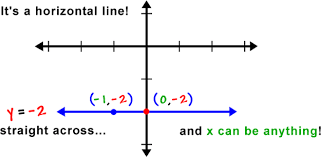
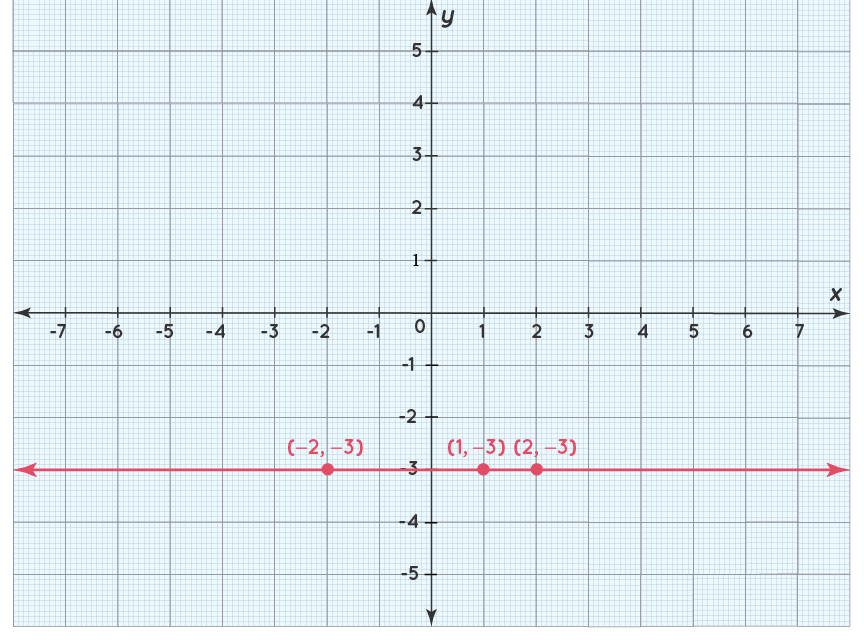
On a coordinate plane, a horizontal line is parallel to the x-axis. If two points on the line share the same y-coordinate, the line is considered horizontal. For example, a line passing through points (-1,-2) and (0,-2) is horizontal because the y-coordinate remains constant at -2.
Another interesting property of horizontal lines is that they are always perpendicular to vertical lines, which go up and down. This relationship is fundamental in geometry and forms the basis of many designs and patterns we observe in both nature and human-made structures.
We see horizontal lines everywhere. A table, the edge of your book, or the bottom of a chalkboard are all horizontal line examples. These are great ways to understand what is horizontal line.
Horizontal Line Meaning in Geometry
The horizontal line meaning in geometry is simple: it is a line that runs left to right, parallel to the x-axis. It never goes up or down. If you see a line that stays flat, you already understand what is horizontal line.
In a graph, when you plot a horizontal straight line, you will see that it touches different x-values but has the same y-value.
Another horizontal line example is y = 2. This line goes through (1, 2), (3, 2), and (10, 2). The y-coordinate is 2 for every point, so it is a horizontal straight line.
Check Out - Cuboid: Definition, Shape, Properties, Formulas, and Examples
Slope of Horizontal Line
Let’s talk about horizontal line slope.
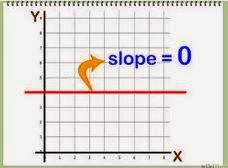
The slope of a horizontal line is zero because there is no vertical change (or rise) as you move along the line.
Here's a fun way to remember: If you are walking on a horizontal line, you don’t go up or down. You walk flat. That’s why the horizontal line slope is 0.
To calculate the slope, we use the formula:
Slope = Rise/Run or
Slope = Change in y-coordinate/Change in x-coordinate
In the case of a horizontal line:
- The y-coordinate remains constant, meaning there is no vertical change (Δy = 0)
- The x-coordinate changes as the line moves left to right (Δx ≠ 0)
Since the numerator (rise or Δy) is zero, the slope becomes: Slope = 0/Run = 0
This zero slope indicates that the line has no inclination and is perfectly flat, parallel to the x-axis.
Horizontal Line Equation
The general equation for a horizontal line in a 2D coordinate system is:
y = mx + cy
Where:
- m is the slope of the line.
- c represents the y-intercept, which is where the line crosses the y-axis.
y = 0x + c
y = c
Here, c is a constant value.
Steps to Draw a Horizontal Line
How to Draw a Horizontal Line? Learning to draw a horizontal line is easy
Steps to draw a horizontal line:
-
Pick a point. For example: (4, 3)
-
Note the y-value. Here, it’s 3.
-
Add more points with the same y-value. Like: (0, 3), (2, 3), (7, 3)
-
Connect them using a ruler. You now draw a horizontal line.
This line will be flat and stretch from left to right. You just created a perfect horizontal straight line.
Try this fun activity: Take your math notebook and draw a horizontal line using your pencil. Label the y-value. It helps you remember the horizontal line meaning.
Real-Life Horizontal Line Examples
Let’s find some more horizontal line examples from everyday life:
-
The edge of your study table
-
The blackboard in your classroom
-
Water in a glass (when not tilted)
-
The line where the sky meets the ocean
Each of these things shows what is horizontal line. These horizontal line examples are easy to see and understand.
Horizontal Line Symmetry
A horizontal line of symmetry divides an object, shape, or letter into two equal halves, with each half mirroring the other. This line runs parallel to the ground or horizon, creating identical sections above and below it.
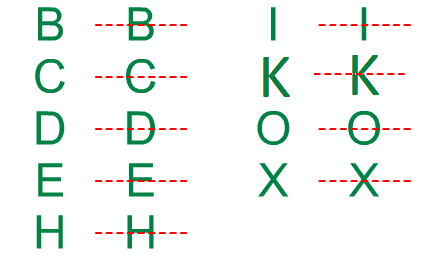
In letters, horizontal symmetry is seen in characters like B, C, D, E, H, I, and O. When a line is drawn across their middle, the upper and lower parts reflect each other perfectly. This property is visually balanced and makes these letters appear the same from a top-down perspective.
Shapes also frequently exhibit horizontal symmetry. A circle split by a horizontal line through its center creates two matching halves. Similarly, a rectangle, when divided horizontally across its center, results in two equal parts.
Squares and some triangles, like isosceles triangles with horizontal bases, demonstrate this as well.
Horizontal symmetry is not just a geometric concept; it’s prevalent in real life too. Nature and design often incorporate this principle. The wings of a butterfly, the reflection of trees on a still lake, or even the layout of certain architectural elements like bridges or floors, highlight the appeal of symmetry.
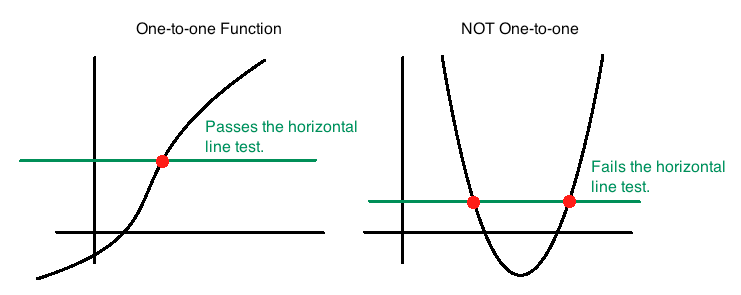
Horizontal Line Test
The horizontal line test is used to check if a function is one-to-one. To perform this test, draw a horizontal line across the graph of the function.
- If the horizontal line intersects the graph at only one point , the function is one-to-one.
- If the horizontal line intersects the graph at more than one point , the function is not one-to-one.
A one-to-one function means that for every unique x, there is a unique y, and vice versa. If a horizontal line cuts the graph more than once, it indicates that the same y value corresponds to multiple x values, which disqualifies the function from being one to one.
This test visually confirms whether a function meets the criteria for one-to-one mapping.
Horizontal Lines in Art and Design
Artists and designers use horizontal lines all the time. They use them to create calm and peaceful images. When you draw a horizontal line in a drawing, it can make the picture feel balanced.
For example, a drawing of the ocean often has a horizontal straight line where the water meets the sky. That is a perfect horizontal line example.
Understanding what is horizontal line helps you become better in art, too!
Differences Between Horizontal Lines and Vertical Lines
Horizontal lines are parallel to the ground or horizon and are often called "sleeping lines." In the Cartesian system, they are parallel to the x-axis, running from left to right.
The slope of a horizontal line is zero, and its equation is represented as y = k, where k is the constant y-coordinate.
E xamples include the base of a figure, a straight road, or the bottom of a staircase.
Vertical lines , on the other hand, are perpendicular to horizontal lines and are known as "standing lines." These lines run up and down in the Cartesian system, parallel to the y-axis.
Their slope is undefined, and their equation is written as x = h, where h is the constant x-coordinate.
Examples of vertical lines include a tall tower, a flagpole, or the height of a building.
Horizontal and vertical lines are perpendicular to each other. While horizontal lines form a 0-degree angle with the horizon, vertical lines form a 90-degree angle. Both types of lines are fundamental in understanding shapes, structures, and spatial orientation.
Horizontal Lines Solved Examples
Find the equation of the horizontal line passing through the point (3,7).
Solution: The slope of a horizontal line is m = 0. Using the point-slope formula:
y − y 1 = m(x−x 1 )
Substitute (x 1 ,y 1 ) = (3,7), and m= 0
y − 7 = 0(x−3) ⟹ y = 7
The equation of the horizontal line is y = 7.
Find the equation of the horizontal line when the y-intercept is 8.
Solution: The equation of a horizontal line is given by:
y = k
where, k is the y-intercept.
Given:
k = 8
Substitute the value:
y = 8
Thus, the equation of the horizontal line with y-intercept 8 is:
y = 8
Example 2: Find the equation of the horizontal line when the y-intercept is −5/2.
Solution: The equation of a horizontal line is:
y = k
where k is the y-intercept.
Given:
k= −5/2
Substitute the value:
y= −5/2y
Multiply both sides of the equation by 2 to remove the fraction:
2y = −5
Rewrite in standard form. The standard form for a line is ax + by + c = 0, though for horizontal lines x-terms are absent. Rewrite:
2y + 5 = 0
Thus, the equation of the horizontal line with y-intercept −5/2 is:
2y + 5 = 0
Join Kids Online Tuition Now !!
| Related Articles | |
| Area of Rectangle | Isosceles Triangle |
| Composite Numbers | Differentiation |
| Perimeter of Rectangle | Surface Area of Cylinder |
Horizontal Line FAQs
How do you identify a horizontal line on a graph?
How do horizontal lines interact with vertical lines?
Are horizontal lines always straight?
What happens when two horizontal lines are compared?
How do you differentiate between horizontal and skewed lines?









