
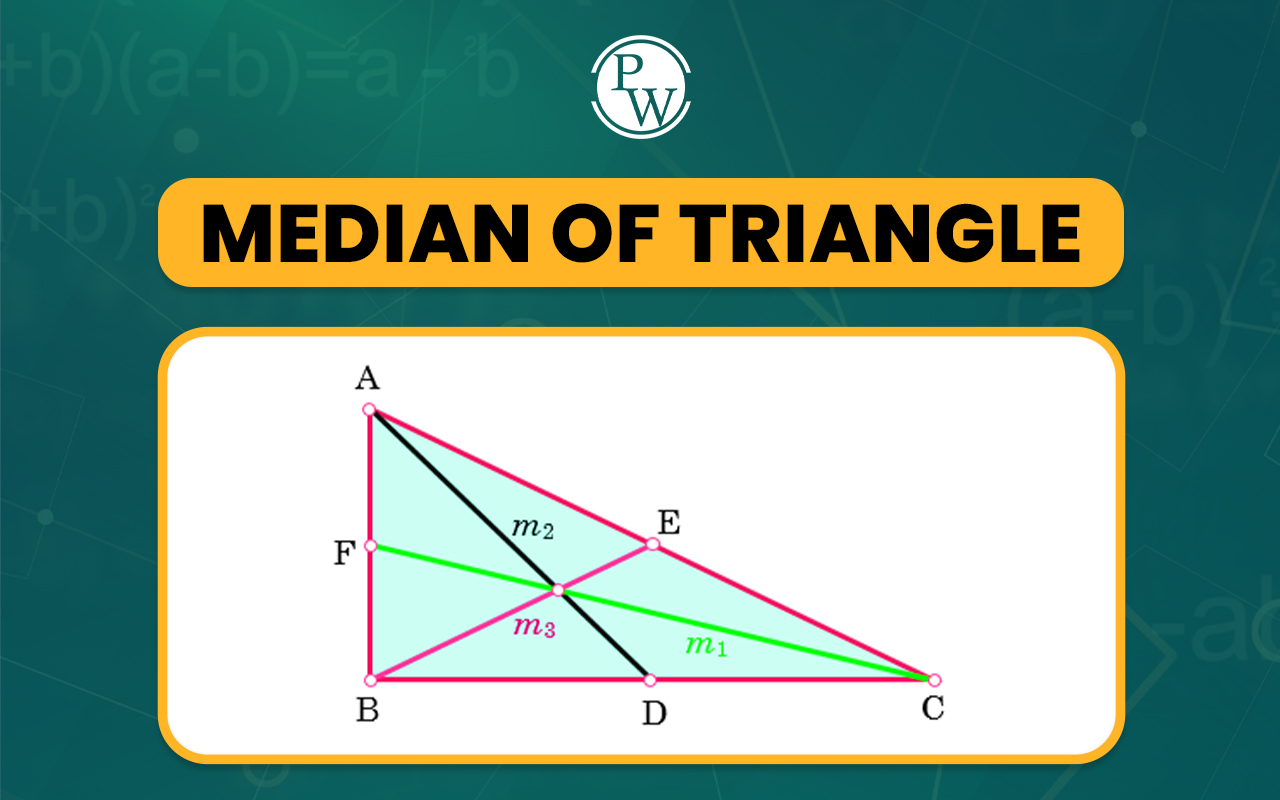
Median of a Triangle: What happens when you draw a line from a vertex of a triangle to the midpoint of the opposite side?
This line, called the median, divides the side into two equal parts. Every triangle has three medians, and they all meet at one point, known as the centroid. The centroid is important because it represents the triangle’s center of balance. In this article, we will explore the median of a triangle in detail, including its properties, steps to find the median of a triangle using coordinates with examples, and more.Median of a Triangle
The median of a triangle is a line segment that connects one corner (vertex) of the triangle to the middle point of the opposite side. Each triangle has three medians, one from each vertex. These medians always meet at a special point inside the triangle called the centroid. The centroid acts like the triangle’s balance point.
What is the Median of a Triangle?
The median of a triangle is a line segment that connects one vertex of the triangle to the midpoint of the opposite side. This means it splits the opposite side into two equal parts. Each triangle has three medians, one from each vertex. Let's understand the concept better with the example below: In the given triangle △ABC A, B, and C are the vertices of the triangle.- D is the midpoint of side BC
- The line segment AD is the median because it connects vertex A to midpoint D, dividing side BC into two equal parts: BD=DC
Median of Triangle Definition
A median of a triangle is a line segment that connects a vertex to the midpoint of the opposite side, splitting the side into two equal parts. Every triangle has three medians, one from each vertex, and they all meet at a single point called the centroid, which is the triangle's center of mass.Median of a Triangle Formula
There is a formula to find the length of a median if you know the lengths of all three sides of a triangle. The formula is: Ma=2b2+2c2−a24. Where a is the side opposite to the median, and b and c are the other two sides. This formula helps calculate how long a median is without measuring it directly.
Length of Median Formula
To find the length of a median, you use the formula based on the triangle’s side lengths. For example, the median from vertex A to the opposite side BC can be found by plugging the side lengths into: Ma=2b2+2c2−a24. This formula comes from a useful rule in geometry called Apollonius’s theorem.
Median of a Triangle Properties
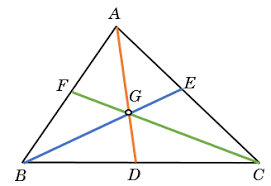
The median of a triangle has unique properties that help explain its geometric significance and balance. Here are the key features:- Each median connects a vertex to the midpoint of the opposite side, dividing that side into two equal parts.
- Every triangle has three medians, one from each vertex, ensuring symmetry across the shape.
- All three medians meet at a single point called the centroid. The centroid is the triangle's center of mass or balance point.
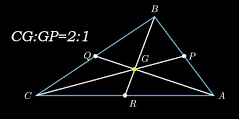
- The centroid divides each median into two parts in a 2:1 ratio. For example, if a median is 9 units long, the segment from the vertex to the centroid is 6 units, and from the centroid to the midpoint is 3 units.
How to Find the Median of a Triangle?
Steps to Find the Median of a Triangle with Coordinates
Step 1: Identify the Coordinates : Begin by noting the coordinates of the triangle's vertices. Denote them as (x 1 ,y 1 ), (x 2 ,y 2 ), and (x 3 ,y 3 )
Step 2: Calculate the midpoint of the opposite side. Choose a vertex for which you want to calculate the median, and identify the opposite side. Use the midpoint formula to find the midpoint of this side.
Midpoint = (x 2 + x 3 /2, y 2 + y 3 /2 )
Step 3: Find the length of the median. With the midpoint determined, use the distance formula to calculate the length of the median from the chosen vertex to the midpoint.d = √(x 1 −Midpoint x ) 2 + (y 1 −Midpoint y ) 2
Step 4: Repeat for the Other Vertices : Repeat the process for the remaining vertices of the triangle to find the medians corresponding to the other two sides.Read More - Perfect Square
Steps to Construct a Median of a Triangle
To construct the median of a triangle, follow these steps:Step 1: Draw the triangle and label its vertices A , B , and C .
Step 2: Find the midpoint of each side by measuring or using the midpoint formula.
Step 3: Connect each midpoint to the opposite vertex using a straight line.
Step 4: Verify that the three lines intersect at a single point, the centroid.
Median of Equilateral Triangle
The median can be drawn in any type of triangle, such as an equilateral, isosceles, or scalene triangle. Each type has unique characteristics related to its medians.Median of a Triangle FAQs
How does the median differ from the altitude in a triangle?
Does a triangle's area depend on its medians?
How do medians help in finding the area of a triangle?
How do medians behave in a right triangle?











