Physics Wallah

Hyperbola: Definition, Equation, Properties, and Examples

A hyperbola is a geometric curve with two symmetrical branches. Explore the derivation of standard and general equations of a hyperbola with solved examples.
authorImageChandni 20 Jan, 2025
Share

Share

Hyperbola

A Hyperbola is a fascinating geometric figure made up of two symmetrical, curved branches that mirror each other. It is created when a plane slices through both halves of a cone at an angle. Unlike circles or ellipses, a hyperbola is an open curve that stretches infinitely.

In this blog, we will explore the parts, properties, equations, and other aspects of a hyperbola to provide a clear understanding of this unique shape.

[video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/Curious-Jr-Ad-3-1-1.mp4"][/video]

What is a Hyperbola?

A hyperbola is the set of all points (locus) where the difference between their distances to two fixed points, called foci, remains constant. This difference is calculated by subtracting the distance to the closer focus from the distance to the farther focus. If P(x,y) is a point on the hyperbola and F and F′ are the two foci, the hyperbola is defined by: ∣PF−PF′∣= 2a Here,
  • PF: The distance from the point P to the first focus F.
  • PF′′: The distance from the point P to the second focus F′.
  • 2a: A fixed constant that defines the shape and size of the hyperbola. It is directly related to the geometry of the curve and helps determine the distance between the two vertices of the hyperbola.
This constant value, 2a, ensures that the hyperbola maintains its unique property at every point on the curve. [video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/curious-jr.mp4"][/video]

Parts of a Hyperbola

A hyperbola has different parts, which are mentioned as follows: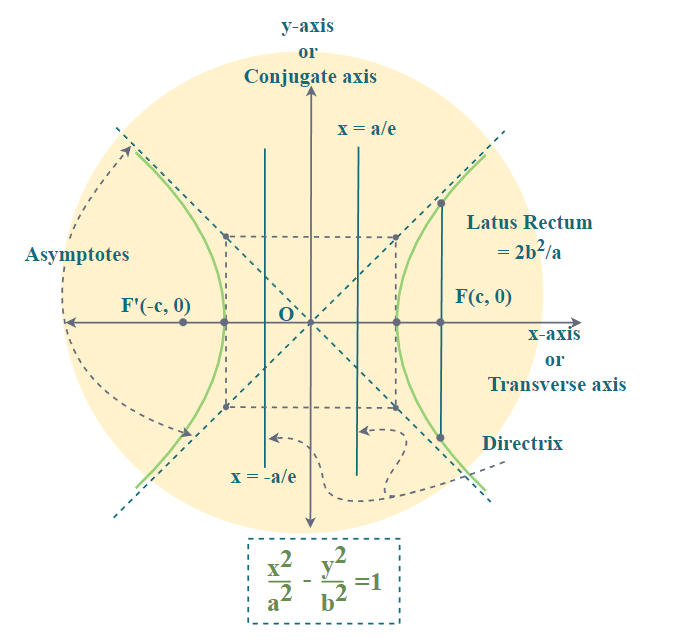 hyperbola
  • Foci : Two fixed points, F(c,0) and F′(−c,0) (horizontal) or F(0,c) and F′(0,−c) (vertical), where c 2 =a 2 +b 2
  • Centre : The midpoint between the two foci, denoted as (h,k) , serving as the hyperbola’s point of symmetry.
  • Major Axis : The axis passing through the vertices and foci, with a total length of 2a.
  • Minor Axis : The axis perpendicular to the major axis, passing through the center, with a total length of 2b .
  • Vertices : Points of intersection of the hyperbola with the major axis, located at (h±a,k) ( horizontal) or (h,k±a) (vertical ).
  • Transverse Axis : A line passing through the center and both foci.
  • Conjugate Axis : A line perpendicular to the transverse axis, passing through the center.
  • Asymptotes : Lines that approach but never touch the hyperbola, defined by y= ±b/ a x
  • Directrix : Fixed straight lines perpendicular to the transverse axis, used to define the hyperbola’s eccentricity.
International Numeral System

Properties of Hyperbola

  • The difference between distances from any point on the hyperbola to its two foci is constant, i.e. ∣PS−PS′∣=2a
  • A hyperbola is rectangular if the transverse and conjugate axes are equal, with eccentricity √2.
  • The latus rectum, a line perpendicular to the transverse axis passing through a focus, has length 2b 2 /a
  • Asymptotes are lines passing through the centre that approach the hyperbola but never intersect it.
  • The auxiliary circle is centered at the hyperbola’s centre with the transverse axis as its diameter, and its equation is x 2 +y 2 =a 2
  • A hyperbola and its conjugate are equal if they have the same latus rectum.

Indian Numeral System

Standard Equations of Hyperbola

The equations of a hyperbola depend on the orientation of its transverse and conjugate axes. The standard forms are as follows: For a hyperbola with the transverse axis along the X-axis : x 2 /a 2 − y 2 b 2 = 1 For a hyperbola with the transverse axis along the Y-axis : y 2 /a 2 − x 2 b 2 =1

Median of a Triangle

Generalized Equations of Hyperbola with Center at (h,k)

When the center of the hyperbola is at (h, k), the equations adjust as follows: For the transverse axis along the x-axis : (x−h) 2 / a 2 −(y−k) 2 /b 2 = 1 For the transverse axis along the y-axis : (y−k) 2 /a 2 −(x−h) 2 b 2 =1 Here,
  • a 2 : Denotes the square of the semi-major axis.
  • b 2 : Denotes the square of the semi-minor axis.
  • h,k: Represent the coordinates of the hyperbola's center.
These equations describe the geometric properties of the hyperbola and vary depending on the orientation of its axes.

Eccentricity of Hyperbola

The eccentricity of a hyperbola, denoted by e, measures how "stretched" the curve is. It is defined as the ratio of the distance of a point on the hyperbola from the focus to its perpendicular distance from the directrix. For a hyperbola, the eccentricity is always greater than 1 (e>1e). It can be calculated using the formula:

e= √1+b 2 a 2

Here:
  • a is the length of the semi-major axis.
  • b is the length of the semi-minor axis.

Perfect Square

Latus Rectum of Hyperbola

The latus rectum of a hyperbola is a line that passes through one of its foci and is perpendicular to the transverse axis. The endpoints of the latus rectum lie on the hyperbola, and its length is given by: Length of latus rectum= 2b 2 /a These properties are fundamental to understanding the geometry of a hyperbola.

1: Determine the eccentricity of the hyperbola x 2 /81−y 2 / 49=1.

Solution:

The equation of the hyperbola is x 2 /81−y 2 / 49=1. By comparing with the standard equation x 2 /a 2 − y 2 b 2 = 1, we get: a 2 = 81, b 2 =49a a = 9, b = 7 The formula for the eccentricity of a hyperbola is: Substituting the values of a and b :

e = 1 + 49/81

e = e = 130/81 Hence, the eccentricity of the given hyperbola is

2: If the equation of the hyperbola is (x−3) /36 − (y+5)/16 = 1, find the lengths of the major axis, minor axis, and latus rectum.

Solution:

The equation of the hyperbola is ( x−3) /36 − (y+5) / 16 =1 By comparing with the standard equation (x−h) / a −(y−k) / b =1, we get: h=3, k=−5, a =36, b =16h = 3

Length of the major axis :

2a=2×6=12 units

Length of the minor axis :

2b=2×4=8 units

Length of the latus rectum :

2b /a=2×16/6=32/6=5.33 units Hence, the lengths are:
  • Major axis: 12 units
  • Minor axis: 8 units
  • Latus rectum: 5.33 units

3: Find the eccentricity of the hyperbola whose latus rectum is 1/3 of its conjugate axis.

Solution:

Let the equation of the hyperbola be x / a −y b =1 The length of the conjugate axis is 2b , and the latus rectum is 2b /a. From the given condition: 2b /a=1/3×2b
b /a  = b/3 The eccentricity of a hyperbola is: e= √1+b a Substitute b=3a e= √1+(3a) / a
e= √1+9a) / a
e = √1 + 9 = √10
Hence, the eccentricity of the hyperbola is 10.

Hyperbola FAQs

Where are hyperbolas used in real life?

Hyperbolas are used in satellite navigation, physics (such as hyperbolic trajectories), and engineering (design of cooling towers).

What is a rectangular hyperbola?

A rectangular hyperbola is a special case where a=b. Its asymptotes are perpendicular, and the eccentricity is √2.

Who discovered the hyperbola?

The concept of the hyperbola was first studied by ancient Greek mathematicians like Apollonius, who classified conic sections.

How does the shape of a hyperbola change with eccentricity?

As eccentricity increases, the branches of the hyperbola become more open and stretched outward.

Why does a hyperbola have two branches?

The two branches represent the set of all points where the absolute difference in distances to the foci remains constant.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
008448982616
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.