Ratio and Proportion - Basics, Definition with Examples

Ratio and Proportion: In our daily lives, we usually compare things like sharing chocolates between friends or mixing water and juice in the right amount. This comparison and sharing in equal parts is what we learn in maths as ratio and proportion.

From dividing money to finding the right speed and distance, knowing what is ratio and proportion makes solving many maths problems much easier. So, to learn the basics of ratio and proportion, their definitions, simple formulas, and examples, keep reading.

What is Ratio and Proportion? 

In maths, when we compare two numbers or quantities by dividing them, it is called a ratio. For example, if there are 2 apples and 3 oranges, we can write the ratio as 2:3 or 2/3. It is read as “2 is to 3.” A ratio helps us see how much one thing is compared to another.

Now, when two ratios are equal, it is called a proportion. For example, if 2:3 is equal to 4:6, we can say that these two ratios are in proportion. We write this as 2:3 :: 4:6, which means “2 is to 3 as 4 is to 6.”

So, we can answer the question "what is ratio and proportion?" in simple words as: Ratio is used to compare two things. On the other hand, Proportion shows that two ratios are equal. 

Read More: Fun Math Activities for Kids to Develop Calculation Speed

Definition of Ratio

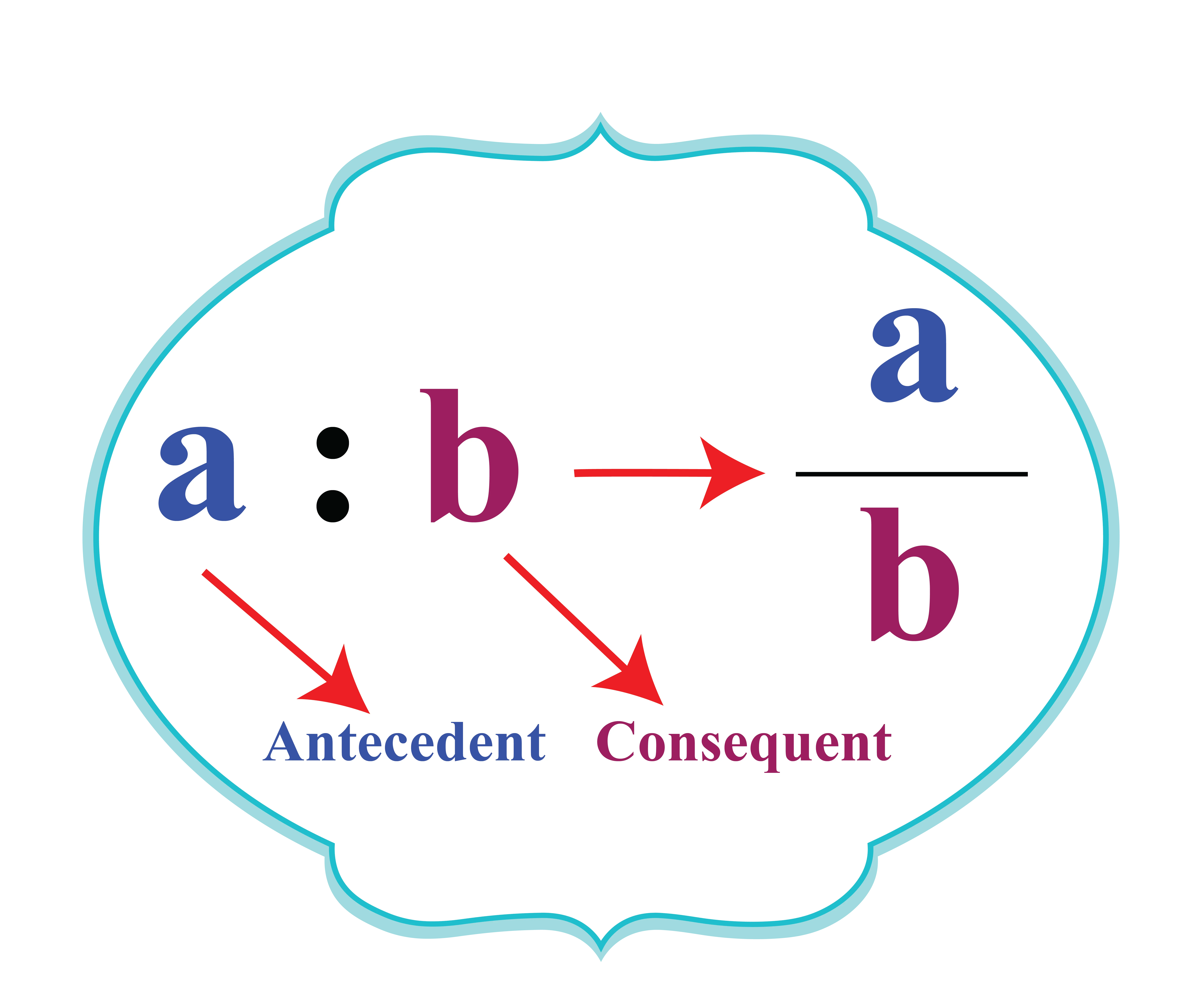
A ratio is a method that helps in comparing two quantities of the same kind. We find the ratio by dividing one quantity by the other. For example, if there are 4 red balls and 2 blue balls, the ratio of red to blue is 4:2, which means 4 is to 2. Ratios are written using a colon symbol (:) like a : b, where:

• a is called the antecedent.

• b is called the consequent.

Moreover, Ratio has no units and simply shows how much one value is compared to the other. Ratios can be made simpler by dividing both numbers by the same value. For example, 4:2 becomes 2:1 when divided by 2.

Read More: Quick Calculation Techniques for School Students

Definition of Proportion

Using Proportion we can show that two ratios are equal. If one ratio is the same as another, we say they are in proportion. We write this using a double colon (::). For example, if a : b = c : d, we can write it as a : b :: c : d, where:

• a and d are called the extreme terms.

• b and c are called the mean terms.

For example, the ratios 3:5 and 15:25 are equal because both become the same when written as fractions: 3 ÷ 5 = 0.6 and 15 ÷ 25 = 0.6. Since they are equal, we say they are in proportion. There are two types of proportion: Direct Proportion and Inverse Proportion.

• In direct proportion, when one value increases, the other also increases.

• In inverse proportion, when one value increases, the other decreases.

Read More: How to Prepare for Math Olympiads with Mental Maths

Key Properties of Proportion

To solve many proportion-related questions in maths, it is important for students to remember some key properties, as outlined below.

1. Addendo: If two ratios are equal, like a : b = c : d, then the sum of their first terms and second terms will also be in the same ratio. 

• So, a + c : b + d

2. Subtrahendo: If a : b = c : d, then the difference of the first terms and second terms will also be in the same ratio.

• So, a − c : b − d

3. Dividendo: If a : b = c : d, then the difference of the terms compared to the second term gives the same ratio.

• So, (a − b) : b = (c − d) : d

4. Componendo: If a : b = c : d, then the sum of the terms compared to the second term also gives the same ratio.

• So, (a + b) : b = (c + d) : d

5. Alternendo: If a : b = c : d, then we can switch the terms across the ratio.

• So, a : c = b : d

6. Invertendo: If a : b = c : d, then we can flip both sides and still keep the ratio equal.

• So, b : a = d : c

7. Componendo and Dividendo: If a : b = c : d, then the sum and difference of the terms can be written as a new ratio.

• So, (a + b) : (a − b) = (c + d) : (c − d)

Read More: Abacus vs. Vedic Maths: Which One is Better?

Difference Between Ratio and Proportion

Many students find it confusing to understand the difference between ratio and proportion, but it is actually simple. Let's know how.

• A ratio is used when we compare two similar quantities, like 3 pens to 5 pencils, which we write as 3:5.

• A ratio is shown using symbols like a colon (:) or a slash (/), for example, 4:5 or 4/5.

• On the other hand, proportion is used when two such ratios are equal. For example, if 3:5 and 6:10 are equal, we say they are in proportion.

• A proportion is shown using a double colon (::), like 4:5 :: 8:10.

So, the main difference between ratio and proportion is that a ratio is just a comparison, while a proportion shows that two ratios are equal.

Read More: Fun Math Activities for Kids to Develop Calculation Speed

Ratio and Proportion Formulas

To solve problems easily, students can remember these basic ratio and proportion formulas. They help in comparing values and checking if two ratios are equal.

Ratio Formula

The formula of a ratio is: a : b = a / b

This shows that a ratio compares two quantities by division. In this, a is the first number and b is the second number. Ratios do not have any units and help in showing how much one quantity is compared to the other.

If both terms in a ratio are multiplied or divided by the same non-zero number, the value of the ratio remains the same.

Proportion Formula

The formula of proportion shows that two ratios are equal: a : b = c : d

Or simply written as: a × d = b × c

This is known as cross-multiplication. If this multiplication on both sides gives the same value, then the two ratios are in proportion.

Ratio and Proportion Examples with Answers

Find out some easy ratio and proportion examples with answers that will make it easy for students to understand the concept of ratio and proportion here:

Example 1. Are the Ratios 6:9 and 10:15 in Proportion?

Solution:

Let's convert both ratios into fractions:

6:9 = 6 ÷ 9 = 0.666...

10:15 = 10 ÷ 15 = 0.666...

Since both the ratios are equal, they are said to be in proportion.

Answer: Yes, 6:9 and 10:15 are in proportion.

Enroll Now for Kids Online Classes

Example 2. Check Whether 14:21 and 20:35 are in Proportion

Solution:

Convert the ratios to fractions:

14:21 = 14 ÷ 21 = 2/3

20:35 = 20 ÷ 35 = 4/7

Since 2/3 ≠ 4/7, both ratios are not equal.

Answer: No, 14:21 and 20:35 are not in proportion.

Example 3. The income of Arjun is INR 15,000 per month and the income of Rakesh is INR 180,000 per year. Both spend INR 12,000 every month. Find the ratio of their savings.

Solution:

Arjun’s Savings:

Monthly = INR 15,000 - INR 12,000 = INR 3,000

Rakesh’s Monthly Income:

INR 180,000 ÷ 12 = INR 15,000

Rakesh’s Monthly Savings = INR 15,000 - INR 12,000 = INR 3,000

Now, Ratio of their savings = INR 3,000 : INR 3,000 = 1:1

Answer: The ratio of savings is 1:1, so they are also in proportion.

Example 4. Find the Ratio of the Length and Breadth of a Garden if the Length is 72 m and Breadth is 18 m.

Solution:

Length = 72 m
Breadth = 18 m

Ratio of length to breadth = 72 : 18

Divide both terms by 18:

72 ÷ 18 = 4
18 ÷ 18 = 1

So, 72:18 = 4:1

Answer: The ratio of length to breadth is 4:1

Example 5. Two Numbers Are in the Ratio 5:7. If Their Sum Is 96, Find the Numbers.

Solution:

Let the two numbers be 5x and 7x
Their sum = 5x + 7x = 12x = 96

x = 96 ÷ 12 = 8

So the numbers are:

5x = 5 × 8 = 40
7x = 7 × 8 = 56

Answer: The numbers are 40 and 56, and they are in the ratio 5:7.

These ratio and proportion examples will help students clearly understand how to solve different types of questions using basic mathematical operations.

Enhance Your Child’s Math Learning with CuriousJr

Is your child slow at doing math calculations and finding it hard to keep up in exams? Many students face this challenge, which can make learning stressful for both kids and parents.

That's why CuriousJr’s Mental Math Kids Online Classes offer a helpful way to support your child’s learning.

• These classes include interactive live sessions with two teachers so that your child gets more attention and clear explanations.

• The lessons use engaging animations and interactive elements to make learning interesting, while badges encourage learners to stay motivated.

• Your child will get tailored practice based on their needs and help with homework to reinforce what they learn.

• Daily performance tracking lets you see how your child is improving over time.

• And the cherry on top—these classes cost just INR 29, making it easy to give your child extra practice and confidence in math. Book a demo class today to make math enjoyable for your child.