Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
No, volume represents physical space and cannot be negative.
What is the significance of π\piπ in the formula?
π represents the ratio of a circle's circumference to its diameter. In the volume of a hemisphere formula, it ensures accurate calculation of the space enclosed by the curved surface and base.
Can the formula be used for irregular shapes?
No, the formula applies only to perfectly hemispherical shapes.
What is the relationship between the volume and surface area of a hemisphere?
Both depend on the radius, but surface area includes both the curved area and the circular base.
How does the volume change if the radius is halved?
When the radius of a hemisphere is halved, its volume decreases by a factor of 8. This is because the volume is proportional to the cube of the radius.
Example: If the radius of a hemisphere is originally 6 cm, its volume is 144πcm³
When the radius is halved (r = 3), the new volume is 18πcm³
Thus, the volume decreases from 144πcm³ to 18πcm³ showing a reduction by a factor of 8.
Volume of a Hemisphere: Definition, Formula, and Solved Examples
The volume of a hemisphere is the three-dimensional space it occupies. Learn the steps to calculate the volume of a hemisphere with simple formulas and solved examples for clarity.
Chandni 30 Jun, 2025
Share
Volume of a Hemisphere: Hemispheres are not just abstract geometric shapes; they’re all around us! From the curved dome of an igloo to the smooth shape of a bowl, hemispheres play a role in our everyday lives.
Have you ever wondered how much space these shapes occupy? Understanding the volume of a hemisphere isn’t just about math; it is useful in design, architecture, and calculating the capacity of objects like tanks or molds. In this blog, we will learn how to calculate the volume of a hemisphere with stepwise solved examples.
What is Hemisphere?
A hemisphere is a three-dimensional shape that results from cutting a sphere into two equal halves along its diameter. The term "hemi" means "half," and "sphere" refers to the round, ball-like 3D shape. Thus, a hemisphere is literally half of a sphere. It consists of a curved, half-spherical surface that forms the outer part of the shape and a flat circular base that forms the bottom of the shape when placed on a flat surface. Hemispheres are seen in nature and everyday life, such as :
Northern Hemisphere and Southern Hemisphere of Earth
Igloo structures in polar regions
The upper half of a tennis ball
Bowls in the kitchen
Domes in architecture
All of these shapes can help us understand what is the volume of a hemisphere in practical, real-life situations.
Volume of Hemisphere Definition
The volume of a hemisphere represents the amount of space it occupies or the capacity it can hold. For example, it helps determine how much liquid a hemispherical bowl can contain, the space inside a dome-shaped structure, or the material needed to create half of a sphere. The volume is measured in cubic units, such as cm 3 , m 3 or in 3 , to quantify this space accurately.
Volume of Hemisphere Formula
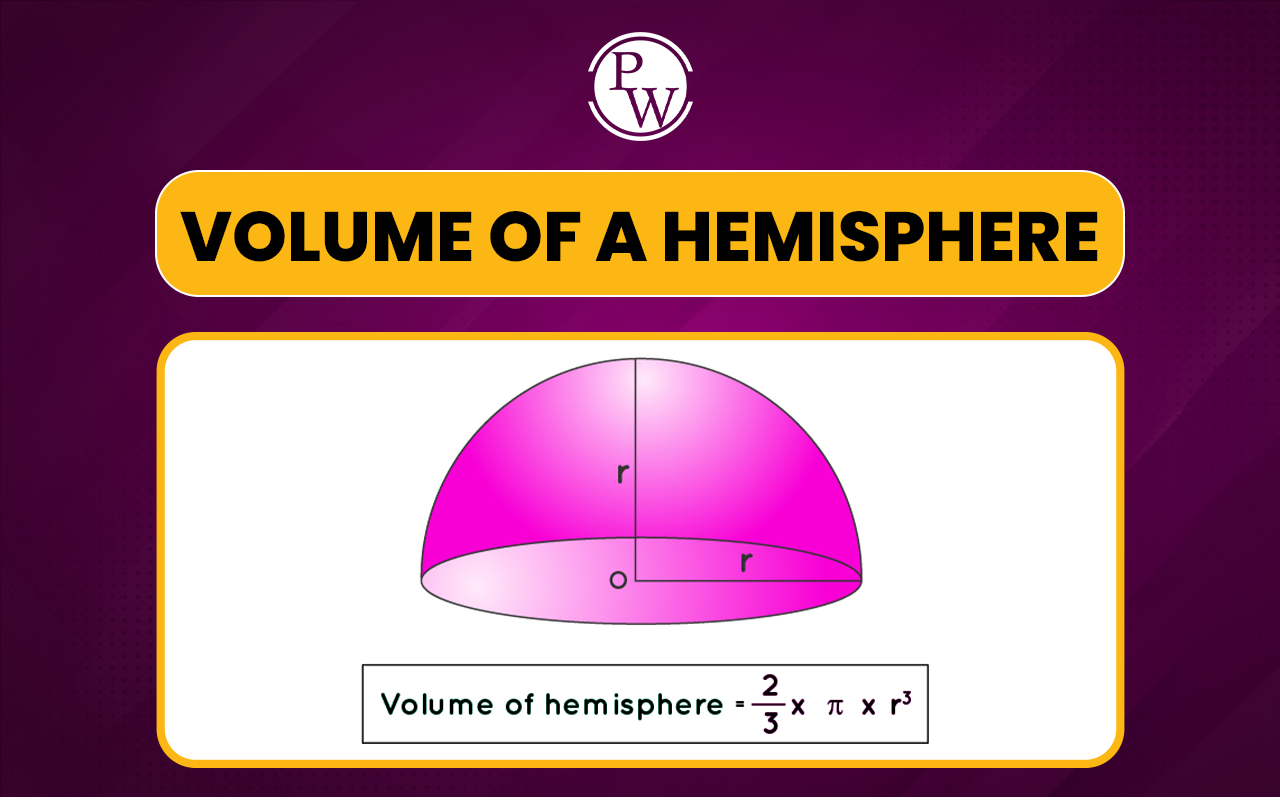
A hemisphere is essentially half of a sphere, which means its volume will also be half of the sphere's volume.
The formula to calculate volume of a sphere is 4/3πr 3
Since the hemisphere is half of the sphere, its volume can be calculated as 1/2× 4/3πr 3 Simplifying this, the formula for the volume of a hemisphere becomes 2 /3πr 3
A hemisphere is essentially half of a sphere, which means its volume will also be half of the sphere's volume.
The formula to calculate the volume of a sphere is: 4/3 × π × r³
Since a hemisphere is half of a sphere, its volume can be calculated as: 1/2 × 4/3 × π × r³ = 2/3 × π × r³
This is known as the hemisphere volume formula. It’s simple and easy to remember.
The volume of the hemisphere is two-thirds of the product of π and the cube of its radius. The volume of a sphere is experimentally proven to be two-thirds of the volume of a cylinder that has the same radius and a height equal to the diameter of the sphere.
To begin, consider the volume of such a cylinder. For a cylinder with radius r and height equal to 2r (the sphere's diameter), the volume is calculated as:
Volume of Cylinder = πr 2 × (2r) = 2πr 3
From this relationship, the volume of the sphere is two-thirds of the cylinder's volume: 2/3 × 2πr 3 = 4/3πr 3 Now, since a hemisphere is half of a sphere, its volume is simply half the volume of the sphere. Dividing the sphere's volume by 2 gives: 4/3πr 3 /2 = 2/3πr 3
Thus, the formula for the volume of a hemisphere is derived as 2/3πr 3
Here, r represents the radius of the hemisphere, and the formula calculates the three-dimensional space it occupies.
Using a Hemisphere Volume Calculator
Want to check your answer quickly? Use a hemisphere volume calculator online! All you need to enter is the radius, and the calculator will use the formula 2/3πr³ to give you the answer instantly. This helps when checking homework or solving tricky problems quickly.
So next time someone asks, “what is the volume of a hemisphere?”, just pull up a calculator and impress them with your skills.
Understanding the volume of hemisphere is not only important for math exams, but it also has real-life applications. From simple formulas like the hemisphere volume formula to fun activities and calculators, this topic can actually be quite exciting!
So next time you see a bowl, a dome, or even a globe—ask yourself: “What is the volume of a hemisphere like this?” You’ll know exactly how to find out!
Example 1: Find the volume of a hemisphere with a radius of 10 cm. Solution: Step 1: The radius (r) of the hemisphere is 10 cm. Step 2: Use the formula for the volume of a hemisphere: Volume of Hemisphere = 2/3πr³ Step 3 : Substitute r = 10 and π = 3.14 Volume of Hemisphere= 2/3 × 3.14 × (10) 3 Step 4 : Calculate: Volume of Hemisphere = 2/3 × 3.14 × 1000 The volume of the hemisphere is approximately 2093.33 cm³.Example 2: If the volume of a hemisphere is 45 cubic meters, it is melted and used to form smaller hemispheres with a volume of 9 cubic meters each. How many smaller hemispheres can be made? Solution: Let n be the number of smaller hemispheres formed. The relationship is: n × Volume of a smaller hemisphere = Volume of the larger hemisphere Substitute the values: n × 9 = 45 n = 45/9 n = 5 Five smaller hemispheres can be formed by melting the larger hemisphere. Example 3: Find the volume of a hemisphere with a diameter of 10 cm. Solution: Given: Diameter = 10 cm Thus, radius (r) = 10/2 = 5 cm. The formula for the volume of a hemisphere is 2/3πr 3 Substitute r = 5 and π=3.14 Volume= 2/3 × 3.14 × (5) ³ Volume= 2/3 × 3.14 × 125 Volume = 785/3 ≈ 261.67 cm ³ The volume of the hemisphere is approximately 261.67 cm ³ . Example 4: A hemisphere with a radius of 4 cm is fitted inside a cuboid, and then water is filled into the cuboid. Find the volume of water present in the cuboid. Solution: Step 1 : Dimensions of the cuboid:
Length (l) = 2r = 2 × 4 = 8 cm
Breadth (b) = 2r = 8 cm
Height (h) = r = 4 cm
Volume of the cuboid: = l × b × h = 8 × 8 × 4 = 256 cm ³ Volume of Hemisphere = 2/3πr³ Substitute r = 4 and π = 3.14 Volume of Hemisphere = 2/3 × 3.14 × (4) ³ Volume of Hemisphere = 2/3 × 3.14 × 64 = 401.92/3 ≈133.97cm³ Now, calculate the volume of water: Volume of Water = Volume of Cuboid−Volume of Hemisphere Volume of Water = 256 − 133.97 = 122.03 cm ³ The volume of water present in the cuboid is approximately 122.03 cm ³
Example 5: If the volume of a hemisphere is 5.236 m ³ , find the radius of the hemisphere.
Solution :
The formula for the volume of a hemisphere is 2/3πr³ We are given a volume of hemisphere, i.e., 5.236 m ³. Substituting this value into the formula: 5.236 = 2/3πr³ Multiply by 3/2 πr ³ = 7.854 Divide by π r ³ = 7.854/3.1416 ≈ 2.5 Take cube root: r = ∛ 2.5 ≈ 1.357 m
