Ascending Order Formula: Definition, Symbol, Examples

Ascending Order Formula: Ascending order pertains to the organization of numbers or items in a manner where they are progressively larger, moving from the smallest to the largest. This arrangement is notably observed on a number line, where numbers are read from left to right. Numbers can be organized in ascending order by either using commas to separate them or by employing the 'less-than symbol (<)' between numbers. For instance, 1, 2, 3, 4, 5 or 1 < 2 < 3 < 4 < 5.

Have you encountered situations where an abundance of important folders, files, or documents seemed potentially beneficial, yet due to their sheer volume, locating the right one became a challenge? Many of these challenges can be resolved by adopting a specific pattern or arrangement. Organizing items in ascending order offers an effective method of compiling and presenting data.

Ascending Order Meaning

Ascending signifies a state of progression or growth. Thus, when a set of values, a map, or a list displays a sequence from the smallest to the largest, it is termed an ascending set/map/list. This progression can manifest in various domains, spanning alphabets, weights, heights, and time. For instance, consider the phrase, 'The rocket is ascending into the sky.' In this context, it indicates that as the rocket embarks on its journey, its distance from the ground is consistently increasing as it ventures into outer space. This provides a broad understanding of the term 'ascending.'

Now, let's transition our focus to 'ascending order.'

What is Increasing Order?

Ascending order pertains to the organization of data in a sequence that progresses from the smallest to the largest value. It is alternatively referred to as increasing order. To illustrate, consider the following set of numbers: [6, 2, 8, 4, 0]. Let's endeavor to reorganize them in an increasing order:

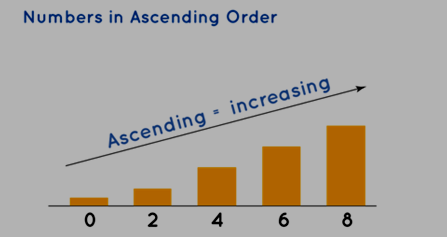
Ascending order of numbers

Consequently, the numbers mentioned above are restructured in ascending order as [0, 2, 4, 6, 8] or 0 < 2 < 4 < 6 < 8. When arranging a given series of numbers in ascending order, a few principles should be borne in mind, as outlined below:

The initial value is consistently the smallest.

The progression should consistently follow from the smallest to the largest value.

The concluding value invariably represents the largest.

As an example, for the ascending arrangement: [49, 54, 89, 623, 810],

The number 49 is the smallest, hence it occupies the first position.

The number 810 is the largest, making it the final entry on the list.

Ascending Order Symbol

To depict a provided series of numbers in ascending order, there are two primary methods: utilizing commas (',') or employing the 'less than' symbol ('<'). The prevalent approach involves employing the 'less than' symbol, indicating that the number positioned on the left holds a smaller value than the number placed on the right side of the symbol. For instance, the arrangement 2 < 3 < 4 signifies ascending order.

Fractions in Ascending Order

Arranging fractions in ascending order entails organizing the provided fractions in a manner that they increase progressively. When it comes to fractions, there exist two approaches for establishing an ascending order:

Method 1: Converting fractions to decimals

A conversion of fractions into decimals can be accomplished by dividing the numerator by the denominator. Subsequently, these decimal representations can be ordered in ascending fashion by evaluating both the whole number component and the decimal fraction component.

Example: Organize the subsequent fractions in ascending order: 1/2, 2/5, 5/6, 3/5.

Solution: By transforming these fractions into their corresponding decimal forms, we obtain:

1/2 = 0.5

2/5 = 0.4

5/6 = 0.83

3/5 = 0.6

Observing that all these decimals possess a whole number component of 0, we direct our attention to the digit in the tenth place to establish their ascending order.

0.4 < 0.5 < 0.6 < 0.83

Hence, the fractions can be orderly arranged in ascending sequence as follows: 2/5 < 1/2 < 3/5 < 5/6.

Method 2: Through the conversion of disparate fractions into equivalent fractions sharing the same denominator.

By employing the second approach, we harmonize the denominators of the provided fractions to acquire a common denominator. This entails finding the Least Common Multiple (LCM) of the denominators. Subsequently, we multiply both the numerator and denominator by the same number. By comparing the numerators in the fractions obtained through this process, we subsequently arrange them in an ascending manner. Employing the same instance for elucidation:

Example: Sequence the subsequent fractions in ascending order: 1/2, 2/5, 5/6, 3/5.

Solution: Our objective is to convert the disparate fractions into equivalent forms with identical denominators. The fractions given are 1/2, 2/5, 5/6, 3/5.

LCM of {2, 5, 6} equals 30.

1/2 × 15/15 = 15/30

2/5 × 6/6 = 12/30

5/6 × 5/5 = 25/30

3/5 × 6/6 = 18/30

Having successfully converted all fractions to equivalent forms, the comparison of the numerators, i.e., 12 < 15 < 18 < 25, becomes straightforward.

Hence, we deduce 12/30 < 15/30 < 18/30 < 25/30.

Thus, the fractions are arranged in ascending order as follows: 2/5 < 1/2 < 3/5 < 5/6.

Ascending Order of Decimals

Decimals represent numerical values composed of both a whole number part and a fractional or decimal part, linked through a decimal point. To organize decimals in ascending order, begin by examining the whole number portion. If it is larger than the corresponding part in another decimal, it signifies that the number is greater than the other. For instance, 23.6 < 32.947 < 45.09. When multiple numbers share an equivalent whole number portion, such as 2.45 and 2.09, the focus shifts to the tenths place digit in each number. In this scenario, comparing the tenths place digits 4 and 0, it becomes evident that 0 < 4, leading to the conclusion that 2.09 < 2.45. Should the tenths place digits also be identical, the attention shifts to the hundredths place digits, followed by subsequent decimal places. This systematic process is employed to arrange decimals in ascending order.

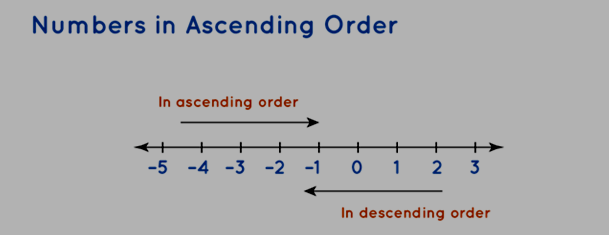
Ascending Order of Negative Numbers

Arranging negative numbers in ascending order involves organizing the provided negative numbers in a sequence that progresses from the smallest to the largest values. It's important to recognize that in the realm of negative numbers, the absolute values of smaller numbers surpass the absolute values of larger numbers. In the context of negative numbers, the highest numerical value adorned with a negative sign corresponds to the smallest value.

Example: Organize the following negative integers in ascending order: -34, -56, -4.

Solution: The provided negative integers can be orderly arranged in ascending sequence as shown below:

-56 < -34 < -4

Among the given three numbers, -4 holds the highest numerical value, while -56 represents the smallest value. To comprehend the concepts of ascending order and descending order of numbers on a number line, refer to the illustration provided below.

Ascending Order Examples

Example 1: Sequence the fractions in ascending order: 8/9, 4/9, 1/9, 6/9, 2/9.

Solution: The provided fractions share identical denominators, indicating that they are akin. Therefore, we solely need to examine the numerators and establish their order in an ascending manner.

The fractions can be systematically arranged in ascending order as depicted below:

1/9 < 2/9 < 4/9 < 6/9 < 8/9

Example 2: Organize the subsequent numbers in ascending order: 15, 7, 13, 6, 11, 17, 10.

Solution: The numbers can be systematically ordered in ascending sequence, resulting in 6 < 7 < 10 < 11 < 13 < 15 < 17.

Example 3: Arrange the following set in ascending order: {12.09, 11.6, 12.35, 6.72}.

Solution: When evaluating the provided decimals, it becomes apparent that 6.72 holds the smallest value since 6 is the minimum among the sets. In the case of 12.09 and 12.35, where the whole number portions are identical, we shift our focus to the digit residing in their tenth place. In 12.09, the tenth place digit is 0, while in 12.35, it is 3. Evidently, 0 < 3, affirming that 12.09 < 12.35. Thus, the given numbers can be methodically arranged in ascending order as follows: {6.72 < 11.6 < 12.09 < 12.35}.