
The half angle formulas are trigonometric identities that express the trigonometric functions of half an angle in terms of the trigonometric functions of the original angle. These formulas are particularly useful in trigonometry and calculus when dealing with angles that are smaller or more manageable than the original angle. There are different half-angle formulas for various trigonometric functions. Here are the half-angle formulas for sine, cosine, and tangent:
These half angle formulas are helpful for simplifying trigonometric expressions and for solving problems involving trigonometric identities. They are often used in calculus, geometry, and engineering to manipulate and solve equations involving trigonometric functions.
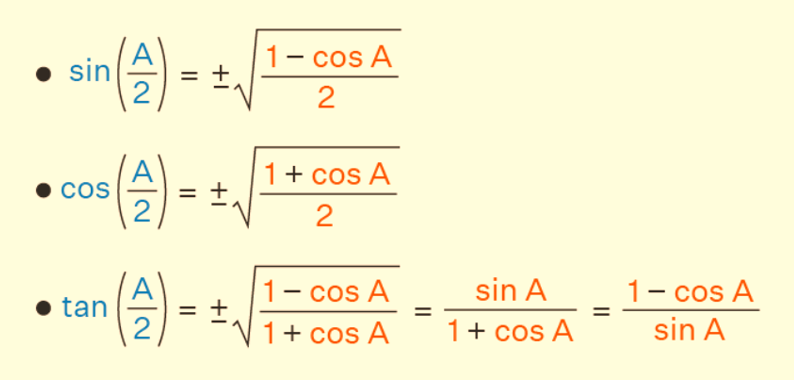
Half Angle Identities
Here are the popular half-angle identities for the trigonometric functions sine, cosine, and tangent:
- Half angle formula of sin: sin A/2 = ±√[(1 - cos A) / 2]
- Half angle formula of cos: cos A/2 = ±√[(1 + cos A) / 2]
- Half angle formula of tan: tan A/2 = ±√[1 - cos A] / [1 + cos A] (or) sin A / (1 + cos A) (or) (1 - cos A) / sin A
Half Angle Formulas Derivation Using Double Angle Formulas
To derive the half angle formulas, we start by using the double angle formulas, which express trigonometric functions in terms of double angles like 2θ, 2A, 2x, and so on. These double angle formulas are well-known:
For sine (sin): sin(2x) = 2sin(x)cos(x)
For cosine (cos): cos(2x) = cos^2(x) - sin^2(x) or cos(2x) = 1 - 2sin^2(x) or cos(2x) = 2cos^2(x) - 1
For tangent (tan): tan(2x) = 2tan(x) / (1 - tan^2(x))
Now, if we replace x with A/2 in each of these double angle formulas, we obtain the half-angle identities because 2x is equivalent to 2(A/2), which simplifies to A:
For sine (sin): sin(A) = 2sin(A/2)cos(A/2)
For cosine (cos): cos(A) = cos^2(A/2) - sin^2(A/2) or cos(A) = 1 - 2sin^2(A/2) or cos(A) = 2cos^2(A/2) - 1
For tangent (tan): tan(A) = 2tan(A/2) / (1 - tan^2(A/2))
These half angle identities are helpful in trigonometry for simplifying expressions and solving problems involving trigonometric functions when working with angles that are half of the original angles (A/2 in this case).

Half Angle Formulas of Sin Proof
To derive the half-angle formula for the sine function. Here's the step-by-step derivation: Starting with: cos(A) = 1 - 2sin^2(A/2) You can isolate sin^2(A/2) by rearranging the terms: 2sin^2(A/2) = 1 - cos(A) Then, divide both sides by 2 to find sin^2(A/2): sin^2(A/2) = (1 - cos(A)) / 2 Finally, to find sin(A/2), take the square root of both sides, noting that sin(A/2) could be either positive or negative depending on the quadrant in which A/2 lies: sin(A/2) = ±√[(1 - cos(A)) / 2] This result gives you the half-angle formula for the sine function. The ± sign accounts for the possibility of sine being positive or negative depending on the quadrant, as you correctly mentioned.Half Angle Formulas of Cos Derivation
the half-angle formula for the cosine function. Here's the step-by-step derivation: Starting with: cos(A) = 2cos^2(A/2) - 1 You can isolate cos^2(A/2) by rearranging the terms: 2cos^2(A/2) = 1 + cos(A) Then, divide both sides by 2 to find cos^2(A/2): cos^2(A/2) = (1 + cos(A)) / 2 Finally, to find cos(A/2), take the square root of both sides, noting that cos(A/2) could be either positive or negative depending on the quadrant in which A/2 lies: cos(A/2) = ±√[(1 + cos(A)) / 2] This result gives you the half angle formulas for the cosine function. The ± sign accounts for the possibility of cosine being positive or negative depending on the quadrant, as you correctly mentioned.Half Angle Formulas of Tan Derivation
We have tan (A/2) = [sin (A/2)] / [cos (A/2)] Using the half angle formulas of sin and cos, tan (A/2) = [±√(1 - cos A)/2] / [±√(1 + cos A)/2] = ±√[(1 - cos A) / (1 + cos A)] This is one of the formulas of tan (A/2). Let us derive the other two formulas by rationalizing the denominator tan (A/2) = ±√[(1 - cos A) / (1 + cos A)] × √[(1 - cos A) / (1 - cos A)] = √[(1 - cos A) 2 / (1 - cos 2 A)] = √[(1 - cos A) 2 / sin 2 A] = (1 - cos A) / sin A This is the second formula of tan (A/2). To derive another formula, let us multiply and divide the above formula by (1 + cos A). Then we get tan (A/2) = [(1 - cos A) / sin A] × [(1 + cos A) / (1 + cos A)] = (1 - cos 2 A) / [sin A (1 + cos A)] = sin 2 A / [sin A (1 + cos A)] = sin A / (1 + cos A) Thus, tan (A/2) = ±√[(1 - cos A) / (1 + cos A)] = (1 - cos A) / sin A = sin A / (1 + cos A).Half Angle Formulas Using Semi perimeter
The half-angle formulas for cosine, sine, and tangent functions using the semi-perimeter of a triangle. Here's a summary of the formulas you've derived: Cosine Half-Angle Formula: cos(A/2) = √[s(s - a) / bc] Sine Half-Angle Formula: sin(A/2) = √[(s - b)(s - c) / bc] Tangent Half-Angle Formula: tan(A/2) = sin(A/2) / cos(A/2) These formulas express the trigonometric functions of half an angle (A/2) in terms of the sides of a triangle (a, b, c) and the semi-perimeter (s). These identities are particularly useful in trigonometry and geometry when you're working with triangles and angles related to them.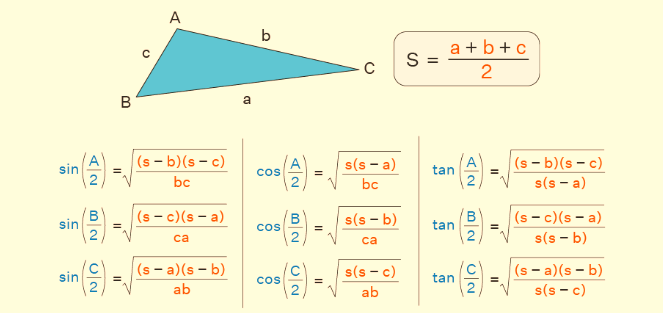
Half Angle Formulas Applications
Trigonometric Simplification: Half-angle formulas are used to simplify trigonometric expressions, making them more manageable and easier to work with. They can simplify complex expressions involving trigonometric functions, which is especially valuable in calculus and other advanced mathematics.
Geometric Problems: In geometry, half-angle formulas are applied to solve problems involving angles and shapes. They can be used to find missing angles, determine side lengths in triangles, and solve geometric constructions.
Navigation: Half-angle formulas are essential in navigation, such as in aviation and marine navigation. They help in calculating angles and distances, aiding pilots and navigators in determining their position and course.
Engineering: Engineers use half-angle formulas to analyze and design various structures and systems. For instance, in mechanical engineering, these formulas can be applied to determine angles in linkages, cam profiles, and gear mechanisms.
Physics: Half-angle formulas are employed in physics to solve problems related to wave propagation, interference, and diffraction. They are also useful in analyzing the behavior of light and electromagnetic waves.
Trigonometric Identities: Half-angle formulas are part of a larger set of trigonometric identities. These identities are widely used in mathematics, particularly in calculus, differential equations, and complex analysis.
Signal Processing: In signal processing and electrical engineering, half-angle formulas are used to analyze and process signals, such as determining phase shifts or analyzing oscillations.
Statistics: In statistical analysis, half-angle formulas can be applied to calculate measures of central tendency and dispersion, particularly in contexts where periodic or cyclical data is involved.
| Related Links | |
| Fibonacci Sequence Formula | Eulers Formula |
| Exponential Formula | Factorial Formula |
Half Angle Formulas
What are half-angle formulas?
What are the primary half-angle formulas?
When are half-angle formulas used?
Why are half-angle formulas useful?
How do I determine which sign (±) to use in half-angle formulas?










