Factorial Formula, Meaning , Formula and FAQs
The factorial formula of any non-negative whole number can be calculated using the formula n! = n × (n - 1)!. This formula is fundamental in mathematics and is used to calculate factorials
Anchal Singh12 Oct, 2023
Share
The factorial Formula of a whole number 'n' is calculated as the product of that number and all whole numbers from 'n' down to 1. For instance, the factorial of 4 is 4 × 3 × 2 × 1, which equals 24, and this is denoted as 4!. The study of factorial formula forms the foundation of various mathematical areas, including number theory, algebra, geometry, probability, statistics, graph theory, and discrete mathematics.
In 1677, Fabian Stedman, a British author, associated factorials with change ringing, a musical practice involving the ringing of multiple tuned bells. Then, in 1808, French mathematician Christian Kramp introduced the symbol for factorial, represented as 'n!'. If you're wondering how to calculate the factorial of a number, let's explore the process.What is Factorial Formula?
Factorial Formula is a mathematical operation that involves multiplying a whole number by all the natural numbers below it. It's typically denoted by the "!" symbol, which is located on the same computer keyboard key as the number "1." "n factorial," represented as "n!" is the result of multiplying the first n natural numbers together.
Factorial Formula Meaning
The notation "n!" or "n factorial" signifies the product of the first n positive integers, expressed as 1 · 2 · 3 · ... · n, which can also be represented as n(n-1)(n-2)…(3)(2)(1). For example, 5 factorial, denoted as 5!, is equal to 5 × 4 × 3 × 2 × 1, which equals 120. Example: To compute the factorial of a number using factorial formula , you can multiply that number by the factorial value of the preceding number. For instance, to find 6!, you multiply it by 120 (the factorial of 5), resulting in 720. Similarly, for 7!, you multiply 720 (the factorial value of 6) by 7, yielding 5040. In general, you can express n! as n × (n - 1)!.| n Factorial | n (n - 1) (n - 2) ....1 | n! = n × (n - 1)! | Result |
| 1 Factorial | 1 | 1 | 1 |
| 2 Factorial | 2 × 1 | = 2 × 1! | = 2 |
| 3 Factorial | 3 × 2 × 1 | = 3 × 2! | = 6 |
| 4 Factorial | 4 × 3 × 2 × 1 | = 4 × 3! | = 24 |
| 5 Factorial | 5 × 4 × 3 × 2 × 1 | = 5 × 4! | = 120 |
n Factorial Formula
There are two fundamental factorial formula for calculating n factorial: The first formula, n! = n(n-1)(n-2)…(3)(2)(1), directly follows from the definition of a factorial. It means that you multiply a given number by all the positive integers down to 1 to calculate its factorial. The second formula, n! = n × (n - 1)!, expresses that the factorial of any number can be obtained by multiplying that number by the factorial of the preceding number. For example, 8! = 8 × 7! and 9! = 9 × 8!, and so on. This concept extends to larger factorials, such as (n+1)! = (n+1) × n!. These formulas provide a straightforward way to compute factorials, and they can be applied to various examples.5 Factorial:
The value of 5 factorial, denoted as 5!, is equal to 5 × 4 × 3 × 2 × 1, which calculates to 120. You can also evaluate it using the factorial formula as 5! = 5 × 4! = 5 × 24 = 120.10 Factorial:
10 factorial, represented as 10!, is equivalent to 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1, resulting in a value of 3,628,800.0 Factorial:
Interestingly, zero factorial (0!) has a value of 1, not 0. This might seem counterintuitive, but it is indeed 1. To illustrate the pattern, consider: 1! = 1 2! = 2 × 1 = 2 3! = 3 × 2 × 1 = 3 × 2! = 6 4! = 4 × 3 × 2 × 1 = 4 × 3! = 24 This pattern is explained by the fundamental factorial formula: n! = n × (n - 1)! So, to find, for example, 3!, you can do 4! / 4, and similarly, 2! is 3! / 3, and so on. This formula captures the recursive nature of factorials. In this way, we could prove that 0 factorial is 1.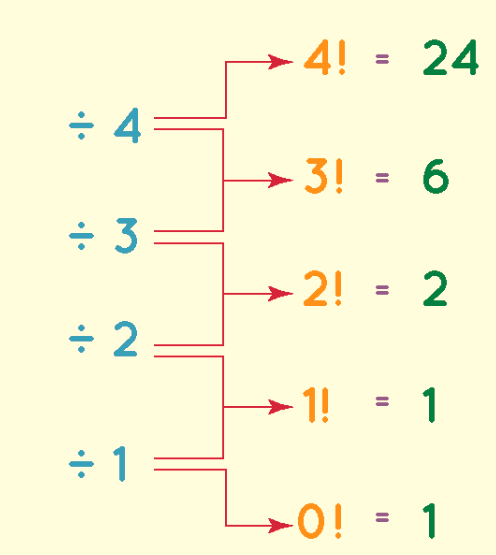
Alternative Way of Proving 0! = 1
In the realm of permutations and combinations, we learn that n! signifies the count of distinct ways to arrange 'n' different items. Viewing factorials from this perspective, 1! equals 1 because when there's just one item, there's only one way to arrange it. Similarly, 0! equals 1 because, even with zero items, we still have one way to arrange them, which is essentially no arrangement at all.Factorial of Hundred
100 factorials = 100 × 99 × 98 × .... × 3 × 2 × 1 = 9.332621544 E+157. This product is too big to calculate manually and hence a calculator is used. Here are some facts about hundred factorials:- 100 factorials has 24 trailing zeros in it.
- The total number of digits in 100! is 158.
- The exact value of 100 factorial is 93, 326, 215, 443, 944, 152, 681, 699, 238, 856, 266, 700, 490, 715, 968, 264, 381, 621, 468, 592, 963, 895, 217, 599, 993, 229, 915, 608, 941, 463, 976, 156, 518, 286, 253, 697, 920, 827, 223, 758, 251, 185, 210, 916, 864, 000, 000, 000, 000, 000, 000, 000, 000 (158 digits in total).
Factorial of Negative Numbers
Factorials for negative integers, like -1, -2, and so forth, are not defined. The factorial of a non-positive integer is undefined because it involves division by zero, which is a mathematically undefined operation. Consequently, negative integer factorials lack a conventional mathematical definition.Use of Factorial
Factorial formula find extensive use in permutation and combination problems. Permutation is the ordered arrangement of outcomes and can be computed with the formula: n Pr = n! / (n - r)! While combination represents a grouping of outcomes where order doesn't matter and is calculated with the formula: nCr = n! / [(n - r)! * r!]. In both these formulas, 'n' signifies the total number of available items, and 'r' represents the number of items to be selected. Let's illustrate this with the following examples: Example 1: In a group of 10 people, there are $200, $100, and $50 prizes to be distributed. This situation involves permutation because the order of prize distribution is significant. It can be calculated as 10P3 ways, where: 10P3 = (10!) / (10 - 3)! = (10!) / 7! = (10 * 9 * 8 * 7!) / 7! = 720 ways. Example 2: Three $50 prizes need to be distributed among a group of 10 people. In this case, it's a combination as the order of prize distribution doesn't matter (since all prizes are of the same value). It can be calculated using 10C3, where: 10C3 = (10!) / [3! * (10 - 3)!] = (10!) / (3! * 7!) = (10 * 9 * 8 * 7!) / [(3 * 2 * 1) * 7!] = 120 ways. These examples demonstrate how permutation and combination formulas help solve different scenarios involving the arrangement and selection of items. The factorial of a number 'n,' denoted as n!, is computed by multiplying all the integers from 1 to n. The formula for n factorial is n! = n × (n - 1)!. For instance, if we know that 8! is equal to 40,320, we can find the value of 9! as follows: 9! = 9 × 8! = 9 × 40,320 = 362,880. Factorials can be calculated for any whole number using the formula n! = n × (n - 1)!. Remarkably, the value of zero factorial is one, i.e., 0! = 1. However, negative integer factorials are undefined due to the mathematical impossibility of division by zero. Factorials for any whole number can be determined using the formula n! = n × (n - 1)!. Remarkably, the value of zero factorial is one, denoted as 0! = 1. However, negative integer factorials are not defined. Factorials are extensively used in the field of Permutation and Combination. Permutations (nPr) are computed with the formula n! / (n - r)!, while Combinations (nCr) are calculated using n! / [(n - r)! * r!].How to Calculate Factorial?
Factorials, denoted as n!, are calculated by multiplying all the integer numbers from 1 to n. The formula for the factorial of n is expressed as n! = n × (n - 1)!. For example, if we know that 8! equals 40,320, we can calculate 9! as follows: 9! = 9 × 8! = 9 × 40,320 = 362,880. Now, let's take a look at a factorial table that provides the values of factorial for the first 15 natural numbers:| n Factorial | Value |
| 1 Factorial | 1 |
| 2 Factorial | 2 |
| 3 Factorial | 6 |
| 4 Factorial | 24 |
| 5 Factorial | 120 |
| 6 Factorial | 720 |
| 7 Factorial | 5040 |
| 8 Factorial | 40,320 |
| 9 Factorial | 362,880 |
| 10 Factorial | 3,628,800 |
| 11 Factorial | 39,916,800 |
| 12 Factorial | 479,001,600 |
| 13 Factorial | 6,227,020,800 |
| 14 Factorial | 8,717,8291,200 |
| 15 Factorial | 1,307,674,368,000 |
Important Notes on Factorial
Essential facts about factorials, permutations, and combinations, which are fundamental concepts in combinatorics and mathematics. Here's a summary of the information you've mentioned:
Factorials: The factorial of any non-negative whole number n is calculated using the formula n! = n × (n - 1)!. The value of 0! (zero factorial) is defined to be 1: 0! = 1.
Factorials for negative integers are undefined.
Permutations (nPr): Permutations, denoted as nPr, are used to count the number of ways to arrange or select items from a set without replacement.
The formula for permutations is nPr = n! / (n - r)!, where n is the total number of items, and r is the number of items to be arranged or selected.
Combinations (nCr): Combinations, denoted as nCr, are used to count the number of ways to select items from a set without considering the order.
The formula for combinations is nCr = n! / [(n - r)! * r!], where n is the total number of items, and r is the number of items to be selected.
These concepts are essential in various areas of mathematics, probability, and statistics for solving problems involving counting and arrangement of elements in sets.
| Related Links | |
| Difference Quotient Formula | Eulers Formula |
| Exponential Formula | Consecutive Integers Formula |
Factorial Formula
What is the factorial formula?
The factorial formula, denoted as "n!," calculates the product of all positive integers from 1 to n. It is expressed as n! = n × (n - 1) × (n - 2) × ... × 3 × 2 × 1.
What is the value of 0 factorial (0!)?
The value of 0 factorial is defined as 1, represented as 0! = 1. This might seem counterintuitive, but it's a mathematical convention.
Are factorials defined for negative integers?
No, factorials for negative integers are not defined. Attempting to compute factorials for negative values leads to undefined results.
How can factorials be used in mathematical calculations?
Factorials are used in various mathematical contexts, such as permutations, combinations, and probability, to calculate the number of arrangements and selections of items.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.