
Euler's formula , named after the Swiss mathematician Leonhard Euler, encompasses two distinct mathematical concepts:
For Complex Analysis: Euler's formula, often referred to as Euler's identity, is a fundamental equation used to solve complex exponential functions. It establishes a profound relationship between trigonometric functions and complex exponentials.
For Polyhedra: Euler's formula, also known as Euler's characteristic, applies to non-self-intersecting Polyhedra. It describes a specific relationship between the number of faces, vertices, and edges in these three-dimensional geometric shapes.
In the following sections, we will delve into these two types of Euler's formulas and provide solved examples to illustrate their applications and significance.
What is Euler's Formula?
Euler’s Formula has been formulated into two terms one is with respect to Complex Analysis and the Other is Polyhedra
Euler's Formula for Complex Analysis:
Euler's formula for complex analysis relates a complex exponential to trigonometric functions and is written as:
e^ix = cos(x) + isin(x)
"e" is the base of the natural logarithm (approximately 2.71828).
"i" is the imaginary unit (where i^2 = -1).
"x" is a real number (angle in radians).
"cos(x)" represents the cosine of the angle.
"sin(x)" represents the sine of the angle.
This formula has profound applications in complex analysis and various scientific fields.
Euler's Formula for Polyhedra:
Euler's formula for Polyhedra, also known as Euler's characteristic, describes the relationship between the number of faces, vertices, and edges of a non-self-intersecting polyhedron:
faces + vertices - edges = 2
This formula is applicable to many different Polyhedra and is used in geometry to determine properties of three-dimensional shapes.
Euler's Formula For complex analysis
Euler's form of a complex number is a highly valuable representation that simplifies many calculations. It establishes a crucial link between trigonometric functions and complex exponentials. Euler's formula, defined for any real number x, is expressed as:
eix = cos x + isin x
Here, cos and sin are trigonometric functions, i is the imaginary unit, and e is the base of the natural logarithm. The interpretation of this formula can be taken in a complex plane, as a unit complex function eiθ tracing a unit circle, where θ is a real number and is measured in radians.
At first glance, this representation may appear perplexing—raising a real number to an imaginary exponent seems unconventional. However, there is a solid justification for this relationship, although we won't delve into a rigorous proof here. To gain some insight, consider the following approximate proof to understand why it holds true.
Proof
We use the following expansion series for e x :
e x = 1 + x + x 2 /2! + x 3 /3! + x 4 /4! + ... ∞
Now, we assume that this expansion holds true even if x is a Non real number. In a rigorous proof, even this assumption will have to be justified, but for now, let us take its truth to be granted, and use x = iθ.
e iθ = 1 + iθ + (iθ) 2 /2! + (iθ) 3 /3! + (iθ) 4 /4! + ... ∞
= 1 + iθ - θ 2 /2! - iθ 3 /3! + θ 4 /4! + ... ∞ (because i 2 = -1)
= (1 - θ 2 /2! + θ 4 /4! - ... ∞) + i (θ - θ 3 /3! + θ 5 /5! -... ∞)
The two series are Tylor Series Expansion for cosθ and sinθ thus
e ix = cos x + isin x
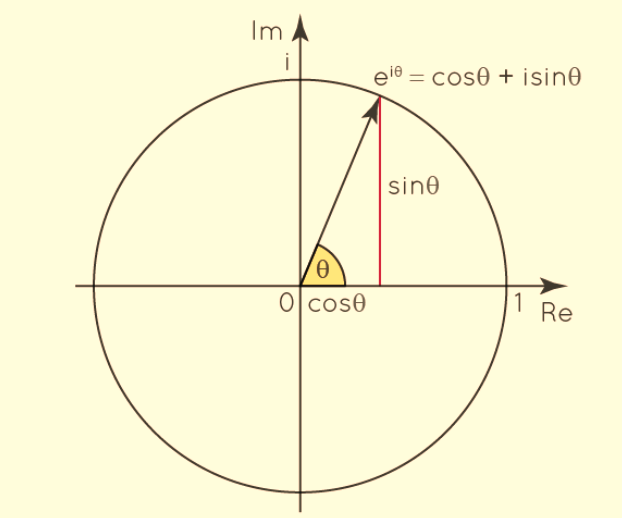
Euler's Identity
e iπ = cos π + isin π
e iπ = -1 + i (0) (as cos π = -1 and sin π = 0)
e iπ = -1 (or)
e iπ + 1 = 0
This is known as Euler's identity .
Euler's Formula For polyhedra
Polyhedra are three-dimensional solid shapes characterized by flat surfaces and straight edges. Examples of polyhedra include the cube, cuboid, prism, and pyramid. For any polyhedron that does not intersect itself, there exists a specific relationship among the number of faces (F), vertices (V), and edges (E). Euler's formula for polyhedra states that the sum of the number of faces and vertices is precisely two more than the number of edges. In a simpler format:
F represents the number of faces.
V represents the number of vertices.
E represents the number of edges.
Expressed as an equation, Euler's formula for a polyhedron can be written as:
Proof
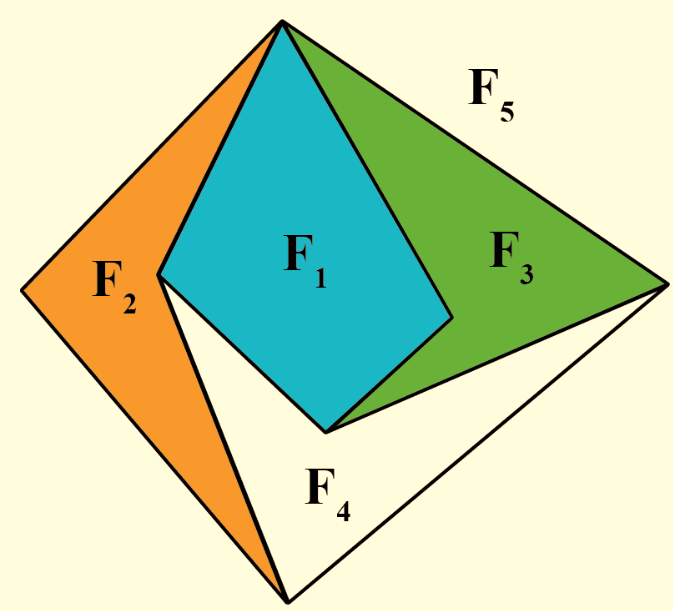
Euler's formula as it relates to graph theory and planar graphs. In the context of planar graphs and Euler's formula, the relationship is expressed as:
Number of Vertices (dots) - Number of Edges (lines) + Number of Regions (faces) = 2
This formula applies to planar graphs, where no edges (lines) cross each other when drawn on a plane. The number of regions corresponds to the areas created by the edges on the plane, which are also known as faces. Euler's formula for planar graphs provides a fundamental relationship between these three components and holds true for many types of planar graphs, including those representing three-dimensional shapes like cubes.
It's a powerful tool in graph theory and is used to analyze various properties of planar graphs and their connections between vertices, edges, and regions.
Solution for the Utilities Problem
Euler's formula is indeed a powerful tool in graph theory and planar graph analysis. Here's a summary of your argument:
Start with a graph representing the utility connections problem, where you have 6 vertices (houses and utilities) and 9 edges (connections).
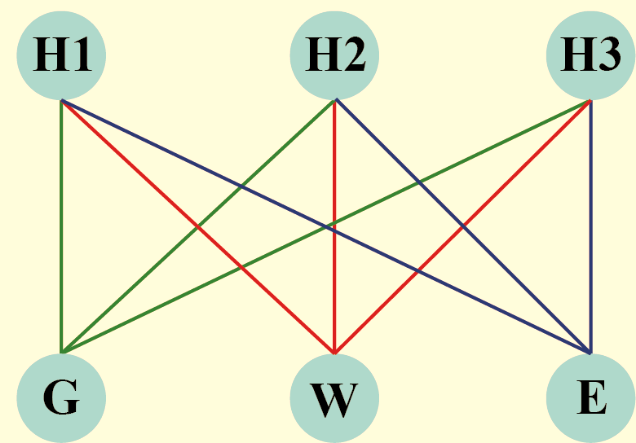
Apply Euler's formula for planar graphs:
F + V - E = 2
Calculate the number of faces (F) by rearranging the formula:
F = E - V + 2
Since F = 5, you consider a scenario where each of the 5 faces has 4 edges bounding them, which would require 10 edges.
However, the graph only has 9 edges, leading to a contradiction.
Based on Euler's formula, you conclude that it is impossible to represent this utility connection problem without intersecting edges.
You mention that when the two-dimensional planar graph is inflated into a solid, it becomes an octahedron, which has 8 faces, 6 vertices, and 12 edges, confirming the validity of Euler's formula.
This proof effectively demonstrates how Euler's formula can be used to analyze the impossibility of certain planar graphs, such as the utility connections problem, without intersecting edges. Well done!
What is Euler's Formula Used For?
Euler's formula is a versatile tool and can be expressed in its more general form as:
F+V−E=X
Here,
X represents the Euler characteristic, which can take on various values depending on the topology of the space being studied. While it's commonly 2 for surfaces like spheres and 1 for surfaces like tori, it can indeed have different values for more complex spaces and shapes.
Euler's formula is not limited to polyhedra but can be used to analyze any three-dimensional space or topological surface. It provides valuable insights into the relationships between the number of faces, vertices, and edges in a given structure.
In the context of regular polyhedra, Euler's graph theory indeed proves that there are exactly five regular polyhedra, known as the Platonic solids.
To verify the existence of a simple polyhedron with 10 faces and 17 vertices, Euler's formula can be applied as follows:
F (number of faces) is 10.
V (number of vertices) is 17.
E (number of edges) can be calculated using Euler's formula rearranged as
= E=V+F−2.
=17+10−2=25
E=17+10−2=25
When these values are plugged into Euler's formula:
10+17−25=2
The result is 2, which satisfies Euler's formula. However, it's important to note that this calculation alone doesn't guarantee the existence of such a polyhedron. Further analysis and geometric considerations are needed to determine the actual feasibility and characteristics of such a structure.
Verification of Euler's Formula for Solids
Euler's formula to verify the characteristics of a square pyramid and a triangular prism. Euler's formula indeed holds true for these simple polyhedra:
Square Pyramid:
Number of faces (F) = 5
Number of vertices (V) = 5
Number of edges (E) = 8
Using Euler's formula:
F+V−E=5+5−8=2
The result is 2, which satisfies Euler's formula.
Triangular Prism:
Number of faces (F) = 5
Number of vertices (V) = 6
Number of edges (E) = 9
Again using Euler's formula:
F+V−E=5+6−9=2
Once more, the result is 2, confirming that Euler's formula holds for the triangular prism as well.
These examples illustrate the versatility of Euler's formula in describing and verifying the characteristics of various Polyhedra and solid shapes. It's a fundamental principle in geometry and graph theory.
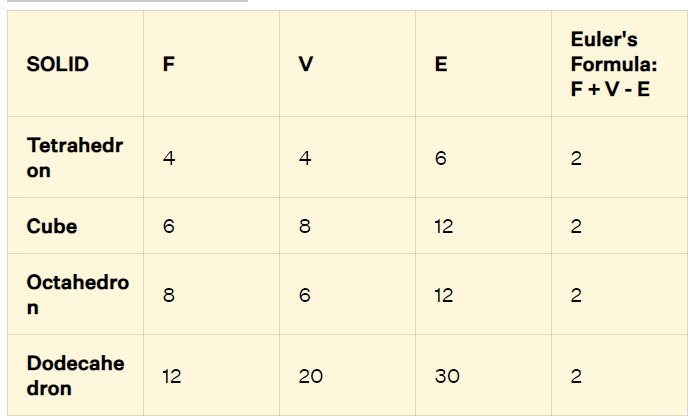
Euler's Formula Explanation
Indeed, there are five Platonic solids for which Euler's formula can be demonstrated. These solids are the cube, tetrahedron, octahedron, dodecahedron, and icosahedron. Let's apply Euler's formula to these complex Polyhedra to illustrate how it holds true for each of them.
| Related Links | |
| Complex Number Division Formula | Probability |
| Probability formula | Consecutive Integers Formula |
Euler's Formula FAQs
What is Euler's Formula?
Who was Leonhard Euler, and why is he associated with this formula?
What is the significance of Euler's Formula?
How is Euler's Formula used in graph theory?










