
The Fibonacci Sequence Formula is a numerical series that commences with 0 and 1, with each subsequent number being the sum of the two preceding ones. Consequently, the sequence appears as follows: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so forth. This sequence is attributed to Leonardo Pica, also known as Fibonacci, an Italian mathematician who introduced it to the Western world in his book Liber Abaci in 1202. The Fibonacci sequence is often associated with "nature's hidden code" and is observable in the spiral patterns of various natural phenomena such as sunflowers, daisies, broccoli, cauliflowers, and seashells. Let's delve further into its intriguing properties and significance.
The Fibonacci Sequence Formula is an infinite sequence that starts with 0 and 1, and every subsequent number is the sum of the two preceding ones. The first two terms are 0 and 1. Here are the first 20 terms of the Fibonacci sequence:
What is the Fibonacci Sequence Formula?
The Fibonacci Sequence Formula is an infinite sequence that starts with 0 and 1, and every subsequent number is the sum of the two preceding ones. The first two terms are 0 and 1. Here are the first 20 terms of the Fibonacci sequence:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181.
| Terms of Fibonacci Sequence | |
| F0 = 0 | F10 = 55 |
| F1 = 1 | F11 = 89 |
| F2 = 1 | F12 = 144 |
| F3 = 2 | F13 = 233 |
| F4 = 3 | F14 = 377 |
| F5 = 5 | F15 = 610 |
| F6 = 8 | F16 = 987 |
| F7 = 13 | F17 = 1597 |
| F8 = 21 | F18 = 2584 |
| F9 = 34 | F19 = 4181 |
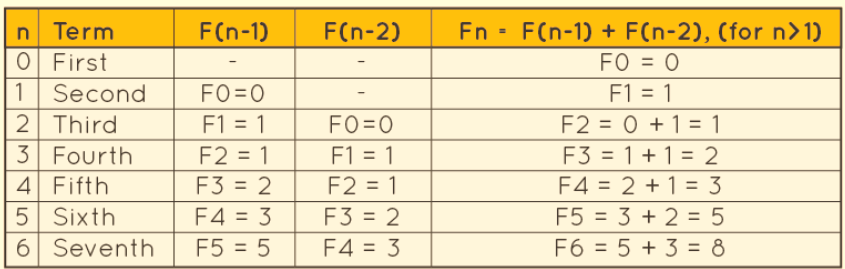
Indeed, the Fibonacci Sequence Formula is characterized by the relationship you mentioned: Fn = Fn-1 + Fn-2 for n > 1. This recursive nature is a fundamental feature of the sequence.
The significance of the Fibonacci Sequence Formula is indeed remarkable. Its presence in nature, such as in the arrangement of leaves, tree branches, and spiral patterns, highlights its connection to natural phenomena. Moreover, its applications extend to various fields, including mathematics, science, art, and finance. In mathematics, it's a fascinating subject for study and offers insights into many mathematical concepts. In science, it can describe growth patterns in populations and even patterns in the cosmos.
Artists often incorporate Fibonacci-related patterns into their work to create aesthetically pleasing compositions. Additionally, the sequence's role in finance and stock market analysis, where it can help predict trends, adds to its practical importance. The Fibonacci Sequence is, therefore, a versatile and intriguing mathematical concept with wide-ranging applications.
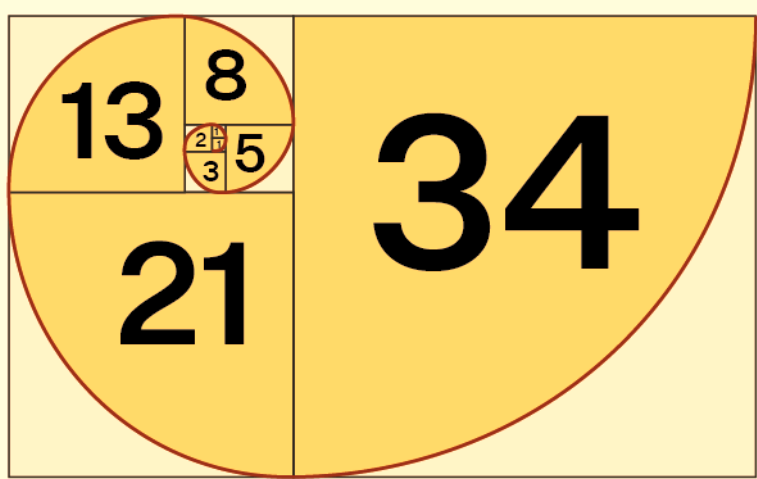
the Fibonacci spiral and how it relates to the golden ratio, a captivating mathematical concept. The way the Fibonacci sequence and the golden ratio intertwine to create this spiral pattern is truly fascinating. It's a testament to the ubiquity of these mathematical ideas in both nature and human design.
The golden ratio's presence in various aspects of art, architecture, and even nature has intrigued mathematicians, artists, and scientists for centuries. Its aesthetic appeal and balance are often leveraged in creative endeavors. The Fibonacci spiral and the golden ratio are indeed subjects of ongoing exploration and application in diverse fields, showcasing the enduring relevance of mathematical concepts in our world.
Fibonacci Formula Spiral
The Fibonacci sequence formula for "Fn" is established through a recursive process, with the initial values set as F0 = 0 and F1 = 1. This formula, denoted as Fn = Fn-1 + Fn-2 for n > 1, allows us to calculate each term in the sequence. In this context, "Fn" represents the (n+1)th number in the sequence, while "Fn-1" and "Fn-2" are the two preceding numbers. Using this formula, we can compute subsequent terms of the Fibonacci sequence. For instance, given that the first two terms are 0 and 1, we find the 3rd term as follows: F3 = F1 + F2 = 0 + 1 = 1. This method can be extended to determine all the terms in the sequence. It's worth noting that in this approach, F0 is considered the first term (not F1), and "Fn" represents the (n + 1)th term in the sequence.
Fibonacci Sequence Formula Properties
- Fibonacci numbers are closely tied to the golden ratio, and you can approximately calculate any Fibonacci number using the golden ratio. This is often referred to as the "Binet formula," which states that Fn ≈ (Φ^n - (1-Φ)^n)/√5, where Φ is the golden ratio, approximately equal to 1.618034. For example, F7 can be found as [(1.618034)^7 - (1-1.618034)^7] / √5 = 13.
- As the Fibonacci sequence progresses, the ratio of successive terms converges toward the golden ratio. This convergence can be observed when looking at the sequence of ratios, such as A/B, where A and B are consecutive Fibonacci numbers.
| A | B | A/B |
| 2 | 3 | 1.5 |
| 3 | 5 | 1.6 |
| 5 | 8 | 1.6 |
| 8 | 13 | 1.625 |
| 144 | 233 | 1.618055555555556 |
| 233 | 377 | 1.618025751072961 |
3. Another interesting pattern is that every third number in the sequence, starting from 2, is a multiple of 2. Similarly, every fourth number, starting from 3, is a multiple of 3, and every fifth number, starting from 5, is a multiple of 5, and so on. 4. The Fibonacci sequence extends below zero by using F-n = (-1)^(n+1) * Fn. For example, F-4 = (-1)^5 * F4 = (-1)^3 = -3. The sum of the first n terms of the Fibonacci sequence can be calculated using Σi=0n Fi = Fn+2 - 1, where Fn is the nth Fibonacci number. (Note: the sequence starts with F0.) For instance, the sum of the first 10 terms of the sequence is found as 12th term - 1 = 89 - 1 = 88, which can be expressed mathematically as Σi=0^9 Fi = F11 - 1 = 89 - 1 = 88. The Fibonacci Sequence has connections to other mathematical concepts, including the Lucas numbers and Pascal's Triangle.
Applications of Fibonacci Sequence Formula
The Fibonacci Sequence Formula is pervasive across diverse fields, including nature, music, and the human body. It plays a crucial role in:
- Music, where it influences the organization of notes and the harmonic proportions.
- Coding, as it's used in computer algorithms, parallel and distributed systems for efficient problem-solving.
- Various scientific domains like high-energy physics, quantum mechanics, and cryptography, where it aids in solving complex problems.
- Biology, helping model growth patterns in plants and the arrangement of leaves on stems.
- Financial analysis, where it's applied to identify trends in stock prices and other financial data.
In essence, the Fibonacci Sequence Formula applications are far-reaching and extend into numerous aspects of our world.
| Related Links | |
| Difference Quotient Formula | Probability |
| Effect Size Formula | Consecutive Integers Formula |
Fibonacci Sequence Formula
What is the Fibonacci series?
Who discovered the Fibonacci series?
What is the Fibonacci formula?
What is the significance of the Fibonacci series?










