
An Exponential Function Formula is a fundamental mathematical function with diverse applications in the real world. It is employed to model exponential growth or decay, calculate investments, simulate population dynamics, and more. This article will delve into the rules, properties, graphs, derivatives, and exponential series, and provide examples of exponential function formula.
What is Exponential Function?
An exponential function formula can be represented as f(x) = ax, where "x" is a variable, and "a" is a constant referred to as the base of the function, with the condition that "a" must be greater than 0. The base often utilized for exponential functions is the transcendental number "e," which is approximately equal to 2.71828.
Exponential Function Formula
An exponential function formula is expressed through the formula f(x) = ax, wherein the variable x serves as the exponent. The shape of the exponential function formula curve is determined by the exponential function and is highly influenced by the value of x. This mathematical function is significant and follows the general form:
f(x) = ax
In the context of this exponential function formula:
The base "a" must be a positive constant, and it should not equal 1.
The variable "x" can take on any real number.
The function is undefined for values of "x" within the range of -1 < x < 1.
In this equation:
f(x) = ax
Here, "x" is the variable, and "a" represents the constant base of the function.
The behavior of the exponential curve, whether it experiences growth or decay, depends on the characteristics of the exponential function. Any quantity that increases or decreases by a consistent percentage at regular intervals can be described by either exponential growth or exponential decay.
Exponential Growth
Exponential growth is characterized by a slow initial increase in quantity, followed by a rapid and accelerating growth rate over time. The growth becomes faster and more pronounced as time progresses, which is often described as an "exponential increase."
The formula that defines exponential growth is typically expressed as:
y=a(1+r) x
Where:
"y" represents the final quantity or value after growth.
"a" is the initial quantity or value.
"r" is the growth rate expressed as a percentage.
"x" is the time or number of periods.
This formula illustrates how the initial quantity "a" increases exponentially over time due to the growth rate "r." As time "x" increases, the quantity "y" grows at an accelerating rate.
Exponential Decay
Exponential decay is characterized by a rapid initial decrease in quantity, followed by a slower and gradually decreasing rate of change over time. The rate of decrease becomes slower and less pronounced as time progresses, which is often referred to as an "exponential decrease."
The formula that defines exponential decay is typically expressed as:
y=a(1−r) x
Where:
"y" represents the final quantity or value after decay.
"a" is the initial quantity or value.
"r" is the decay rate expressed as a percentage.
"x" is the time or number of periods.
This formula illustrates how the initial quantity "a" decreases exponentially over time due to the decay rate "r." As time "x" increases, the quantity "y" decreases at a decelerating rate.
Exponential Function Graph
The figure illustrates the graphs of exponential function formula, where the exponent "n" increases. As "n" becomes larger, the curves indeed become steeper and the rate of growth accelerates. This phenomenon is a fundamental characteristic of exponential functions. For values of "x" greater than 1, it's evident that the values of "y," denoted as f_n(x), increase as "n" increases. In other words, as the exponent "n" grows, the exponential growth of the function becomes more pronounced for values of "x" greater than 1. This graph exemplifies the concept of exponential growth in mathematical functions.
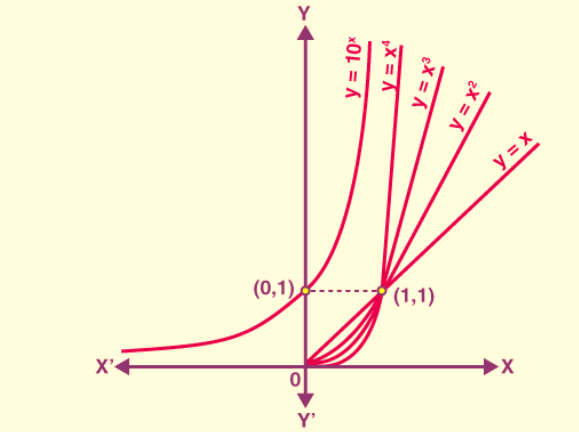
The nature of polynomial functions is indeed dependent on their degree. As the degree of a polynomial function increases, so does its growth rate. However, there is a class of functions that grow faster than polynomial functions, and that is the exponential function represented by y = f(x) = ax, where "a" is greater than 1. In comparison to any positive integer "n," this exponential function, f(x), is considered to grow faster.
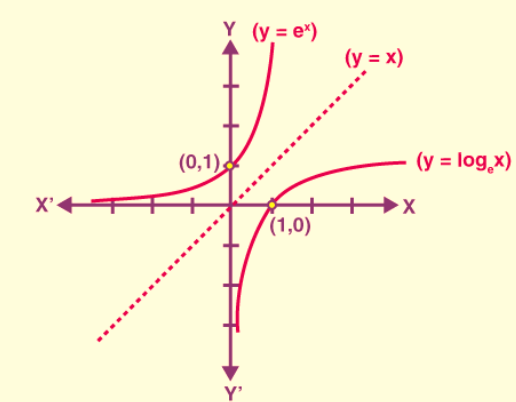
An exponential function with a base greater than 1, i.e., a > 1, can be defined as y = f(x) = ax. The domain of the exponential function encompasses the entire set of real numbers (R), and its range consists of all positive real numbers. Notably, the exponential function is always increasing, and it consistently includes the point (0, 1) on its graph. Additionally, the function approaches values very close to zero when "x" is predominantly negative.
A common type of exponential function is the one with base 10. This is often referred to as a common exponential function. However, when we choose the transcendental number "e" as the base, we obtain the natural exponential function, represented by y = ex. This function holds great significance in mathematics.
For values of "a" greater than 1, the logarithm of "b" to the base "a" is denoted as x if ax = b. This relationship is expressed as loga(b) = x when ax = b, and it defines the logarithmic function.
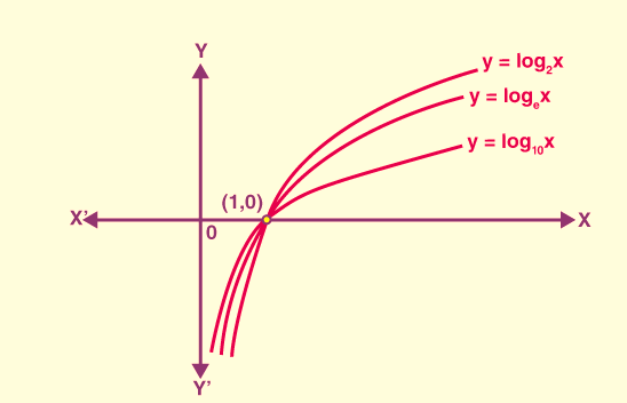
- When the base "a" is equal to 10, the resulting function is known as a common logarithm, and when the base "a" is "e," it is referred to as a natural logarithm, often denoted as "ln(x)." Here are some important observations regarding logarithmic functions with a base "a" greater than 1:
- The domain of a logarithmic function consists only of positive real numbers because the meaning of logarithmic functions is undefined for negative values.
- Despite its domain being limited to positive real numbers, the range of the logarithmic function encompasses all real values, denoted as "R."
- When we graph logarithmic functions and move from left to right along the x-axis, these functions exhibit an increasing behavior. In other words, as the input values increase, the corresponding output values also increase.
- The graph of a logarithmic function never intersects or crosses either the x-axis or the y-axis, although it appears to approach them. This behavior is a distinctive feature of logarithmic functions.
- Logap = α, logbp = β and logba = µ, then aα = p, bβ = p and bµ = a
- Logbpq = Logbp + Logbq
- Logbpy = ylogbp
- Logb (p/q) = logbp – logbq
Exponential Function Formula Derivative
Now, let's delve into the derivative of exponential functions. The derivative of e^x with respect to x is e^x, which can be expressed as d(e^x)/dx = e^x.
A special property of the exponential function f(x) = e^x is that its derivative is equal to the function itself, represented as follows:
f'(x) = e^x = f(x)
This property is significant because it distinguishes exponential functions from many other types of functions. The derivative of e^x is itself, highlighting the unique and consistent growth of exponential functions.
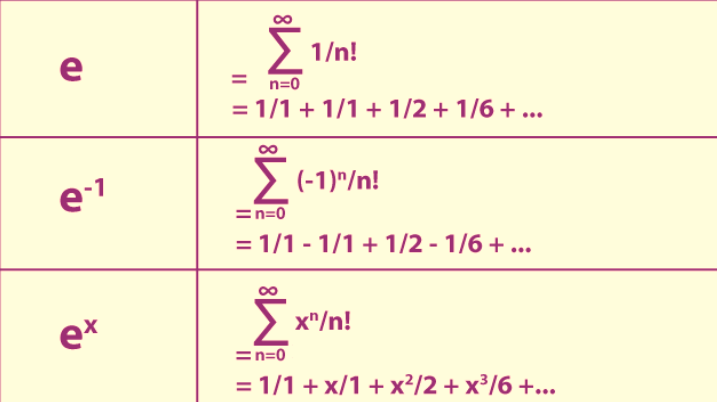
Exponential Series
The exponential series are given below.
Exponential Function Properties
The graph of the exponential function y = 2^x.
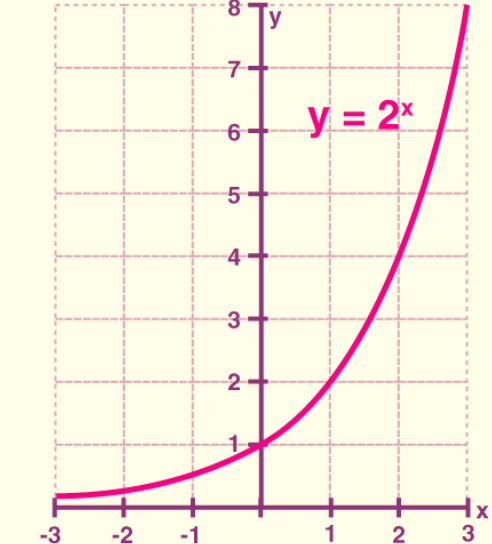
Exponential Function Graph for y = 2x
- The properties of the graph of an exponential function when the base is greater than 1, such as y = a^x, where "a" is greater than 1. Here's a recap of these properties:
- The graph passes through the point (0, 1). This is a fundamental characteristic of exponential functions.
- The domain of the function includes all real numbers, meaning it's defined for any real value of "x."
- The range of the function consists of all positive real numbers (y > 0).
- The graph is always increasing as "x" increases. This is due to the exponential growth behavior.
- The graph is asymptotic to the x-axis as "x" approaches negative infinity, meaning it gets closer and closer to the x-axis but never touches it.
- The graph increases without bound as "x" approaches positive infinity, indicating that the function grows infinitely larger as "x" becomes more positive.
- The graph of an exponential function is continuous, which means there are no breaks or discontinuities in its graph.
- The graph is also smooth, implying that it has no sharp corners or abrupt changes in direction. It exhibits a continuous, flowing behavior.
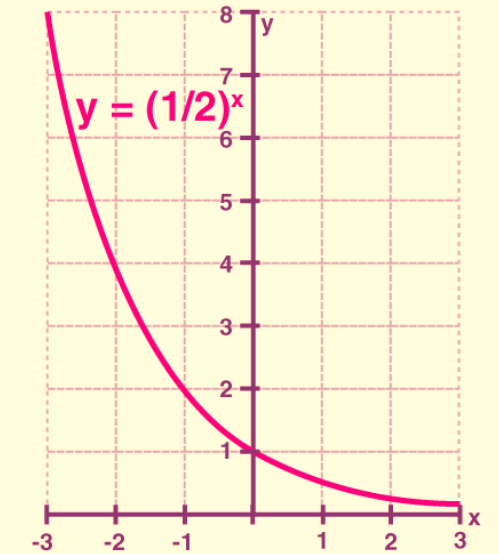
Exponential Function Graph y=2-x
The properties you've listed align with those of a linear function with a negative slope:
The line passes through the point (0, 1).
The domain includes all real numbers, meaning it's defined for any real value of "x."
The range consists of y > 0, as the line is decreasing.
It forms a decreasing graph, which is characteristic of linear functions with a negative slope.
The line is asymptotic to the x-axis as "x" approaches positive infinity.
The line increases without bound as "x" approaches negative infinity.
The graph is continuous with no breaks or discontinuities.
It forms a smooth graph, meaning it exhibits a continuous, unbroken, and linear behavior.
These properties are associated with linear functions, not exponential functions. Exponential functions typically exhibit exponential growth (if the base is greater than 1) or exponential decay (if the base is between 0 and 1), and their properties differ accordingly.
Exponential Function Rules
Some important exponential rules are given below:
If a>0, and b>0, the following hold true for all the real numbers x and y:
- ax ay = ax+y
- ax/ay = ax-y
- (ax)y = axy
- axbx=(ab)x
- (a/b)x= ax/bx
- a0=1
- a-x= 1/ ax
Exponential Functions Examples
The examples of exponential functions are:
- f(x) = 2x
- f(x) = 1/ 2x = 2-x
- f(x) = 2x+3
- f(x) = 0.5x
Exponential Function Formula Examples
Question 1:
Simplify the exponential function 2x – 2x+1 using exponential function formula
Solution:
Given exponential function: 2x – 2x+1
Using the property ax * ay = ax+y, you can rewrite 2x+1 as 2x * 2.
Now, factor out the term 2x:
2x – 2x+1 = 2x – 2x * 2 = 2x(1 - 2) = 2x(-1) = -2x
Therefore, the simplification of the given exponential function 2x – 2x+1 is -2x.
Question 2:
Solve the exponential equation: (¼)x = 64 using exponential function formula
Solution:
Given exponential equation: (¼)x = 64
Using the exponential rule (a/b)x = ax/bx, we get:
(1/4)x = 43
Since 1x equals 1, we have:
(1)(4-x) = 43
Now, equate the powers:
4-x = 3
Solving for x:
x = 4 - 3
x = 1
So, the solution to the exponential equation (¼)x = 64 is x = 1.
| Related Links | |
| Difference Quotient Formula | Probability |
| Effect Size Formula | Consecutive Integers Formula |
Exponential Function Formula
What is an exponential function?
What does the "x" represent in the exponential function?
What are some real-world applications of exponential functions?
How is exponential growth different from exponential decay?










