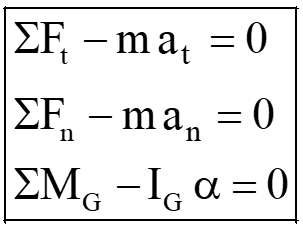D'Alembert's Principle: In engineering, some problems involve understanding what makes objects move and how they move. This falls under the branch of dynamics known as "kinetics." Kinetics is a branch of mechanics that deals with the study of forces and their effects on the motion of particles and rigid bodies. In engineering mechanics, understanding the kinetics of particles and rigid bodies is fundamental to solving practical engineering problems. D'Alembert's Method is a versatile technique that aids in the analysis of particles and rigid bodies. By introducing inertial forces and torques, this method simplifies the solution of complex dynamics problems.
D'Alembert's Principle
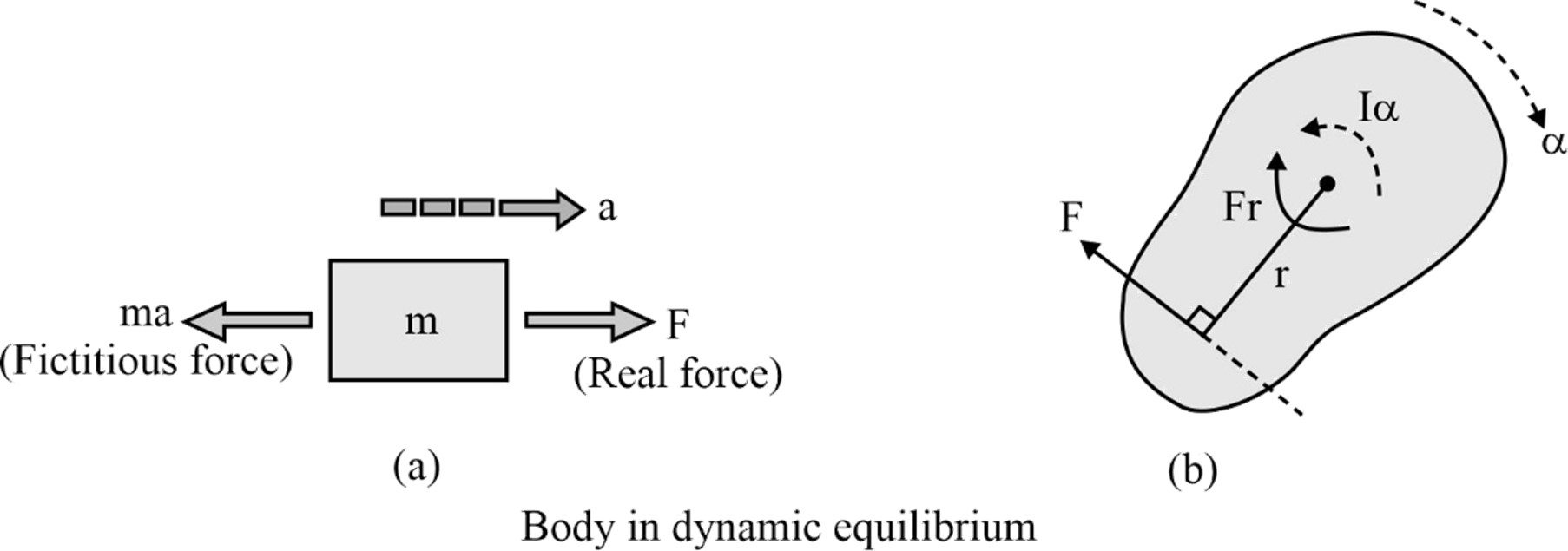
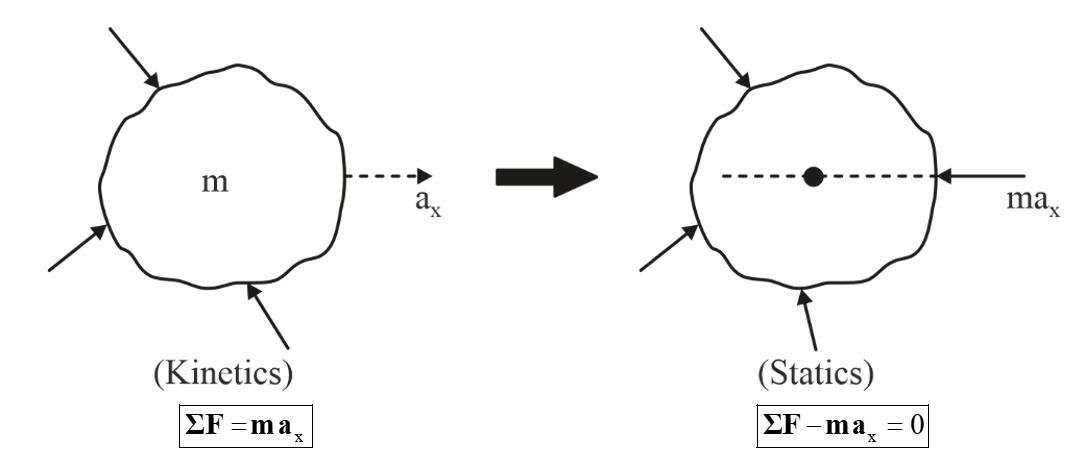
D'Alembert's Principle is a powerful tool used in engineering mechanics to analyze the motion of particles and rigid bodies subjected to forces and moments. Named after the French mathematician and physicist Jean le Rond d'Alembert, this principle is another form of Newton’s second law of motion. The application of D'Alembert's principle brings the transformation of a dynamic problem into an equivalent static problem. This principle is particularly useful when analyzing accelerating systems or systems in non-inertial reference frames.
As per this principle, “a body is in a state of dynamic equilibrium under the combined influence of external forces and inertia forces.” Dynamic equilibrium is an equilibrium state where the particle remains balanced under influence of external forces and inertia force, even though there exists a non-zero external resultant force externally acting upon it.
D'Alembert's Principle for a Particle
For a particle, this principle signifies that a body achieves a state of dynamic equilibrium through the combined influence of both the actual force and the introduced fictitious force (i.e., inertia force) ma. (Inertia force acts in the direction opposite to the acceleration)
 Note:
In a curvilinear motion, the dynamic behaviour of the particle can be analysed by using the following equations;
Note:
In a curvilinear motion, the dynamic behaviour of the particle can be analysed by using the following equations;
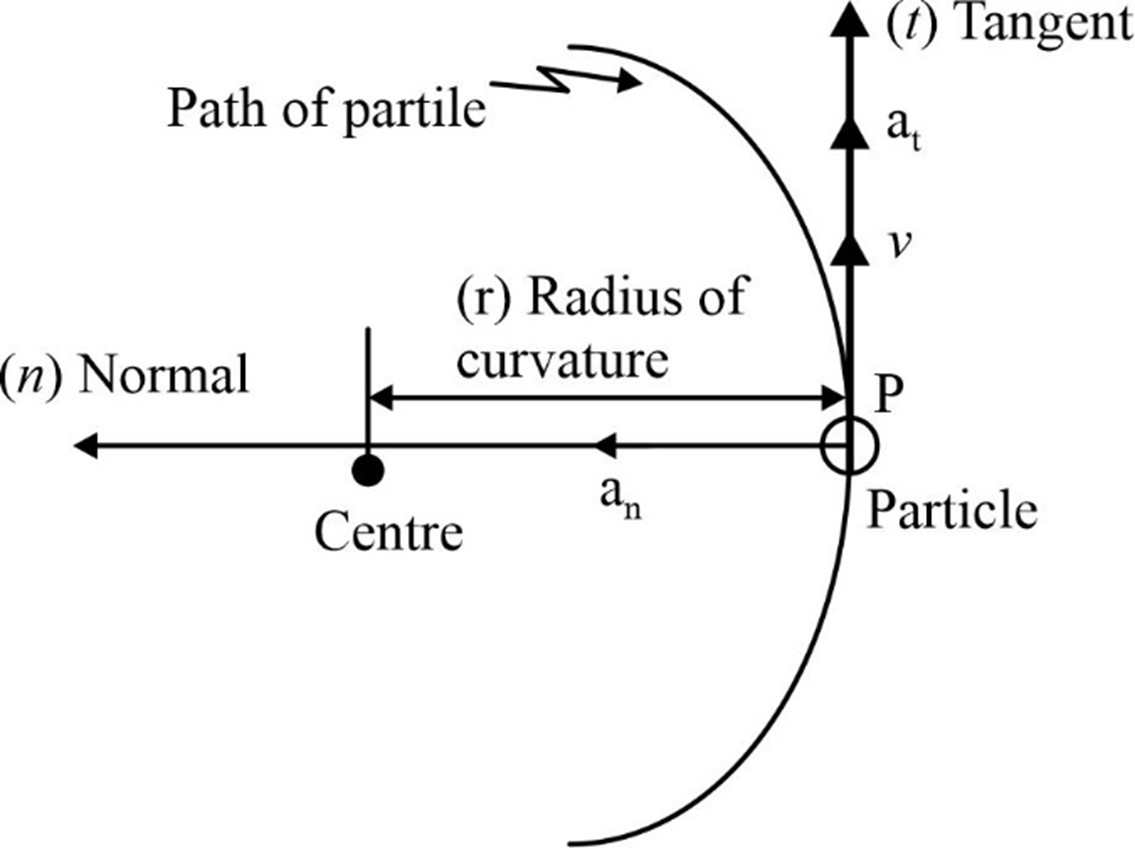 As per D'Alembert's principle, we can write the equation for above condition;
As per D'Alembert's principle, we can write the equation for above condition;
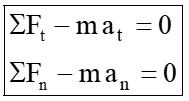
D'Alembert's Principle for a Rigid Body
For a rigid body, this principle signifies that a rigid body undergoing rotational or general motion achieves a state of dynamic equilibrium by introducing an inertia force and an inertia torque. In the case of a rotating body, the net moment (M G ) around its centre of mass can be counteracted by the inertial torque (I G a), where I G is the moment of inertia about COM and a is angular acceleration.
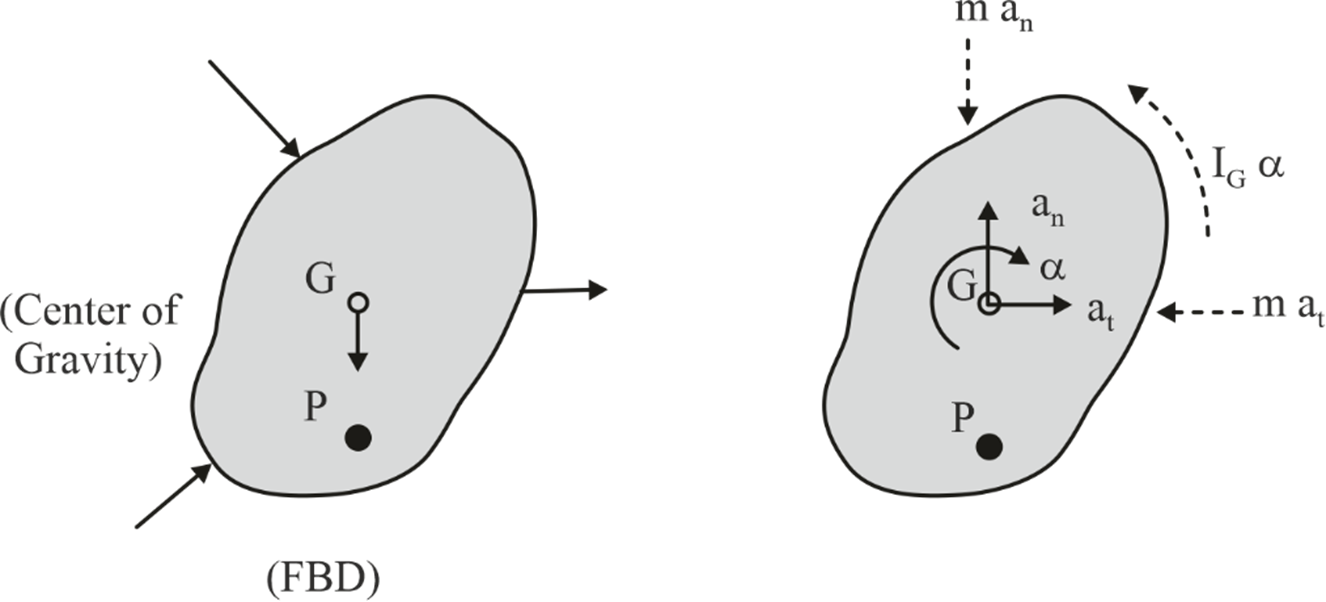 When a rigid body engages in motion, whether it's translation, rotation, or a combination of both, its dynamic behaviour is controlled by equations.
When a rigid body engages in motion, whether it's translation, rotation, or a combination of both, its dynamic behaviour is controlled by equations.