
Friction
Friction is an essential concept in the field of engineering mechanics that plays a crucial role in understanding the behavior and interaction of objects in motion. Friction force, also known as frictional force, arises whenever there is a tendency for one surface to slide along another. In such cases, the contact surfaces experience forces that act in a direction opposing the sliding motion. These opposing forces are referred to as friction forces.
In the equilibrium problems we have studied so far, we often assumed frictionless surfaces at the points of contact. However, it is important to note that this assumption of frictionless surfaces is an idealization. In reality, all surfaces possess some degree of roughness.
Cause of Dry Friction (Sliding Friction/ Coulomb’s Friction)
- Friction arises from the resistance encountered when minute projections on the surfaces come into contact. These microscopic projections interlock, leading to frictional forces.
-
Additionally, the material of the two bodies in contact contributes to the resistance to motion due to adhesive properties, which are a result of the intra-molecular forces of attraction.
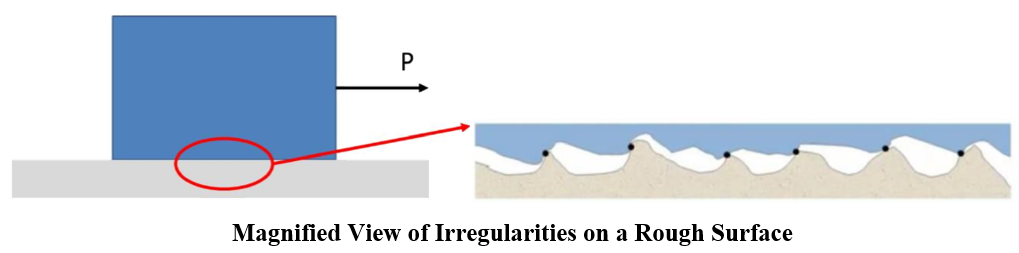
Mechanism of Dry Friction
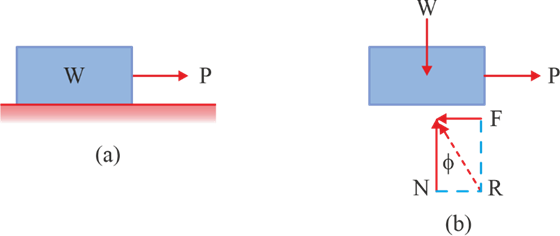
In the experiment, a solid block of weight ‘W’ rests on a rough horizontal surface, and it is subjected to a horizontal force, denoted as 'P,' that gradually grows from zero to a level capable of initiating motion in the block and giving it a noticeable velocity. As a horizontal force 'P' is gradually increased, the block experiences a tangential friction force 'F' opposing the motion, as shown in the block's free-body diagram. In the FBD shown, the total force 'R' on the block due to the supporting surface is the resultant force of 'N' and 'F'.
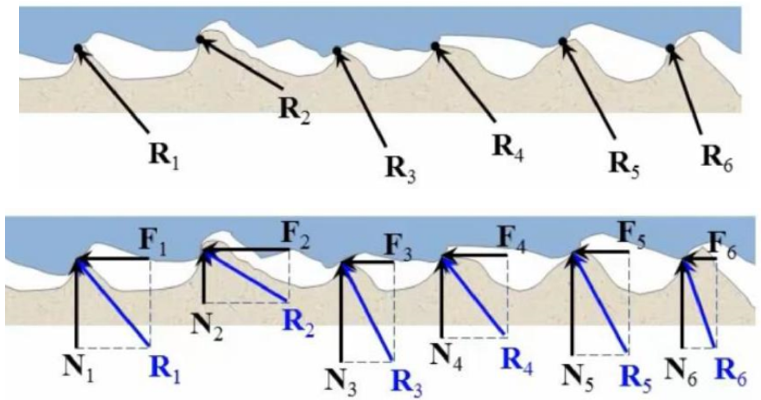
Examining the magnified view of the irregularities on the mating surfaces helps visualize the mechanical action of friction. The support between the surfaces is intermittent, occurring at the mating humps. The direction of reactions on the block (e.g., R 1 , R 2 , R 3 ) depends on the geometric profile and local deformation at each contact point. The total normal force 'N' is the sum of the components of 'R' in the normal direction, while the total frictional force 'F' is the sum of the tangential components of 'R'.
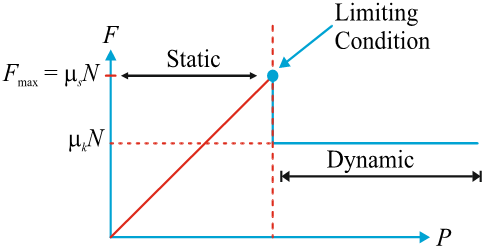
When the surfaces are in motion, the contacts mainly occur on the tops of the humps, resulting in smaller tangential components of 'R' compared to when the surfaces are at rest. This observation explains why the force 'P' required to maintain motion is typically lower than the force necessary to initiate motion when the irregularities are more engaged. By conducting the experiment and recording the friction force F as a function of P, a relationship is obtained (as shown in figure). At P= 0, no friction force exists due to equilibrium. As P increases, F matches and opposes P until the block starts slipping. During this period, the block remains in equilibrium, satisfying the equilibrium equations. Once the block slips, the friction force slightly and abruptly decreases.
Static Friction
The portion of the graph in the above figure that extends until the point of slippage or impending motion is referred to as the static friction range. Static friction refers to the force that resists the motion of an object when it is at rest and an external force is applied to move it. The magnitude of static friction can vary, depending on the force applied, but it always acts in the opposite direction to the impending motion. The friction force can take any value within this range, ranging from zero up to the maximum value.
By experimental investigation it is concluded that the maximum static friction or limiting friction, denoted as (F S ) max , is directly proportional to the normal force N. This relationship can be expressed as:
(F S ) max = μ s × N
Here, μ s represents the coefficient of static friction, which serves as the proportionality constant.
Note:
- If P < μ s N ⇒ Body remains static.
- If P = μ s N ⇒ Body is on the verge of motion. (static)
- If P > μ s N ⇒ Body starts moving.
Kinetic Friction
Kinetic friction comes into play when an object is in motion relative to another surface. The force of kinetic friction, denoted as F k , is generally slightly smaller than the maximum static friction force. Similar to static friction, the kinetic friction force is also directly proportional to the normal force. Therefore, we can express the relationship as:F k = μ k × N
Here, μ k represents the coefficient of kinetic friction.Laws of Dry Friction
In 1781, Coulomb presented a concise summary of his research on friction, outlining the laws that govern its behavior. The laws of friction can be summarized as follows:- The maximum static friction is proportional to the normal force.
- Friction is independent of contact area but depends on surface roughness.
- The coefficient of static friction is always greater than the coefficient of kinetic friction.
Friction Angle
It is the angle between normal force and resultant of normal and friction force when the body is on the verge of moving.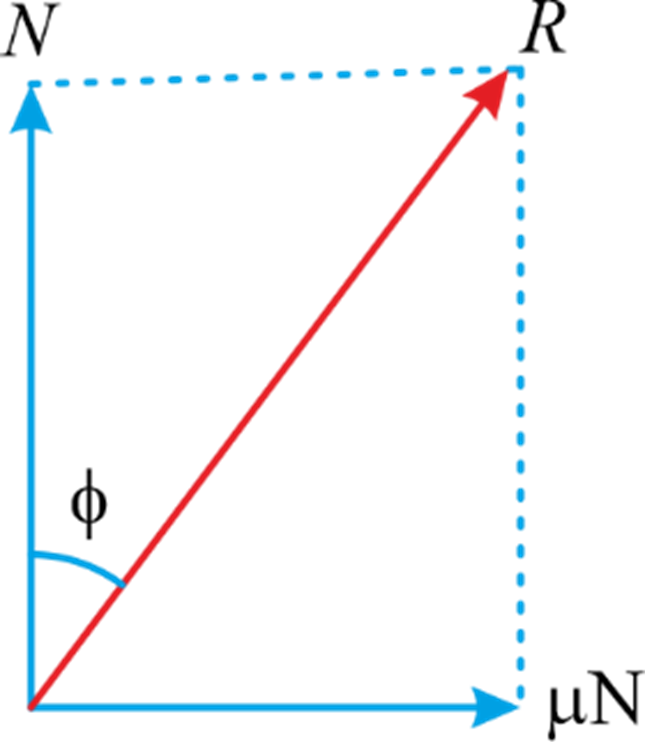 From the above graph, by using trigonometry we can write,
From the above graph, by using trigonometry we can write,
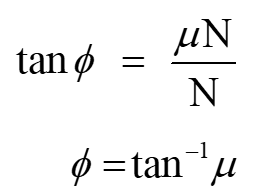
Angle of Repose
If a body is resting on an inclined surface, then the angle of repose is the maximum angle at which the body can be at rest without slipping down.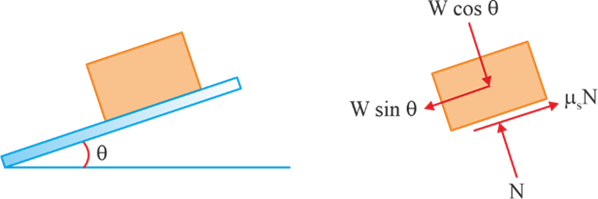
Consider the instant at which the block is just about to start the motion for giving inclination to the surface.
∑F x = 0μ s N – W sin θ = 0
W sin θ = μ s N . . . (i)
∑F y = 0
N – W cos θ = 0
W cos θ = N . . . (ii)
Dividing Equation (i) by Equation (ii), we get
tan θ = μ s (⸪ tan Φ = μ s )
tan θ = tan Φ
Angle of repose (θ) = Angle of friction (Φ)
Shifting of Normal Reaction and Tipping
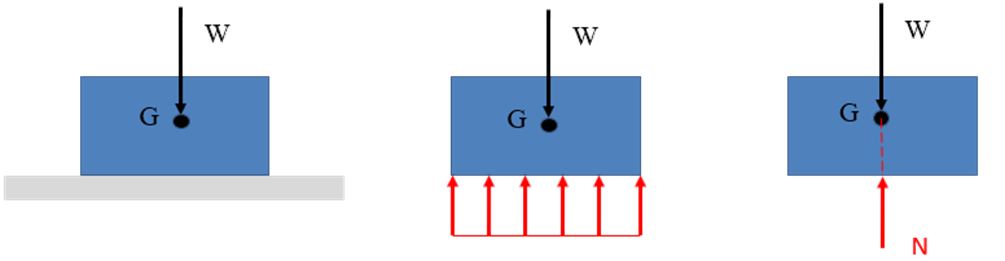
When two surfaces come into contact, one surface applies a normal reaction on the other. The normal reaction is distributed over the entire surface of contact does not act only at one point. For example, when a uniform block rests on a horizontal surface, the normal reaction is distributed uniformly over the block's surface as shown in the figure. To achieve translatory and rotatory equilibrium, the normal reaction should balance the weight of the object and pass through its centre.
 Now, let's consider a box and a force P is applied to the box as shown, the normal reaction will shift to balance the torque produced by the applied force and friction, around the center of mass. The distance x represents the displacement of the normal reaction when the box is sliding on the surface.
Now, let's consider a box and a force P is applied to the box as shown, the normal reaction will shift to balance the torque produced by the applied force and friction, around the center of mass. The distance x represents the displacement of the normal reaction when the box is sliding on the surface.
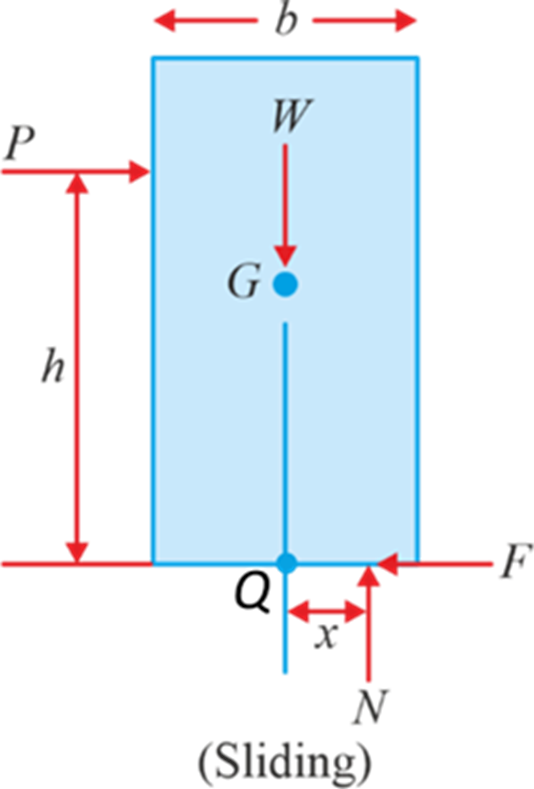
∑M Q = 0
P × h – N × x = 0
P × h = N × x
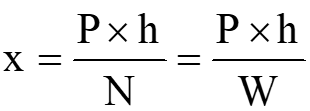
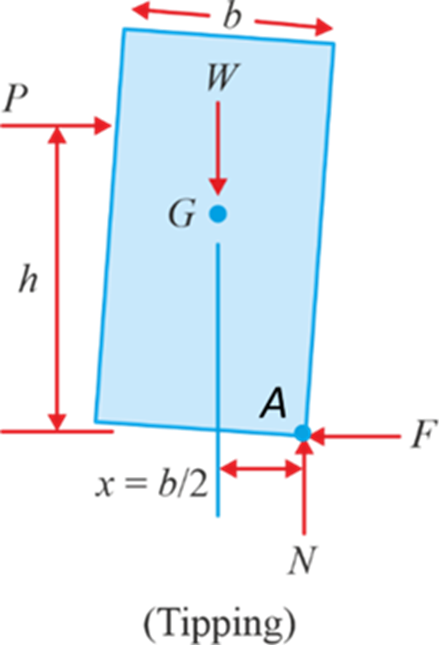 This rotational motion is known as toppling or tipping. At the time of tipping,
x
=
b
/2 and
N
is at the edge.
This rotational motion is known as toppling or tipping. At the time of tipping,
x
=
b
/2 and
N
is at the edge.
Effect of Friction
Friction has several significant effects, both positive and negative, in various aspects of our daily lives and engineering applications. Here are some key effects of friction:- Friction enables us to walk, hold objects, and move objects by providing necessary traction.
- It allows vehicles to grip the road, preventing skidding or sliding.
- Frictional forces are crucial in designing braking systems to ensure safe deceleration.
- Friction can cause wear and tear, leading to material loss and surface degradation.
- Friction forces lead to energy dissipation, resulting in the conversion of kinetic energy into heat.










