Lami’s Theorem, Definition, Proof, Limitation

Lami’s Theorem

Lami's Theorem, named after the French mathematician Bernard Lami, is a fundamental principle in engineering mechanics that relates the equilibrium of forces acting on a particle or a rigid body in a plane. It provides a concise and powerful method to analyze systems with concurrent forces.

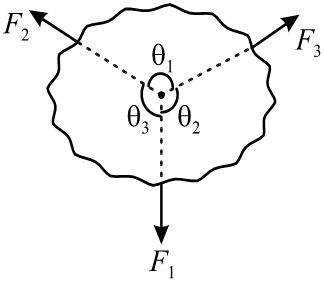
It states that, when a body under the action of three concurrent and coplanar forces of the same nature (i.e., pulling or pushing) is in equilibrium, then each force is proportional to the sine of the angle between the other two forces .

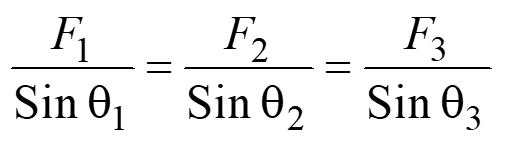
Proof of Lami's Theorem

If three coplanar and concurrent forces are acting on a particle (as shown in figure a) and are in equilibrium, then by the three-force triangle theorem we get a closed triangle (as shown in figure b).

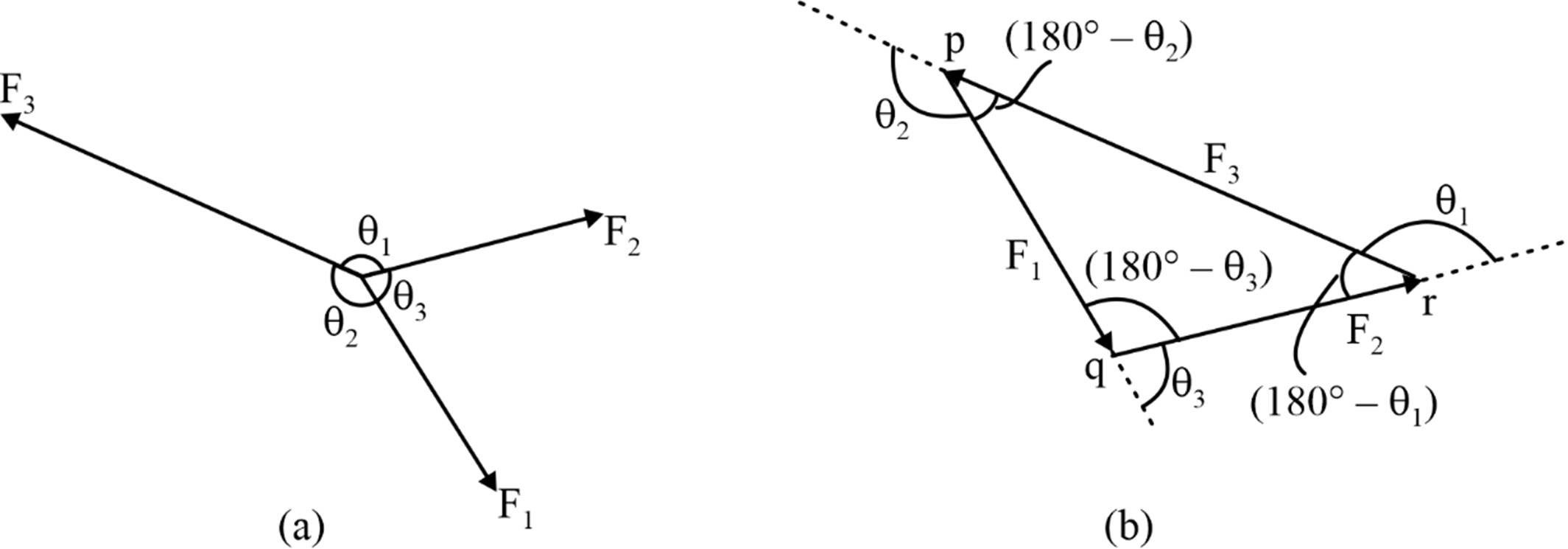
Applying sine rule in the triangle pqr, we have

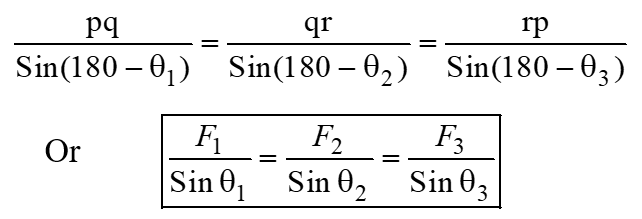
Limitations

• Applicable to three coplanar concurrent forces only.
• Forces must have the same nature (i.e., towards the point or away from the point).

Note points for using the Lami's Theorem

If the forces at the point of concurrency are not of the same nature, i.e., a combination of pulling and pushing forces, Lami's Theorem cannot be directly applied. In such cases, any one of the following approaches can be employed to analyze the equilibrium of forces:

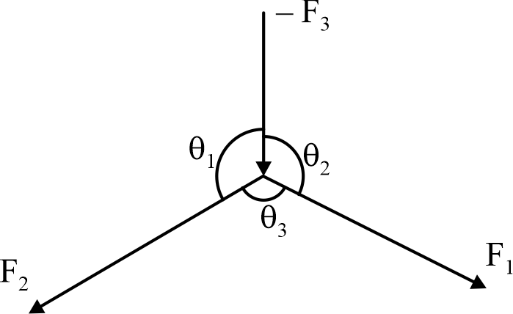
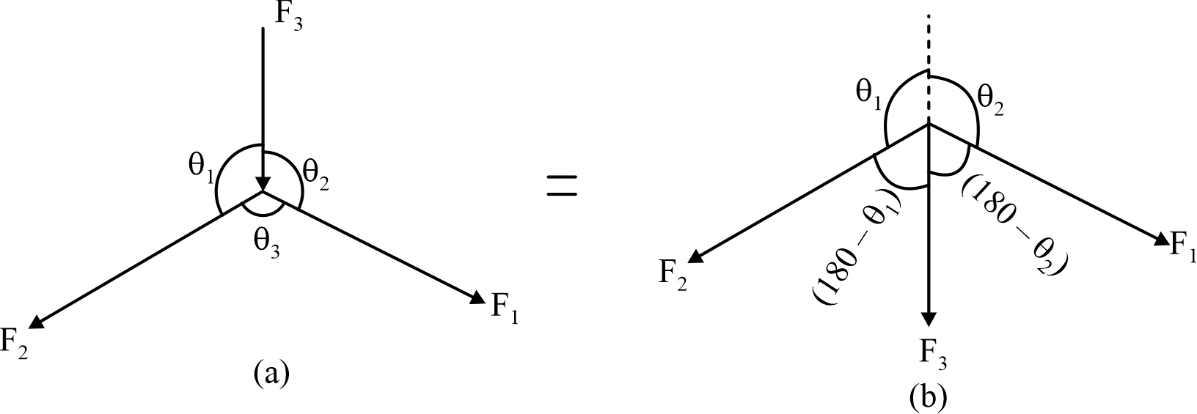
• In Figure a, forces F ₁ and F ₂ are pulling forces, while F ₃ is a pushing force. However, utilizing the principle of transmissibility, it is possible to transmit F ₃ to the other side of the point of concurrency, thereby converting all three forces into the same nature (i.e., pulling forces). By considering the resulting geometrical change in angles, Lami's Theorem can then be applied.
• Since force is a vector quantity, the introduction of a negative sign indicates an opposite sense or direction. Therefore, one can choose to represent the force F with a negative sign and subsequently apply Lami's Theorem, as illustrated in Figure.