
Virtual work method is a fundamental concept in engineering mechanics that allows us to analyze the equilibrium of structures and systems using the principle of virtual displacements. This method is widely used in various branches of engineering, including mechanical, civil, and aerospace, to analyze and design structures, machines, and mechanisms.
Traditionally, we break down rigid body equilibrium problems into smaller parts and solve using equations. Yet, this gets complex as systems grow, resulting in more parts and forces. Also, analyzing connected moving rigid bodies becomes difficult with standard equations. The traditional approach, although effective, can be time-consuming and lengthy. However, we have an alternative technique known as the Principle of Virtual Work, which offers distinct advantages, particularly when dealing with interconnected rigid bodies. This method allows us to determine unknowns directly without the need to disassemble the rigid bodies.
John Bernoulli formulated the principle of virtual work in 1717, which is also occasionally known as the unit-load method. A thorough understanding of the concepts of work, virtual work, and virtual displacement is crucial for grasping the essence of the "principle of virtual work."
-
Work is the measure of energy transfer that occurs when a force is applied to an object, causing it to move a certain distance in the direction of the force.
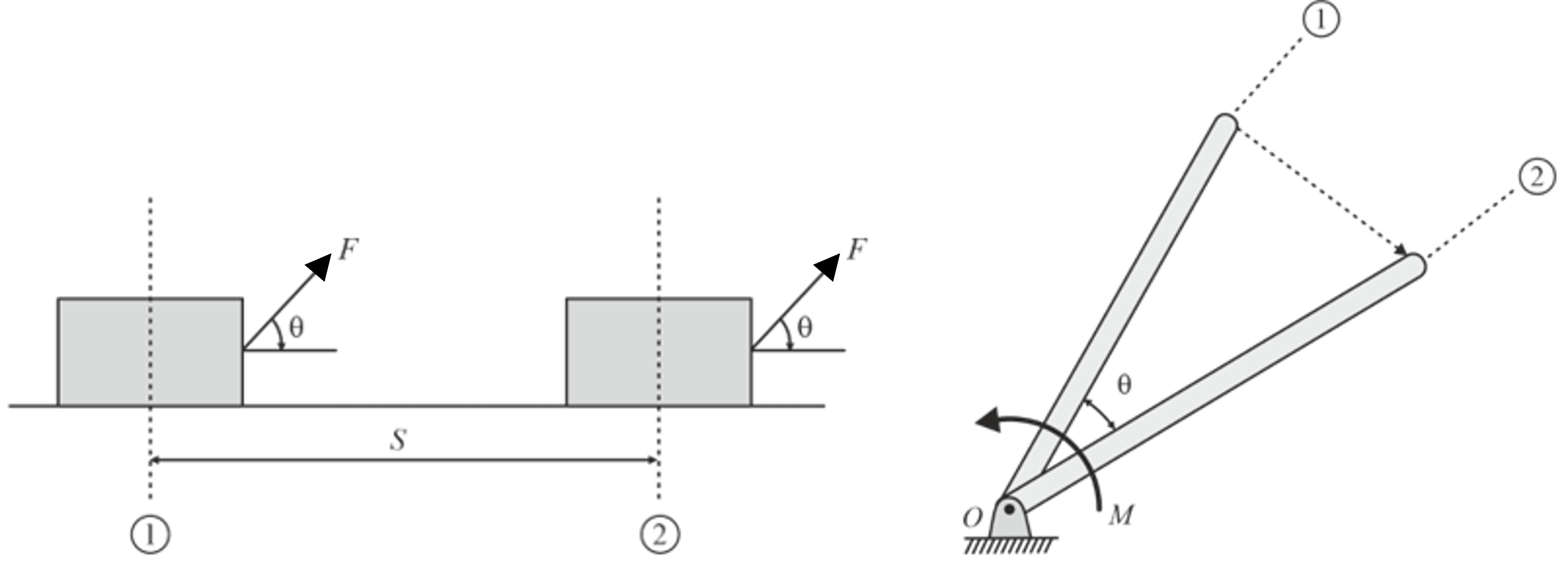
- A virtual displacement of a system can be described as "an extremely small movement of a point within a mechanical system that complies with the system's constraints, whether it occurs or not." Virtual displacement is assumed, not experienced, to compare potential equilibrium positions and determine the correct one.
- The work performed by a real force operating through a virtual displacement or a virtual force acting through a real displacement is known as virtual work.
Principle of Virtual Work
Virtual Work Method, also known as the Principle of Virtual Work, is a technique used to analyze the equilibrium of mechanical systems by considering the virtual displacements of the system under the influence of external forces and constraints. As per this principle, "
For a stable system of rigid bodies with a small virtual displacement satisfying geometric conditions, the algebraic sum of the virtual work done by the external active forces and couples is zero
." Mathematically, it can be expressed as:
![]()
Advantages of Virtual Work Method
- Conventional equilibrium equations between active forces can be formulated without the necessity of dismantling the system.
- Relationships between active forces may be determined without reference to the reactive forces.
- The equilibrium state of the system can be represented with a reduced number of unknown forces, simplifying the analysis process.
Procedure Steps for Analysis
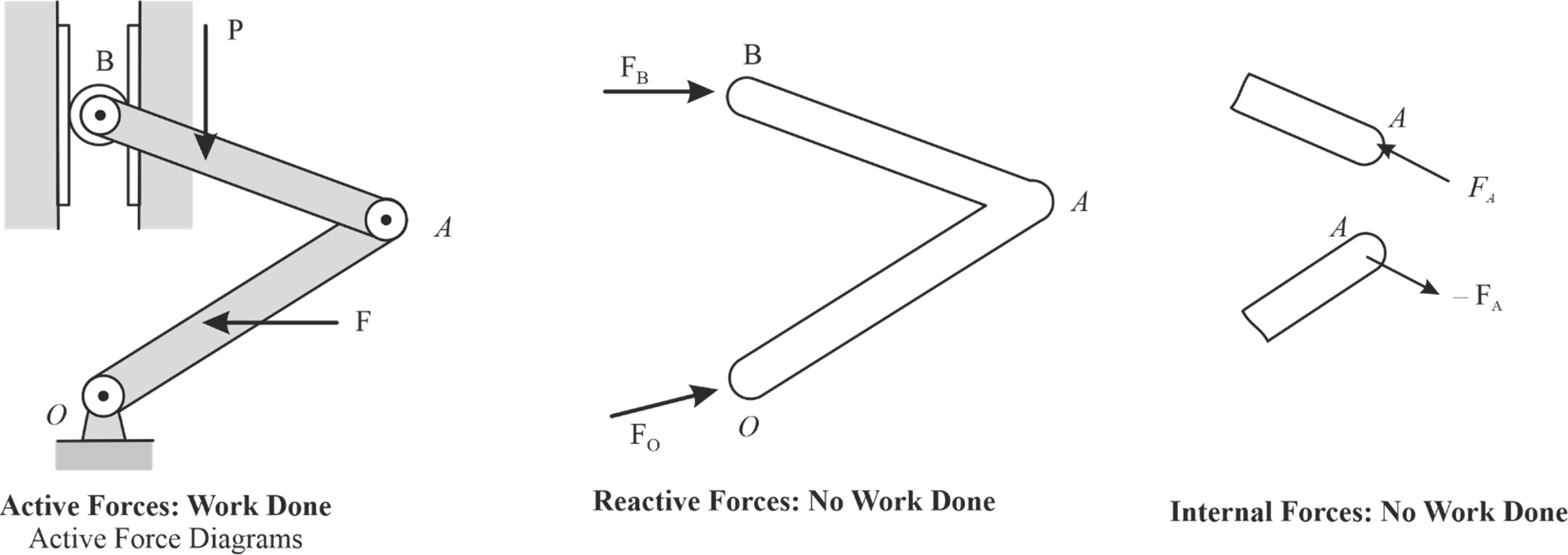
- Step 1: Construct an active-force diagram by illustrating the active forces on a free-body diagram of the entire system.
- Step 2: Apply virtual displacement(s) (rotation or deflection) to specific points of the system, ensuring that these displacements align with the geometry of the system and appropriately affect the points with unknown forces.
- Step 3: Evaluate the cumulative virtual work performed by all forces through their respective virtual displacements.
- Step 4: Account for the virtual work carried out by the reactions solely if the supporting elements themselves undergo virtual displacements.
- Step 5: Equate the sum of the virtual work to zero and solve for the unknown components of forces or moments.
Sign Convention
- The virtual work accomplished by a force or reaction is positive when its direction aligns with that of the virtual displacement.
- Negative virtual work arises when a force or reaction opposes the virtual displacement.
- Positive virtual work results from a moment in the same direction as the virtual rotation.
- Negative virtual work results from a moment in the direction opposite to the virtual rotation.
Example Problem
Find the magnitude of the necessary couple, denoted as M, that is essential to uphold the equilibrium of the mechanism.
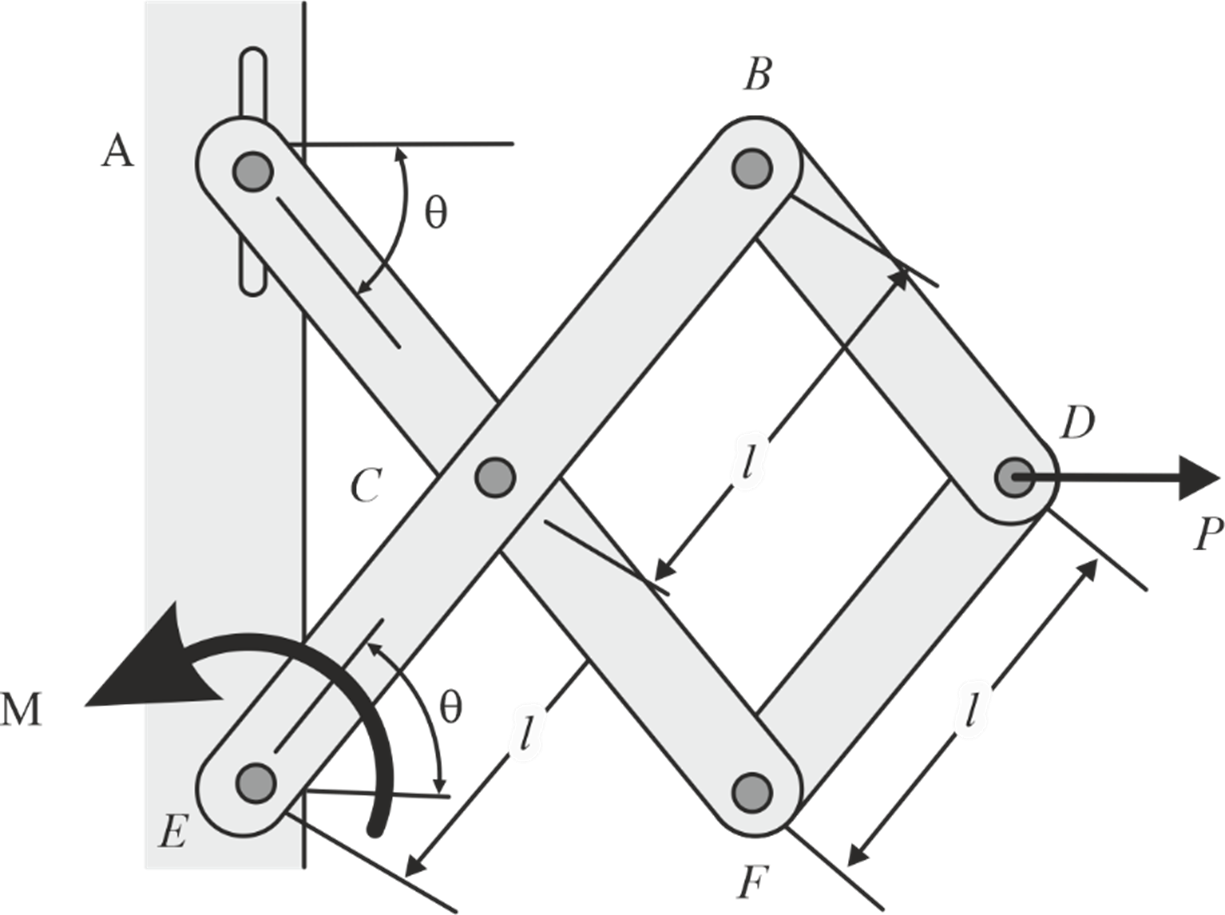
Solution: Apply a positive virtual increment to θ at E
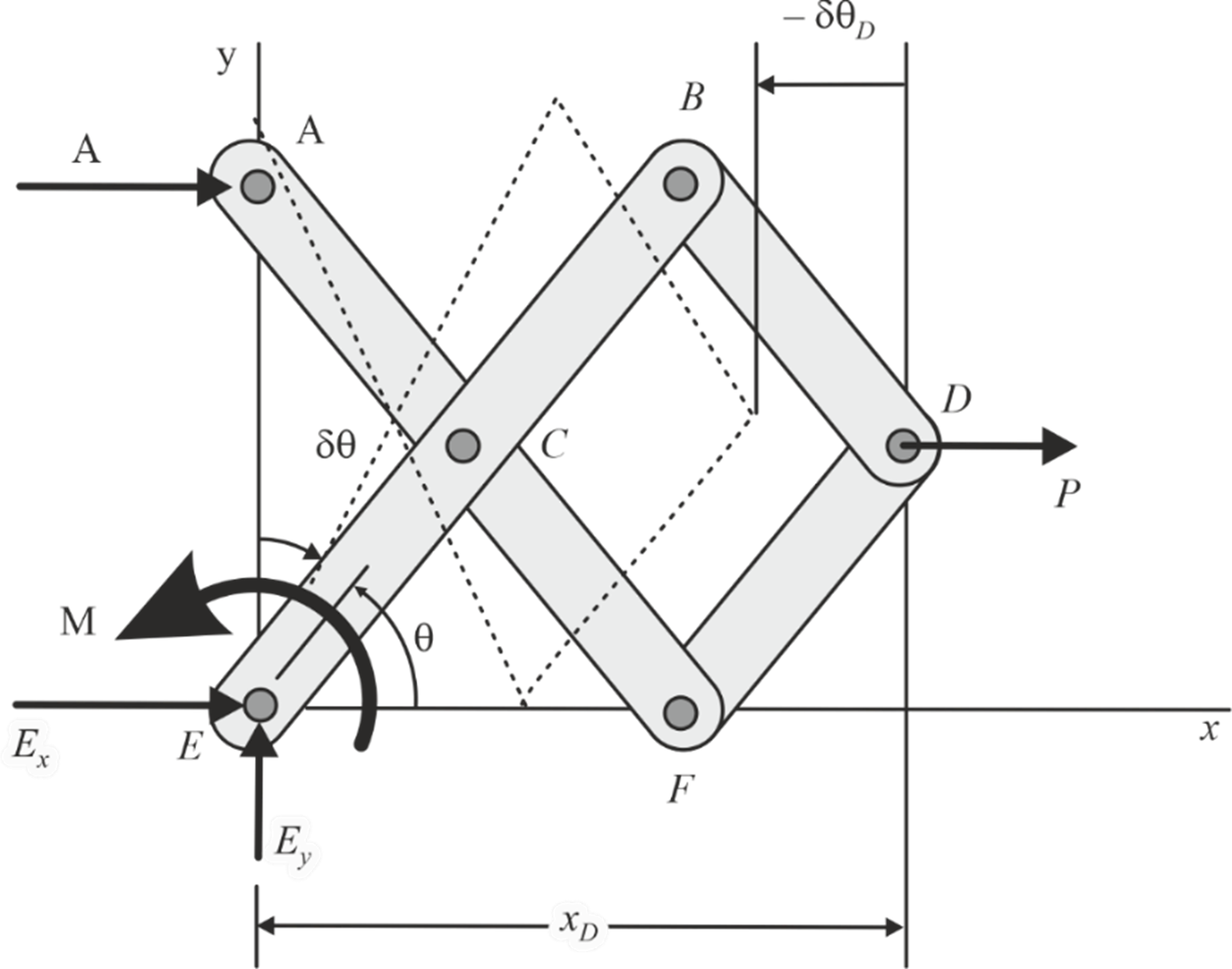
Apply the principle of virtual work.
δU = 0 = δU M + δU P
0 = Mδθ + Pδx D
δθ along positive θ ⇒ θ increases with δθ ⇒ + δθ
⇒ M and δθ have same sense, hence work done by moment M will be + Mδθ
For positive δθ, x D will decrease by δx D ⇒ –δx D
⇒ P and –δx D have opposite sense, hence work done by the force P will be –P(–δx D ) ⇒ + Pδx D
x D = 3l cosθ
⇒ δx D = – 3l sinθ dθ
dW = 0
⇒ Mδθ + P(– 3l sinθ δθ) = 0
⇒ M = Pl sin θ









