Death Well Or Rotor :
We will learn that “centripetal force” is another word for “force towards the center”. This force must originate from some external source such as gravitation, tension, friction, coulomb force, etc. Centripetal force is not a new kind of force, just as an “upward force” or a “downward force” is not a new kind of force. Circular motion is a two-dimensional motion or motion in a plane.
This plane may be horizontal, inclined, or vertical. But in most of the cases, this plane is horizontal. In circular motion, direction of velocity continuously keeps on changing. Therefore, even though speed is constant and velocity. keeps on changing. So, body is accelerated. Later we will see that this is a variable acceleration. So, we cannot apply the equations v = u + at etc. directly. Discussing centripetal and centrifugal force in detail with the help of Death motor.
Dynamics of Circular Motion :
In the above article, we have learnt that linear acceleration of a particle in circular motion has two.
components, tangential and radial (or centripetal). So, normally we resolve the forces acting on the
Particle In two directions :
Particle in two directions
:
(i)
tangential
(ii)
radial
In tangential direction, net force on the particle is
ma
t
and in radial direction net force is
ma
r
. In uniform circular motion, tangential acceleration is zero. Hence, net force in tangential direction is zero and in radial direction.
This net force (towards center) is also called
centripetal force
. In most of the cases plane of our uniform circular motion will be horizontal and one of the tangent is in vertical direction also. So, in this case we resolve the forces in:
(i)
Horizontal radial direction
(ii)
Vertical tangential direction
Centrifugal Force
Newton’s laws are valid only in inertial frames. In non-inertial frames a pseudo force −
ma
has to be applied. (
a
= acceleration of frame of reference). After applying the pseudo force one can apply Newton’s laws in their usual form. Now, suppose a frame of reference is rotating with constant angular velocity ω in a circle of radius ‘
r
’.
Then, it will become a non-inertial frame of acceleration
r
ω
2
towards the center. Now, if we observe an object of mass ‘
m
’ from this frame then a pseudo force of magnitude
mr
ω
2
will have to be applied to this object in a direction away from the center. This pseudo force is called the centrifugal force.
Example :
A particle of mass m is placed over a horizontal circular table rotating with an angular velocity ω about a vertical axis passing through its centre. The distance of the object from the axis is r. Find the force of friction
f
between the particle and the table.
Solutions :
Let us solve this problem from both frames. The one is a frame fixed on ground and
the other is a frame fixed on table itself.
From Frame of Reference Fixed on Ground (Inertial) :
Here,
N
will balance its weight and the force of friction
f
will provide the necessary centripetal force. Thus,
Ans.
f
=
mr
ω
2
From Frame of Reference Fixed on Table Itself (Non-inertial) :
In the free body diagram of particle with respect to table, in addition to above three forces (
N
,
mg
and
f
) a pseudo force of magnitude
mr
ω
2
will have to be applied in a direction away from the centre. But one thing should be clear that in this frame the particle is in equilibrium,
i.e.
N
will balance its weight in vertical direction while
f
will balance the pseudo force in horizontal direction.
or
f
=
mr
ω
2
Thus, we see that f comes out to be
mr
ω
2
from both the frames
In fact, centrifugal force is a sufficient pseudo force, only if we are analysing the particles at rest in a uniformly rotating frame. If we analyse the motion of a particle that moves in the rotating frame, we may have to assume other pseudo forces, together with the centrifugal force. Such forces are called the coriolis forces.
The coriolis force is perpendicular to the velocity of the particle and also perpendicular to the axis of rotation of the frame. Once again, we emphasize that all these pseudo forces, centrifugal or coriolis, are needed only if the working frame is rotating. If we work from an inertial frame, there is no need to apply any pseudo force. It is a common misconception among the beginners that centrifugal force acts on a particle because the particle goes on a circle. Centrifugal force acts (or is assumed to act) because we describe the particle from a rotating frame which is no inertial and still use Newton’s laws.
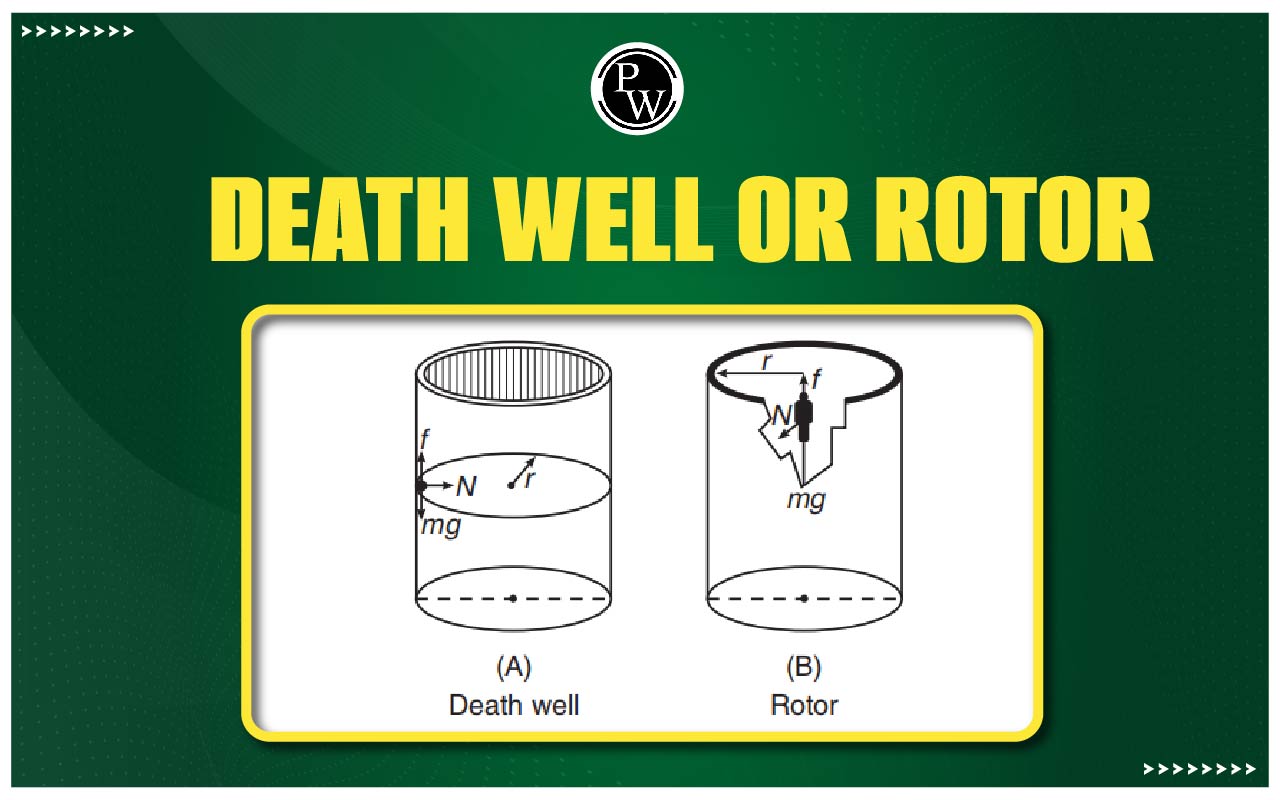
Death Well Or Rotor
Death Well Or Rotor :
In case of ‘death well’ a person drives a bicycle on a vertical surface of a large wooden well while in case of a rotor, at a certain angular speed of rotor a person hangs resting against the wall without any support from the bottom. In death well walls are at rest and person revolves while in case of rotor person is at rest and the walls rotate. In both cases, friction force balances the weight of person while reaction provides the centripetal force for circular motion, i.e.
