Important Questions for Class 10 Maths Chapter 12 Area Related to Circles
Important Questions For Class 10 Maths Chapter 12 Surface Area related to circles - Explore detailed answers and step by step solutions which will help you ace your Class 10 Math examination.
Neha Tanna17 Feb, 2024
Share
Important Questions for Class 10 Maths Chapter 12 Overview
There are several concepts and formulas in this chapter. Hence, we are providing Important Questions for Class 10 Maths Chapter 12. As a result, it is significant from the perspective of the exam since this chapter will comprise the majority of the objective-based questions. As they prepare for their exams, students can also review these crucial questions. We also offer NCERT Solutions to help students in achieving full marks.CBSE Class 10 Exam Pattern 2023-24
Important Questions for Class 10 Maths Chapter 12 Areas Related to Circles
Short Answer Type Questions
Below we have provided Important Questions for Class 10 Maths Chapter 12. Students are advised to practice these questions before their examination. 1. If the radius of a circle is 4.2 cm, compute its area and circumference.
Solution:
Area of a circle = πr
2
So, area = π(4.2)
2
= 55.44 cm
2
Circumference of a circle = 2πr
So, circumference = 2π(4.2) = 26.4 cm
2. What is the area of a circle whose circumference is 44 cm?
Solution:
Circumference of a circle = 2πr
From the question,
2πr = 44
Or, r = 22/π
Now, area of circle = πr
2
= π × (22/π)
2
So, area of circle = (22×22)/π = 154 cm
2
CBSE Class 10 Previous Year Question Papers
3. Calculate the area of a sector of angle 60°. Given, the circle has a radius of 6 cm.
Solution:
Given,
The angle of the sector = 60°
Using the formula,
The area of sector = (θ/360°) ×π r
2
= (60°/360°) × π r
2
cm
2
Or, area of the sector = 6 × 22/7 cm
2
= 132/7 cm
2
4. A chord subtends an angle of 90°at the centre of a circle whose radius is 20 cm. Compute the area of the corresponding major segment of the circle.
Solution:
Point to note:
Area of the sector = θ/360 × π × r
2
Base and height of the triangle formed will be = radius of the circle
Area of the minor segment = area of the sector – area of the triangle formed
Area of the major segment = area of the circle – area of the minor segment
Now,
Radius of circle = r = 20 cm and
Angle subtended = θ = 90°
Area of the sector = θ/360 × π × r
2
= 90/360 × 22/7 × 20
2
Or, area of the sector = 314.2 cm
2
Area of the triangle = ½ × base × height = ½ × 20 × 20 = 200 cm
2
Area of the minor segment = 314.2 – 200 = 114.2 cm
2
Area of the circle = π × r
2
= (22/7) × 20
2
= 1257.14
Area of the major segment = 1257.14 – 114.2 = 1142 .94 cm
2
So, the area of the corresponding major segment of the circle = 1142 .94 cm
2
5. A square is inscribed in a circle. Calculate the ratio of the area of the circle and the square.
Solution:
As the square is inscribed in a circle, a diagonal of the square will be = the diameter of the circle.
Let “r” be the radius of the circle and “d” be the length of each diagonal of the square.
We know,
Length of the diagonal of a square = side (s) × √2
So,
d = 2r
And, s × √2 = 2r
Or, s = √2r
We know, the area of the square = s
2
Thus, the area of the square = (√2r)
2
= 2r
2
Now, the area of the circle = π × r
2
∴ Area of the circle: area of the square = π × r
2
: 2r
2
= π : 2
So, the ratio of the area of the circle and the square is π : 2.
6. Find the area of the sector of a circle with a radius of 4cm and of angle 30°. Also, find the area of the corresponding major sector.
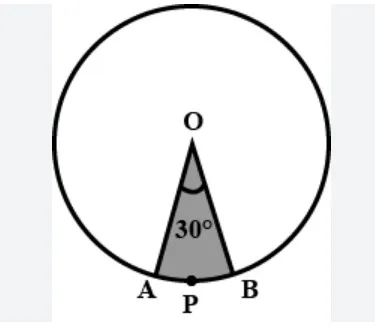Solution:
Radius = r = 4 cm, θ=30°
Area of sector = [𝜃/360] ×𝜋𝑟
2
= 30/360×3.14× (4)
2
= 1/12×3.14×4×4
= 1/3×3.14×4
= 12.56/3 cm
2
= 4.19 cm
2
Area of major sector = ((360 − θ)/360) ×𝜋𝑟
2
= ((360 − 30))/360×3.14× (4)
2
= 330/360×3.14×4×4
= 11/12×3.14×4×4
= 46.05 cm
2
7. Calculate the perimeter of an equilateral triangle if it inscribes a circle whose area is 154 cm
2
Solution:
Here, as the equilateral triangle is inscribed in a circle, the circle is an incircle.
Now, the radius of the incircle is given by,
r = Area of triangle/semi-perimeter
In the question, it is given that area of the incircle = 154 cm
2
So, π × r
2
= 154
Or, r = 7 cm
Now, assume the length of each arm of the equilateral triangle to be “x” cm
So, the semi-perimeter of the equilateral triangle = (3x/2) cm
And the area of the equilateral triangle = (√3/4) × x
2
We know, r = Area of triangle/semi-perimeter
So, r = [x
2
(√3/4)/ (3x/2)]
=> 7 = √3x/6
Or x = 42/√3
Multiply both numerator and denominator by √3
So, x = 42√3/3 = 14√3 cm
Now, the perimeter of an equilateral triangle will be = 3x = 3 × 14√3 = 72.7 cm.
Long Answer Type Questions
Below we have provided some Important Questions for Class 10 Maths Chapter 12, Students are advised to practice these questions before exams or better understanding of the concepts. Q.1: The cost of fencing a circular field at the rate of Rs. 24 per metre is Rs. 5280. The field is to be ploughed at the rate of Rs. 0.50 per m 2 . Find the cost of ploughing the field (Take π = 22/7). Solution: Length of the fence (in metres) = Total cost/Rate = 5280/24 = 220 So, the circumference of the field = 220 m If r metres is the radius of the field, then 2πr = 220 2 × (22/7) × r = 220 r = (220 × 7)/ (2 × 22) r = 35 Hence, the radius of the field = 35 m Area of the field = πr 2 = (22/7) × 35 × 35 = 22 × 5 × 35 m 2 = 3850 sq. m. Cost of ploughing 1 m 2 of the field = Rs. 0.50 So, the total cost of ploughing the field = 3850 × Rs. 0.50 = Rs. 1925 Q.2: The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour? Solution: The radius of car’s wheel = 80/2 = 40 cm (as D = 80 cm) So, the circumference of wheels = 2πr = 80 π cm Now, in one revolution, the distance covered = circumference of the wheel = 80 π cm It is given that the distance covered by the car in 1 hr = 66km Converting km into cm we get, Distance covered by the car in 1hr = (66 × 10 5 ) cm In 10 minutes, the distance covered will be = (66 × 10 5 × 10)/60 = 1100000 cm/s ∴ Distance covered by car = 11 × 10 5 cm Now, the no. of revolutions of the wheels = (Distance covered by the car/Circumference of the wheels) = 11 × 105 /80 π = 4375. Q.3: Find the area of the sector of a circle with a radius of 4 cm and of angle 30°. Also, find the area of the corresponding major sector (Use π = 3.14) Solution: Let OAPB be the sector. Area of the major sector = [(360 – θ)/ 360] × πr 2 = [(360 – 30)/360] × 3.14 × 4 × 4 = (330/360) × 3.14 × 16 = 46.05 cm 2 = 46.1 cm 2 (approx) Q.4: Find the area of the segment AYB shown in the figure, if the radius of the circle is 21 cm and ∠ AOB = 120°. (Use π = 22/7).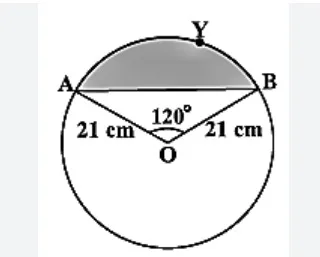
Solution:
Area of the segment AYB = Area of sector OAYB – Area of ∆ OAB …..(1)
Area of the sector OAYB = (120/360) × (22/7) × 21 × 21 = 462 cm
2
……(2)
Draw OM ⊥ AB.
OA = OB (radius)
Therefore, by RHS congruence, ∆ AMO ≅ ∆ BMO.
M is the mid-point of AB and ∠ AOM = ∠ BOM = (1/2) × 120° = 60°
Let OM = x cm
In triangle OMA,
OM/OA = cos 60°
x/21 = ½
x = 21/2
OM = 21/2 cm
Similarly,
AM/OA = sin 60°
AM/21 = √3/2
AM = 21√3/2 cm
AB = 2 AM = 2 (21√3/2) = 21√3 cm
Area of triangle OAB = (½) × AB × OM
= (½) × 21√3 × (21/2)
= (441/4)√3 cm
2
...(3)
From (1), (2) and (3),
Area of the segment AYB = [462 – (441/4) √3] cm
2
Q.5:
Find the area of the shaded design in the given figure, where ABCD is a square of 10 cm and semicircles are drawn with each side of the square as diameter. (Use π = 3.14).
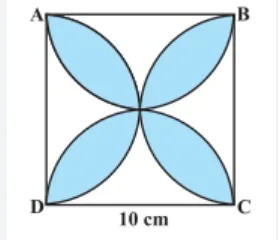Solution:
Let us assign I, II, III and IV for the unshaded regions.
Give that, side of square ABCD = 10 cm
The sides of a square are also the diameters of semicircles.
The radius of semicircle = 10/2 = 5 cm
Now, area of the region I +III = Area of square ABCD – Area of two semicircles of radius 5 cm
= (10)
2
– 2 × (½) π ×(5)
2
= 100 – 3.14 × 25
= 100 – 78.5
= 21.5 cm
2
Similarly,
Area of the region II + Iv = 21.5 cm
2
Area of the shaded region = Area of square ABCD – Area of the region (I + II + III + IV)
= 100 – 2× 21.5
= 100 – 43
= 57 cm
2
Q.6: A round table cover has six equal designs as shown in the figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs. 0.35 per cm
2
. (Use 3 = 1.7)
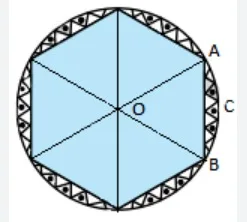Total number of equal designs = 6
∠AOB = 360°/6 = 60°
The radius of the cover = 28 cm
Cost of making design = Rs. 0.35 per cm
2
Since the two arms of the triangle are the radii of the circle and thus are equal, and one angle is 60°, ΔAOB is an equilateral triangle. So, its area will be √3/4 × a
2
Here, a = OA
∴ Area of equilateral ΔAOB = √3/4 × 28
2
= 333.2 cm
2
Area of sector ACB = (60°/360°) × π r
2
cm
2
= 410.66 cm
2
Area of a single design = area of sector ACB – Area of ΔAOB
= 410.66 cm
2
– 333.2 cm
2
= 77.46 cm
2
∴ Area of 6 designs = 6 × 77.46 cm
2
= 464.76 cm
2
So, the total cost of making design = 464.76 cm
2
× Rs. 0.35 per cm
2
= Rs. 162.66
Q.7: In the figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region (pink and yellow regions together).
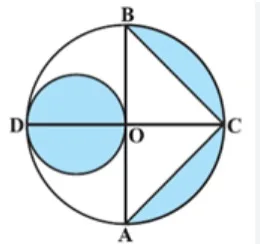Solution:
Radius of larger circle, R = 7 cm
Radius of smaller circle, r = 7/2 cm
Height of ΔBCA = OC = 7 cm
Base of ΔBCA = AB = 14 cm
Area of ΔBCA = 1/2 × AB × OC = 1/2 × 7 × 14 = 49 cm
2
Area of larger circle = πR
2
= 22/7 × 7
2
= 154 cm
2
Area of larger semicircle = 154/2 cm2 = 77 cm
2
Area of smaller circle = πr
2
= 22/7 × 7/2 × 7/2 = 77/2 cm
2
Area of the shaded region = Area of the larger circle – Area of a triangle – Area of larger semicircle + Area of the smaller circle
Area of the shaded region = (154 – 49 – 77 + 77/2) cm
2
= 66.5 cm
2
Q.8: In the figure, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (take π = 3.14)
Solution:
We know that the angle in the semicircle is the right angle.
Thus, ∠ACB = 9°
By Pythagoras theorem,
BC
2
+ AC
2
= AB
2
BC
2
= AB
2
– AC
2
= (13)
2
– (12)
2
= 169 – 144
= 25
⇒ BC = 5 cm
From the given,
Diameter of circle = AB = 13 cm
Radius of semicircle = AB/2 = 13/2 cm
Area of the shaded region = Area of the semicircle – Area of right triangle ABC
= (1/2)πr
2
– (1/2) × BC × AC
= (1/2) × 3.14 × (13/2) × (13/2) – (1/2) × 5 × 12
= 66.33 – 30
= 36.33 cm
2
Read More -
How to Increase Writing Speed for Board Exams: 5 Simple Tips
Benefits of Practicing Important Questions for Class 10 Maths Chapter 12
Below we have mentioned some benefits of practicing Important Questions for Class 10 Maths Chapter 12 Area related to Circles. These questions will help you understand the concepts better. Self-Assessment:- With the help of the offered solutions, students can evaluate their own responses, pinpoint areas for development, and correct errors.
- Frequent self-evaluation fosters ongoing learning and development as well as a sense of accountability.
- Students who successfully answer these questions will have developed effective time management skills, which are essential for finishing the exam in the allocated time.
- Students who are exposed to a range of questions are better able to manage their time effectively among various problem kinds.
- The variety of subjects covered in the questions enables students to review and solidify their comprehension of the chapter's most important ideas.
- Thorough revision via critical inquiry contributes to the strengthening of the knowledge base.
- With these crucial questions that are made to fit the format of the test, students can study for their Class 10 Maths exams in a focused and efficient manner.
- Students get familiar with the kinds of issues that are probably going to be on the test by practicing these questions.
| Important Questions for Class 10 Maths |
| Chapter 1 Real Numbers |
| Chapter 2 Polynomials |
| Chapter 3 Linear Equations In Two Variables |
| Chapter 4 Quadratic Equations |
| Chapter 5 Arithmetic Progression |
| Chapter 6 Triangles |
| Chapter 7 Coordinate Geometry |
| Chapter 8 Introduction to Trigonometry |
| Chapter 9 Applications of Trigonometry |
| Chapter 10 Circles |
| Chapter 11 Constructions |
| Chapter 12 Areas Related to Circles |
| Chapter 13 Surface Areas and Volumes |
| Chapter 14 Statistics |
| Chapter 15 Probability |
Important Questions For Class 10 Maths Chapter 12 FAQs
Which chapter is most important for class 10 maths?
Chapters on Real Numbers, Polynomials, and Quadratic Equations are critical, as they form the backbone of higher mathematical concepts.
How to score 95 in class 10?
Practice and revision are the keys to score 95 in class 10 or in any exam.
Can I crack boards in 1 month?
Yes, you can easily score 95+ in spite of simply one month of preparation. And, you simply have sufficient time to be prepared. The first thing for the best revision and preparation, having a better education, and a doubt solving partner is extremely crucial.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.