Physics Wallah

Important Questions for Class 10 Maths Chapter 7 Coordinate Geometry

Important Questions for Class 10 Maths Chapter 7 Coordinate Geometry - Explore detailed answers and step by step solutions which will help you ace your Class 10 Math examination.
authorImageNeha Tanna29 Mar, 2025
Share

Share

Important Questions for Class 10 Maths Chapter 7 Coordinate Geometry

 Important Questions for Class 10 Maths Chapter 7: At Physics Wallah, coordinate geometry is provided along with step-by-step solutions. It is recommended that students who are getting ready for the board exams practise these Important Questions for Class 10 Maths Chapter 7 to achieve good scores in the exam. Students can practise answering any problem from this chapter that may come up on the exam by answering these questions. Students' confidence will grow, and revision will be aided by answering these questions.

These concepts are crucial for board exams and are frequently asked in CBSE exam papers through short-answer, long-answer, and application-based questions. Practicing these important questions helps students strengthen their understanding, improve accuracy, and familiarize themselves with the exam pattern.

Important Questions for Class 10 Maths Chapter 7 Overview

The Important Questions for Class 10 Maths Chapter 7 have been provided by Physics Wallah in an easy-to-understand format for students to study. These questions are similar to the ones in the actual paper.

Since we completely adhere to the CBSE norms in this area, students will most likely find these questions common in their question paper. Students are introduced to coordinate geometry in mathematics in this chapter.

Important Questions for Class 10 Maths Chapter 7

By practicing the sums that are common and likely to be on the test, this article teaches students how to get ready for exams. Since mathematics is a difficult topic to study on your own, students can use the Important Questions for Class 10 Maths Chapter 7 to ace their exams. Students can complete the questions as part of their revision to help them prepare and do well on the Class 10 boards, which are very significant.

CBSE Important Questions for Class 10 Maths

Important Questions for Class 10 Maths Chapter 7 Coordinate Geometry

Coordinate Geometry

Coordinate geometry uses a variety of graphs and lines to illustrate how geometry and algebra are related. The following are some of the ideas this chapter discusses:

History of Coordinate Geometry

Rene Descartes, a French mathematician, is credited with developing coordinate geometry as the first technique to describe point locations. Later on in his investigation, he concluded that coordinate geometry might be used to find various curves and lines using equations.

CBSE Class 10 Notes

He was the pioneer in establishing the connection between algebra and geometry. The coordinate plane is referred to as the cartesian coordinate plane, and the coordinates of a point are called cartesian coordinates in honour of his highly valuable work.

Coordinates

The different places on the plane are known as coordinates. We can determine the precise location of the point by utilising the x- and y-axes. Locating anything is considerably simpler when utilising a grid system since all we have to do is figure out which cell—the point where the rows and columns intersect—that the point is in.

Coordinate Plane

Different points are positioned on a coordinate plane in coordinate geometry. Typically, there are two distinct scales: the y-axis, which is at a right angle to the plane, and the x-axis, which is perpendicular to it. The point of origin, which is often at point 0, is the location where the x and y axes converge. Coordinate geometry is a very basic geometry that locates a point on a plane using pairs of numbers.

Important Questions for Class 10 Maths Chapter 7 Coordinate Geometry

Q1: Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).

Solution:

Let P(x, y) be equidistant from the points A(7, 1) and B(3, 5). Then, AP = BP AP 2 = BP 2 Using the distance formula, (x – 7) 2 + (y – 1) 2 = (x – 3) 2 + (y – 5) 2 x 2 – 14x + 49 + y 2 – 2y + 1 = x 2 – 6x + 9 + y 2 – 10y + 25 x – y = 2 Hence, the relation between x and y is x – y = 2.

Q2: Find the distance of the point P (2, 3) from the x-axis.

Solution:

We know that, (x, y) = (2, 3) is a point on the Cartesian plane in the first quadrant. x = Perpendicular distance from y-axis y = Perpendicular distance from x-axis Therefore, the perpendicular distance from x-axis = y coordinate = 3. Q3: Find the coordinates of the points of trisection (i.e., points dividing into three equal parts) of the line segment joining the points A (2, – 2) and B (– 7, 4).

Solution:

Let P and Q be the points of trisection of AB, i.e., AP = PQ = QB. Class 10 Chapter 7 Imp ques.3 Therefore, P divides AB internally in the ratio 1: 2. Let (x 1 , y 1 ) = (2, -2) (x 2 , y 2 ) = (-7, 4) m 1 : m 2 = 1: 2 Therefore, the coordinates of P, by applying the section formula, 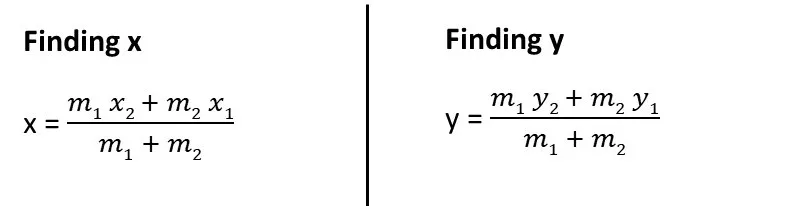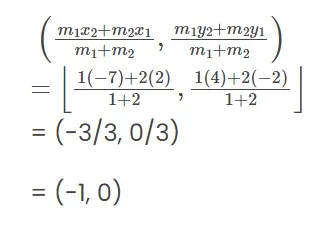Similarly, Q also divides AB internally in the ratio 2: 1. and the coordinates of Q by applying the section formula, 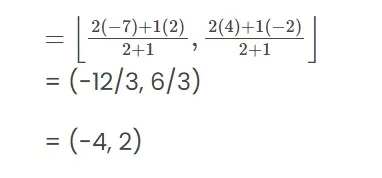Hence, the coordinates of the points of trisection of the line segment joining A and B are (–1, 0) and (– 4, 2).

Q4: Find the ratio in which the line segment joining the points (– 3, 10) and (6, – 8) is divided by (– 1, 6).

Solution:

Let the ratio in which the line segment joining ( -3, 10) and (6, -8) is divided by point ( -1, 6) be k:1. Therefore by section formula,
-1 = ( 6k-3)/(k+1) –k – 1 = 6k -3 7k = 2 k = 2/7 Hence, the required ratio is 2: 7.

Q5: Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.

Solution:

Let the vertices of the triangle be A(0, -1), B(2, 1) and C(0, 3). Let D, E, F be the mid-points of the sides of this triangle. Using the mid-point formula, coordinates of D, E, and F are: D = [(0+2)/2, (-1+1)/2] = (1, 0) E = [(0+0)/2, (-1+3)/2] = (0, 1) F = [(0+2)/2, (3+1)/2] = (1, 2) We know that, Area of triangle = ½ [x 1 (y 2 – y 3 ) + x 2 (y 3 – y 1 ) + x 3 (y 1 – y 2 )] Area of triangle DEF = ½ {(1(2 – 1) + 1(1 – 0) + 0(0 – 2)} = ½ (1 + 1) = 1 Area of triangle DEF = 1 sq.unit Area of triangle ABC = ½ {0(1 – 3) + 2(3 – (-1)) + 0(-1 – 1)} = ½ (8) = 4 Area of triangle ABC = 4 sq.units Hence, the ratio of the area of triangle DEF and ABC = 1 : 4.

Q6: Find the value of k if the points A(2, 3), B(4, k) and C(6, –3) are collinear.

Solution:

Given, A(2, 3)= (x 1 , y 1 ) B(4, k) = (x 2 , y 2 ) C(6, -3) = (x 3 , y 3 ) If the given points are collinear, the area of the triangle formed by them will be 0. ½ [x 1 (y 2 – y 3 ) + x 2 (y 3 – y 1 ) + x 3 (y 1 – y 2 )] = 0 ½ [2(k + 3) + 4(-3 -3) + 6(3 – k)] = 0 ½ [2k + 6 – 24 + 18 – 6k] = 0 ½ (-4k) = 0 4k = 0 k = 0

Q7: Name the type of triangle formed by the points A (–5, 6), B (–4, –2) and C (7, 5).

Solution:

The points are A (–5, 6), B (–4, –2) and C (7, 5). Using distance formula, d = √ ((x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ) AB = √((-4+5)² + (-2-6)²) = √(1+64) =√65 BC=√((7+4)² + (5+2)²) =√(121 + 49) =√170 AC=√((7+5)² + (5-6)²) =√144 + 1 =√145 Since all sides are of different lengths, ABC is a scalene triangle. Q8: Find the ratio in which the line x – 3y = 0 divides the line segment joining the points (-2, -5) and (6, 3). Find the coordinates of the point of intersection.
Solution:
 Let the given points be: A(-2, -5) = (x 1 , y 1 ) B(6, 3) = (x 2 , y 2 ) The line x – 3y = 0 divides the line segment joining the points A and B in the ratio k : 1. Using section formula, Point of division P(x, y) = [(kx 2 + x 1 )/(k + 1), (ky 2 + y 1 )/(k + 1)] x = (6k – 2)/(k + 1) and y = (3k – 5)/(k + 1) Here, the point of division lies on the line x – 3y = 0. Thus, [(6k – 2)/(k + 1)] – 3[(3k – 5)/(k + 1)] = 0 6k – 2 – 3(3k – 5) = 0 6k – 2 – 9k + 15 = 0 -3k + 13 = 0 -3k = -13 k = 13/3 Thus, the ratio in which the line x – 3y = 0 divides the line segment AB is 13 : 3. Therefore, x = [6(13/3) – 2]/ [(13/3) + 1] = (78 – 6)/(13 + 3) = 72/16 = 9/2 And y = [3(13/3) – 5]/ [(13/3) + 1] = (39 – 15)/(13 + 3) = 24/16 = 3/2 Therefore, the coordinates of the point of intersection = (9/2, 3/2). Q9: Find the area of triangle PQR formed by the points P(-5, 7), Q(-4, -5) and R(4, 5). Solution:
Given, P(-5, 7), Q(-4, -5) and R(4, 5) Let P(-5, 7) = (x 1 , y 1 ) Q(-4, -5) = (x 2 , y 2 ) R(4, 5) = (x 3 , y 3 ) Area of the triangle PQR = (½)|x 1 (y 2 – y 3 ) + x 2 (y 3 – y 1 ) + x 3 (y 1 – y 2 )| = (½) |-5(-5 – 5) + (-4)(5 – 7) + 4(7 + 5)| = (½) |-5(-10) -4(-2) + 4(12)| = (½) |50 + 8 + 48| = (½) × 106 = 53 Therefore, the area of triangle PQR is 53 sq. units. Q10: If the point C(-1, 2) divides internally the line segment joining A(2, 5) and B(x, y) in the ratio 3 : 4, find the coordinates of B. Solution:
 Given, C(-1, 2) divides internally the line segment joining A(2, 5) and B(x, y) in the ratio 3 : 4. Here, A(2, 5) = (x 1 , y 1 ) B(x, y) = (x 2 , y 2 ) m : n = 3 : 4 Using section formula, C(-1, 2) = [(mx 2 + nx 1 )/(m + n), (my 2 + ny 1 )/(m + n)] = [(3x + 8)/(3 + 4), (3y + 20)/(3 + 7)] By equating the corresponding coordinates, (3x + 8)/7 = -1 3x + 8 = -7 3x = -7 – 8 3x = -15 x = -5 And (3y + 20)/7 = 2 3y + 20 = 14 3y = 14 – 20 3y = -6 y = -2 Therefore, the coordinates of B(x, y) = (-5, -2). Q.11: Write the coordinates of a point on the x-axis which is equidistant from points A(-2, 0) and B(6, 0).
Solution: 
 Let P(x, 0) be a point on the x-axis. Given that point, P is equidistant from points A(-2, 0) and B(6, 0). AP = BP Squaring on both sides, (AP)² = (BP)² Using distance formula, (x + 2)² + (0 – 0)² = (x – 6)² + (0 – 0)² x² + 4x + 4 = x² – 12x + 36 4x + 12x = 36 – 4 16x = 32 x = 2 Therefore, the coordinates of a point on the x-axis = (2, 0). Q12: If A(-5, 7), B(-4, -5), C(-1, -6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.
Solution:
Given vertices of a quadrilateral are: A(-5, 7), B(-4, -5), C(-1, -6) and D(4, 5) The quadrilateral ABCD can be divided into two triangles ABD and BCD. Area of the triangle with vertices (x 1 , y 1 ), (x 2 , y 2 ), and (x 3 , y 3 ) = (½) |x 1 (y 2 – y 3 ) + x 2 (y 3 – y 1 ) + x 3 (y 1 – y 2 )| Area of triangle ABD = (½) |-5(-5 – 5) + (-4)(5 – 7) + 4(7 + 5)| = (½) |-5(-10) -4(-2) + 4(12)| = (½) |50 + 8 + 48| = (½) × 106 = 53 Area of triangle BCD = (½) |-4(-6 – 5) + (-1)(5 + 5) + 4(-5 + 6)| = (½) |-4(-11) -1(10) + 4(1)| = (½) |44 – 10 + 4| = (½) × 38 = 19 Therefore, the area of quadrilateral ABCD = Area of triangle ABD + Area of triangle BCD = 53 + 19 = 72 sq.units Q13: If A(-2, 1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram ABCD,
find the values of a and b. Hence, find the lengths of its sides. 
Solution:
Given vertices of a parallelogram ABCD are: A(-2, 1), B(a, 0), C(4, b) and D(1, 2) We know that the diagonals of a parallelogram bisect each other. So, midpoint of AC = midpoint of BD [(-2 + 4)/2, (1 + b)/2] = [(a + 1)/2, (0 + 2)/2] By equating the corresponding coordinates, 2/2 = (a + 1)/2 and (1 + b)/2 = 2/2 a + 1 = 2 and b + 1 = 2 a = 1 and b = 1 Therefore, a = 1 and b = 1. Let us find the lengths of sides of a parallelogram, i.e. AB, BC, CD and DA Using the distance formula, AB = √[(1 + 2)² + (0 – 1)²] = √(9 + 1) = √10 units BC = √[(4 – 1)² + (1 – 0)²] = √(9 + 1) = √10 units And CD = √10 and DA = √10 {the opposite sides of a parallelogram are parallel and equal} Hence, the length of each side of the parallelogram ABCD = √10 units.
Q14: Find the distance of a point P(x, y) from the origin.
Solution:
 Given, P(x, y) Coordinates of origin = O(0, 0) Let P(x, y) = (x 1 , y 1 ) O(0, 0) = (x 2 , y 2 ) Using distance formula, OP = √[(x 2 – x 1 )² + (y 2 – y 1 )²] = √[(x – 0)² + (y – 0)²] = √(x² + y²) Hence, the distance of the point P(x, y) from the origin is √(x² + y²) units.
Q15: Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, -3).
Hence, find m. 
Solution:
 Let P(4, m) divides the line segment joining the points A(2, 3) and B(6, -3) in the ratio k :
1. Here, P(4, m) = (x, y) A(2, 3) = (x  1 , y 1 ) B(6, -3) = (x 2 , y 2 ) Using section formula, p(x, y) = [(kx 2 + x 1 )/(k + 1), (ky 2 + y 1 )/(k + 1)] (4, m) = [(6k + 2)/(k + 1), (-3k + 3)/(k + 1)] By equating the x-coodinate, (6k + 2)/(k + 1) = 4 6k + 2 = 4k + 4 6k – 4k = 4 – 2 2k = 2 k = 1 Thus, the point P divides the line segment joining A and B in the ratio 1 : 1.
Now by equating the y-coodinate, (-3k + 3)/(k + 1) = m Substituting k = 1, [-3(1) + 3]/(1 + 1) = m m = (3 – 3)/2 m = 0
Important Questions for Class 10 Maths Chapter-wise
Important Questions Chapter 1 – Real Numbers
Important Questions Chapter 2 – Polynomials
Important Questions Chapter 3 – Linear Equations in Two Variables
Important Questions Chapter 4 – Quadratic Equations
Important Questions Chapter 5 – Arithmetic Progressions
Important Questions Chapter 6 – Triangles
Important Questions Chapter 7 – Coordinate Geometry
Important Questions Chapter 8 – Introduction to Trigonometry
Important Questions Chapter 9 – Some Applications of Trigonometry
Important Questions Chapter 10 – Circles
Important Questions Chapter 11 – Constructions
Important Questions Chapter 12 – Areas Related to Circles
Important Questions Chapter 13 – Surface Areas and Volume
Important Questions Chapter 14 – Statistics
Important Questions Chapter 15 – Probability

Benefits of Practicing Important Questions for Class 10 Maths Chapter 7

  • Covers Key Concepts: Focuses on essential topics like distance formula, section formula, and area of a triangle.

  • Aligned with CBSE class 10 Syllabus: Questions are based on the latest CBSE guidelines and exam pattern.

  • Enhances Problem-Solving Skills: Improves accuracy and speed in calculations.

  • Boosts Exam Confidence: Helps students get familiar with important question types.

  • Includes PYQs & class 10 Sample Papers: Provides exposure to previous years' questions for better exam preparation.

  • Improves Time Management: Regular practice helps in efficiently managing time during exams.

Important Questions for Class 10 Maths Chapter 7 FAQs

Why do we need coordinate geometry?

Coordinate geometry is needed to offer a connection between algebra and geometry with the use of graphs of lines and curves.

What is coordinate geometry used for in real life?

A coordinate system can be used to determine the position of any item from its starting point (known as the origin) to its current location. For example, we can measure the distance between the watch and the television from the other side of the room.

What is father of coordinate geometry?

The father of coordinate geometry is the French mathematician by the name of René Descartes. In the 17th century, he created the geometry of Cartesian coordinates.

What is the concept of coordinates?

Coordinates are a set of values which helps to show the exact position of a point in the coordinate plane.

Is coordinate geometry easy?

It is one of the easiest and most scoring topics of mathematics. The applications of coordinate geometry are spread through various fields of mathematics like trigonometry, calculus, dimensional geometry etc.
Popup Close ImagePopup Open Image
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Popup Image
CTA Image
07019243492
Check out these Related Articles
BlogImage
CLASS 10 EXAM
Share
NCERT Solutions for Class 10 Science Chapter 10 Light Reflection and Refraction
Read Full Story
22 Jul 2025, 12:12 pm
BlogImage
CLASS 10 EXAM
Share
NCERT Solutions for Class 10 English First Flight Chapter 2 PDF
Read Full Story
21 Jul 2025, 01:44 pm
BlogImage
CLASS 10 EXAM
Share
NCERT Solutions for Class 10 English First Flight Chapter 3 Question Answer
Read Full Story
19 Jul 2025, 11:13 am
BlogImage
CLASS 10 EXAM
Share
CBSE Class 10 Compartment Admit Card 2025, Check Expected Date
Read Full Story
8 Jul 2025, 04:43 pm
BlogImage
CLASS 10 EXAM
Share
NCERT Solutions for Class 10 Science Chapter 7 Control and Coordination
Read Full Story
5 Jul 2025, 02:36 pm
BlogImage
CLASS 10 EXAM
Share
CBSE Class 10 Compartment Exam Date 2025 OUT Download PDF
Read Full Story
28 Jun 2025, 11:20 am
BlogImage
CLASS 10 EXAM
Share
NCERT Solutions for Class 10 Science Chapter 6 Life Processes
Read Full Story
27 Jun 2025, 08:08 am
BlogImage
CLASS 10 EXAM
Share
CBSE Class 10 Board Exams Conducted Twice a Year from 2026 February Mandatory, May Optional
Read Full Story
26 Jun 2025, 12:38 pm
BlogImage
CLASS 10 EXAM
Share
CBSE Class 10th Toppers List 2025, Rank, Marks, Region Wise Stats other Details
Read Full Story
25 Jun 2025, 01:30 pm
Join 15 Million students on the app today!
Point IconLive & recorded classes available at ease
Point IconDashboard for progress tracking
Point IconMillions of practice questions at your fingertips
Download ButtonDownload Button
Banner Image
Banner Image
Free Learning Resources
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Privacy Policy
Terms of use
Copyright © 2025 Physicswallah Limited All rights reserved.