

Real Number Formula: A real number is a mathematical representation of a value that corresponds to something in the real world. These numbers are ubiquitous in our daily lives and serve various purposes. For instance, natural numbers are employed for counting objects, rational numbers are utilized to express fractions, irrational numbers come into play when calculating square roots, integers are used to measure temperature, and so forth. This diverse set of numbers collectively constitutes the realm of real numbers.
Definition of Real Numbers
Real numbers encompass both rational numbers (including integers and fractions) and irrational numbers. Numbers that fall outside the category of real numbers are known as non-real numbers or complex numbers. Examples of non-real numbers include √-1 (represented as "i" or the imaginary unit), complex numbers like 2 + 3i (with both real and imaginary components), and -i. These non-real numbers collectively constitute the set of complex numbers, denoted as C.
Also Check - Statistics Formula
Set of Real Numbers
The set of real numbers, represented as R, is a combination of two sets: the set of rational numbers (Q) and the set of irrational numbers. In mathematical notation, we express this as R = Q ∪ (Q̄). This means that real numbers encompass a wide range of number types, including natural numbers, whole numbers, integers, rational numbers, and irrational numbers. To provide a clearer picture, you can refer to the following table, which illustrates the various subsets of numbers that fall under the umbrella of real numbers.
| Number set | Is it a part of the set of real numbers? |
|---|---|
| Natural Numbers | ✅ |
| Whole Numbers | ✅ |
| Integers | ✅ |
| Rational Numbers | ✅ |
| Irrational Numbers | ✅ |
| Complex Numbers | ❌ |
List of Real Numbers
The set of real numbers is infinite because it encompasses a wide variety of number types, including whole numbers, natural numbers, integers, rational numbers, and irrational numbers. As it includes integers, it naturally encompasses negative numbers as well. Therefore, there is no specific starting or ending point for the list of real numbers; it extends infinitely in both directions along the number line.
Also Check - Circles Formula
Types of Real Numbers
Real numbers encompass both rational and irrational numbers. Consequently, there are no real numbers that fall outside these two categories. In other words, any number selected from the set of real numbers is either rational or irrational.
Rational Numbers:
Rational numbers are the numbers which can be expressed as fractions in the form p/q, where 'p' is the numerator and 'q' is the denominator, with 'q' not equal to zero. Rational numbers can include natural numbers, whole numbers, decimals, or integers. Examples of rational numbers include 1/2, -2/3, 0.5, and 0.333.
Download PDF Real Number Formula
Irrational Numbers:
Irrational numbers, on the other hand, are a subset of real numbers that cannot be represented as fractions in the form p/q, where 'p' and 'q' are integers and 'q' is not equal to zero (q≠0). For instance, π (pi) is an irrational number with an infinite decimal expansion (π = 3.14159265...). Other examples of irrational numbers include √2, -√7, and so forth.
In summary, real numbers consist of both rational and irrational numbers, covering the entire spectrum of numerical values, and any number from the set of real numbers can be categorized as either rational or irrational.
Also Check - Triangles Formula
Symbol of Real Numbers
Real numbers are denoted by the symbol R. Here's a list of symbols used to represent other types of numbers:
N: Natural numbers
W: Whole numbers
Z: Integers
Q: Rational numbers
Q̄: Irrational numbers
Subsets of Real Numbers
Real numbers encompass all numbers except complex numbers. Consequently, real numbers can be categorized into the following five subsets:
Rational Numbers: These are numbers that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. For example, 1/2, -3/4, and 7 are rational numbers because they can be written as fractions.
Irrational Numbers: These are numbers that cannot be expressed as a simple fraction of two integers. Irrational numbers have non-repeating, non-terminating decimal expansions. Examples of irrational numbers include √2 (the square root of 2), π (pi), and e (Euler's number).
Integers: Integers are whole numbers, both positive and negative, including zero. Examples include -3, -2, -1, 0, 1, 2, 3, and so on.
Whole Numbers: Whole numbers are non-negative integers, which means they include all positive integers and zero. Examples include 0, 1, 2, 3, and so on.
Natural Numbers: Natural numbers are positive integers, typically starting from 1. Examples include 1, 2, 3, 4, and so forth.
Real numbers are used extensively in various branches of mathematics, science, engineering, and everyday life to represent quantities, measurements, and values. They are essential for solving equations, performing calculations, and modeling real-world phenomena. The set of real numbers is denoted by the symbol ℝ .
Real Numbers Chart
Among the sets mentioned above, the sets N, W, and Z are subsets of Q. The following diagram illustrates the real number chart, which clarifies the relationships between these various types of numbers.
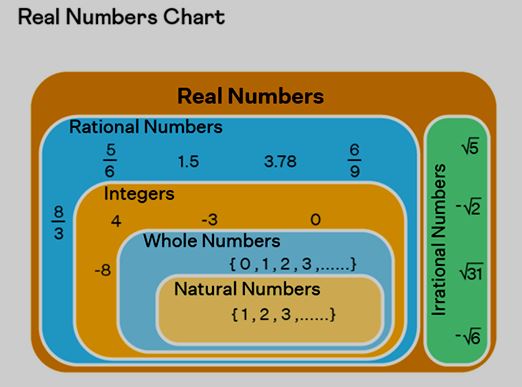
Properties of Real Numbers
Just like the set of natural numbers and integers, the set of real numbers also exhibits important algebraic properties. These properties are as follows:
Closure Property: The closure property asserts that the result of adding or multiplying two real numbers is always another real number. In mathematical terms, for any a and b belonging to the set of real numbers (R), both a + b and ab are also in R.
Associative Property: The associative property states that the sum or product of any three real numbers remains the same regardless of how the numbers are grouped. In other words, for a, b, and c in R, we have a + (b + c) = (a + b) + c and a × (b × c) = (a × b) × c.
Commutative Property: The commutative property asserts that the result of the addition or multiplication of two real numbers remains unchanged even if the order of the numbers is swapped. In R, for any a and b, we have a + b = b + a and a × b = b × a.
Distributive Property: Real numbers satisfy the distributive property, which is crucial for arithmetic operations. The distributive property of multiplication over addition is expressed as a × (b + c) = (a × b) + (a × c), and the distributive property of multiplication over subtraction is a × (b - c) = (a × b) - (a × c).
These properties make real numbers a fundamental and versatile mathematical system, underpinning various mathematical operations and calculations.
Also Check - Introduction to Euclid Formula
Real Numbers on a Number Line
A number line is a visual representation that allows us to depict numbers by assigning each number a unique point on the line. Here are the steps to represent real numbers on a number line:
Step 1: Begin by drawing a horizontal line with arrows at both ends. In the center of this line, mark the number 0, which is known as the origin.
Step 2: Create equal intervals on both sides of the origin, and label them with a consistent scale.
Step 3: Keep in mind that positive numbers are situated to the right of the origin, while negative numbers are located to the left of the origin.
Observe the numbers indicated on the number line, which includes real numbers like -5/2, 0, 3/2, and 2.
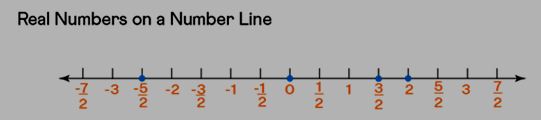
Difference Between Real Numbers and Integers
The primary distinction between real numbers and integers lies in the fact that real numbers encompass integers. In simpler terms, integers are a subset of real numbers. To clarify this difference, let's use the following table to illustrate the distinctions between real numbers and integers.
| Real Numbers | Integers |
|---|---|
| Real numbers include rational numbers, irrational numbers, whole numbers, and natural numbers. | Integers include negative numbers, positive numbers, and zero. |
| Examples of Real numbers: 1/2, -2/3, 0.5, √2 | Examples of Integers: -4, -3, 0, 1, 2 |
| The symbol used to denote real numbers is R. | The symbol used to denote integers is Z. |
| Decimal and fractions are considered to be real numbers. | Integers do not include decimals and fractions. |
Important Tips on Real Numbers
- All irrational numbers fall within the category of real numbers.
- All rational numbers are considered real numbers.
- Real numbers encompass all number types except for complex numbers.
- Every integer is a real number.
Examples Related to Real Numbers
Example 1: Tell the real numbers among the following: √6, -3, 3.15, -1/2, √-5.
Solution:
Among the given numbers, √-5 is a complex number, making it not a real number. The other numbers can be categorized as either rational or irrational, which are both subsets of real numbers. Thus, the real numbers in the list are √6, -3, 3.15, and -1/2.
Example 2: Fill in the blanks with respect to real numbers:
a.) Real numbers are denoted by the symbol R.
b.) Positive real numbers start from 0 or any positive number greater than 0.
Real Number Formula FAQs
Define the term Real Numbers.
Define the properties of Real Numbers.
Which numbers do not come under Real Numbers?
Does 0 come under the category of Real Number?












