
Introduction to Euclid Class 9 Math Formula : Euclid's Geometry, also referred to as Euclidean Geometry, encompasses the examination of flat and three-dimensional shapes, grounded in distinct axioms and theorems. The term "Geometry" derives from the Greek words 'geo', signifying 'earth', and 'metrein', signifying 'to measure'. Euclid's Geometry was introduced by the ancient Greek mathematician Euclid. He formulated a fundamental collection of principles and theorems that served as the foundation for a systematic exploration of geometry.
What Is Euclid's Geometry?
Euclid, often acknowledged as the Father of Geometry, introduced what is now referred to as Euclidean Geometry. This mathematical discipline evolved from the necessity of measuring land and was explored in diverse forms across ancient civilizations like Egypt, Babylonia, and India. The prominence of Euclid's geometry emerged when he synthesized all the fundamental concepts of geometry into a comprehensive work titled 'Elements'. This influential book encompassed definitions, axioms, theorems, and proofs concerning various geometric properties.
- A point has no parts.
- A line is a breadthless length.
- The ends of a line are points.
- A straight line is a line that lies evenly with the points on itself.
- A surface has a length and breadth only.
- The edges of a surface are lines.
- A plane surface is a surface that lies evenly with straight lines on itself .
In 'Elements', Euclid delved into aspects of shape, size, and spatial relationships of solid forms. He elaborated upon critical terminologies such as surfaces, straight or curved lines, and points. Notably, Euclid's comprehensive framework addressed the intricate characteristics of solid shapes, including their geometric properties, relationships, and classifications.
Also Check - Coordinate Geometry Formula
Definition of Euclid's Geometry
Euclid's geometry, also known as Euclidean geometry, revolves around the exploration of geometry using fundamental, undefined terms like points, lines, and planes in two-dimensional and three-dimensional spaces. This entails the investigation of both flat plane shapes and solid forms, elucidating the connections between these shapes through lines, points, and surfaces. Euclid introduced axioms and postulates in his renowned work "Elements" to establish a structured framework for defining these geometric entities.
Download PDF Introduction to Euclid Class 9 Maths Formula
Euclidean geometry encompasses two primary facets: plane geometry and solid geometry. Plane geometry pertains to shapes existing on a two-dimensional plane, while solid geometry delves into the properties of three-dimensional shapes. The provided table enumerates the theorems that Euclid demonstrated in his work.
| Plane Geometry | Theorem Proved |
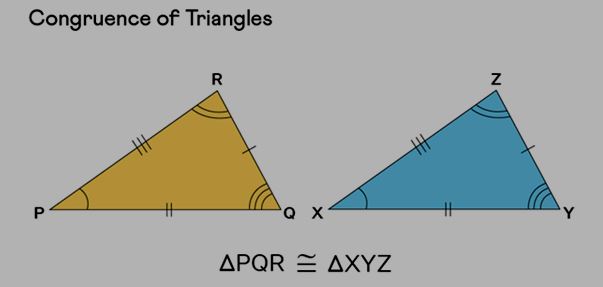
| Congruence of triangle | Two triangles are congruent if they are similar in shape and size. |
| Similarity of triangle | Two triangles are similar in shape but differ in size. |
| Areas | Area of a plane shape can be measured by comparing it with a unit square. |
| Pythagorean Theorem | Pythagorean theorem helps in calculating the distance in different situations for Geometric shapes. |
| Circles | Equal chord determines equal angles and vice versa in a circle. |
| Regular Polygons | Regular Polygons are equal in sides and angles. |
| Conic Section | Conic sections include Ellipse , Parabola , and Hyperbola. |
| Solid Geometry | Theorem Proved |
| Volume | Volume of a shape can be calculated. |
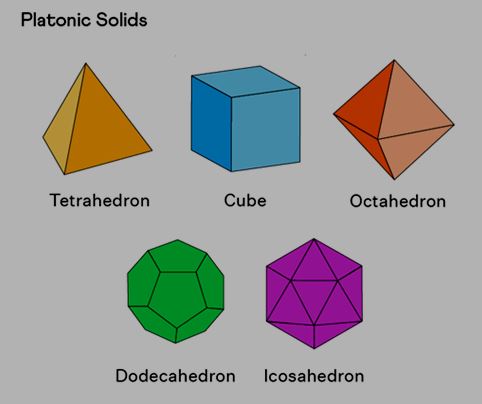
| Regular Solids | The existence of Platonic Solid |
Euclid's Axioms
Euclid's Axioms, also known as his common notions, consist of fundamental assumptions regarding self-evident truths that have not been proven. Within his renowned work "Elements," Euclid documented a set of axioms or common notions concerning geometric shapes. Let's delve into them:
Axiom 1: Things That Are Equal To The Same Thing Are Equal To One Another.
Given the scenario where the area of a rectangle matches that of a triangle, and the area of said triangle corresponds to the area of a square, we can utilize the initial axiom to deduce that the area of the triangle and the area of the square are identical. This can be understood through the application of the axiom "if p = q and q = r, then p = r." In simpler terms, if two equalities hold true sequentially, their equality extends to the third element as well.
Axiom 2: If Equals Are Added To Equals, The Wholes Are Equal.
Consider the line segment AB, where the lengths AP and QB are equal. Upon addition of the segment PQ to both sides, in accordance with axiom 2, we arrive at the equation AP + PQ = QB + PQ, which simplifies to AQ = PB.
Axiom 3: If Equals Are Subtracted From Equals, The Remainders Are Equal.
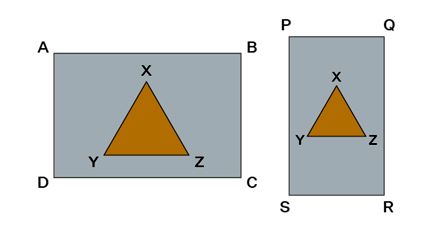
Take into account rectangles ABCD and PQRS, possessing equal areas. If triangle XYZ is subtracted from both of these rectangles, based on axiom 3, the areas of the remaining sections in both rectangles will also be equal.
Axiom 4: Things that Coincide With One Another Are Equal to One Another.
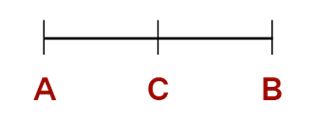
Consider line segment AB with C in the center. AC + CB coincides with the line segment AB. Thus by axiom 4, we can say that AC + CB = AB.
Axiom 5: The Whole Is Greater Than The Part.
Referring to the same diagram as mentioned earlier, where AC is a component of AB, axiom 5 asserts that AB is indeed greater than AC.
Axiom 6 And Axiom 7:
Things that are double of the same things are equal to one another. Things that are halves of the same things are equal to one another.
Also Check - Quadrilaterals Formula
Euclid's Postulate
When delving into Euclid's postulates, it's essential to familiarize ourselves with specific terms. Euclid outlines a progression involving solids, surfaces, lines, and points—this order being solids-surface-lines-points. Each step in this sequence represents a decrease in dimensions for the shape being discussed. Consequently, a solid constitutes a three-dimensional form, a surface represents a two-dimensional entity, a line characterizes a one-dimensional structure, and points encapsulate dimensions in their simplest form.
To elaborate, a surface pertains to something possessing length and breadth exclusively. On the other hand, a point possesses no dimensions, length, or breadth, essentially being the most basic form of a location.
Understanding these terms is pivotal for grasping Euclid's postulates better. There are five of Euclid's postulates that warrant our attention:
Postulate 1: A Straight Line Segment Can Be Drawn for Any Two Given Points.
This postulate demonstrates that a minimum of one straight line extends through two separate points, yet it doesn't imply that only one such line is possible. Observe the line presented below; there exists just one line, PQ, that traverses both points Q and P individually.
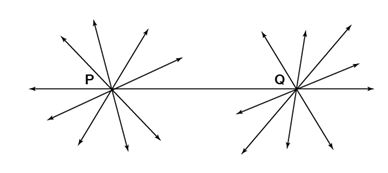
Postulate 2: A Line Segment Can Be Extended In Either Direction to Form A Line.
A line segment can be extended in either direction to form a line is the second postulate.
Postulate 3: To Describe A Circle With Any Center and Radius.
A circle is defined as a two-dimensional shape encompassing a collection of points that are uniformly distanced from a central point, and it can be illustrated using its center and radius. As per the third postulate, the essential form of a circle remains unaltered even as the radius varies. The aspect that does alter is the circle's magnitude or size.
Also Check - Linear Equation Formula
Postulate 4: All Right Angles Are Equal to One Another.
An angle that constitutes a 90° measurement remains consistent regardless of the lengths of its sides. Consequently, in line with postulate 4, all right angles exhibit equal measurements. However, this principle exclusively applies to right-angled triangles, distinguishing them from acute-angled and obtuse-angled triangles.
Postulate 5: If Two Lines Are Intersected By A Third In Such A Way That The Sum of The Inner Angles on One Side Is Less Than Two Right Angles, Then The Two Lines will Intersect Each Other on That Side if Produced Indefinitely.
When a third line intersects two other lines, if the summation of the interior angles is less than 180°, then upon extension, the two lines will converge on that particular side.
Introduction to Euclid Class 9 Math Formula FAQs
What is meant by Euclid’s Geometry?
Define Non-Euclid Geometry.
How many postulates are there in Euclid’s Geometry?
How many axioms are there in Euclid’s Geometry?










