
Circle Formula: Prior to delving into the intricacies of various circle formulas, let's take a moment to revisit the concept of a circle itself. A circle is characterized as the collection of points uniformly positioned at an identical distance from a specific point within a two-dimensional plane. This particular fixed point is referred to as the circle's center. The distance extending from the center of the circle to its periphery is termed the radius. With this fundamental understanding in place, we can now proceed to comprehend the array of circle formulas through the elucidation of solved examples.
Also Check - Factorization FormulaWhat Are All Circle Formulas?
A circle is a flat, two-dimensional shape composed of a collection of points situated at a constant distance (known as the radius) from a specific point referred to as the center or origin. The distance from the center to any point on the circle is referred to as the radius. To familiarize yourself with the fundamental components of a circle, namely the center, radius, and diameter, please refer to the illustration below.
 Also Check -
Line and Angles Formula
Also Check -
Line and Angles Formula
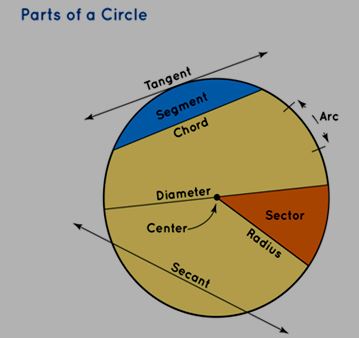
Parts of a Circle
The diagram presented below highlights the essential components of a circle, which are imperative for comprehending circles and their corresponding formulas.
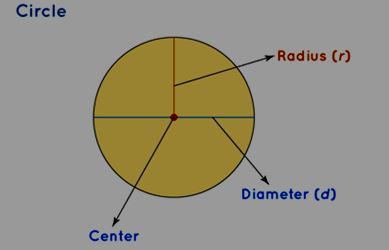
To comprehend the properties of a circle, it's crucial to familiarize ourselves with its various components. Here are several significant aspects of a circle explained below:
Circumference: Also known as the perimeter, the circumference of a circle represents the length of its outer boundary.
Radius of Circle: The radius is the distance extending from the circle's center to any point on its boundary. An infinite number of radii exist within a circle.
Diameter: A diameter is a straight line that passes through the center, connecting two points on the circle's boundary. Noteworthy characteristics of a diameter include:
- Passing through the center.
- Being a straight line.
- Touching the boundary at two distinct points situated opposite each other.
Chord of a Circle: A chord denotes a line segment that touches the circle at two distinct points on its boundary. The longest chord is the diameter, which divides the circle into two equal parts by passing through the center.
Tangent: A tangent is a straight line that touches the circle at a single point, while remaining outside the circle.
Secant: A secant is a line intersecting the circle at two points along its circumference.
Arc of a Circle: An arc is a curved portion of the circle's circumference, representing a segment or part of it.
Segment in a Circle: This refers to the area enclosed by a chord and the corresponding arc within a circle. Two types of segments exist the minor segment and the major segment.
A sector of a Circle: A sector is a region enclosed by two radii and the corresponding arc in a circle. Similar to segments, there are two types of sectors: the minor sector and the major sector.
 Also Check -
Squares and Square Roots Formula
Also Check -
Squares and Square Roots Formula
Properties of Circle
Let's progress and delve into some intriguing attributes that distinguish circles from other geometric shapes. Here's a compilation of circle properties:
- A circle is a closed two-dimensional figure distinguished by its singular curved surface.
- Circles can be termed congruent if their radii are identical in length.
- Equal chords within a circle are consistently equidistant from its center.
- The perpendicular bisector of a chord traverses through the circle's center.
- When two circles intersect, the line linking their intersection points stands perpendicular to the line linking their centers.
- Tangents are drawn at the extremities of a diameter exhibit parallelism to each other.
Circle Formulas
Numerous formulas are associated with circles. Here's a compilation of fundamental circle formulas:
- Area of a Circle Formula: The area occupied by a circle is determined by its radius → Area = πr², where 'r' is the radius and π ≈ 3.14.
- Circumference of a Circle Formula : The aggregate length of a circle's boundary is given by → Circumference = 2πr, where 'r' is the radius and π ≈ 3.14.
- Arc Length Formula : An arc, a segment of the circumference, can be characterized by its length = θ × r. Here, θ is measured in radians, and 'r' is the radius.
- Area of a Sector Formula : When a sector forms an angle θ (in radians) at the center, its area = (θ × r²) ÷ 2. Here, θ is in radians.
- Length of Chord Formula : If the chord's angle at the center and the radius are known, chord length = 2r sin(θ/2). Here, θ is in radians.
- Area of Segment Formula : A segment is the area enclosed by a chord and its corresponding arc. Area of a segment = (r² * (θ - sinθ)) ÷ 2. Here, θ is in radians.
| Parameters | Circle Formulas |
| Diameter of a circle formula | D = 2 × r |
| Circumference of a circle formula | C = 2 × π × |
| Area of a circle formula | A = π × r 2 |
Circle Formula FAQs
What is the formula for calculating the perimeter of a semicircle?
What is the formula for calculating the diameter of a circle?
What formula is used to calculate the perimeter of a circle?
How can the radius be calculated using the circle formula?










